Сравнительная характеристика статистических критериев Возможности и ограничения параметрических и непараметрических критериев

ПАРАМЕТРИЧЕСКИЕ	НЕПАРАМЕТРИЧЕСКИЕ
1. Позволяют прямо оценить различия в средних, полученных в 2-х выборках (t-критерий Стьюдента)	Позволяют оценить лишь средние тенденции, например, ответить на вопрос, чаще ли в выборке А встречаются более высокие, а в выборке Б – более низкие значения признака (U-критерий Манна-Уитни и др.)
2. Позволяют прямо оценить различия в дисперсиях (F-критерий Фишера)	Позволяют оценить лишь различия в диапазонах вариативности признака (критерий φ-корелляции Пирсона)
3. Позволяют выявить тенденции изменения признака при переходе от условия к условию (дисперсионный однофакторный анализ), но лишь при условии нормального распределения признака	Позволяют выявить тенденции изменения признака при переходе от условия к условию при любом распределении признака (критерий тенденций S (Джонкира)
4. Позволяют оценить взаимодействие 2-х и более факторов в их влиянии на изменения признака (двухфакторный дисперсионный анализ)	Эта возможность отсутствует
5. Экспериментальные данные должны отвечать 2-м, а иногда 3-м условиям: а) значения признака измерены по интервальной шкале; б) распределение признака является нормальным; в) в дисперсионном анализе должно соблюдаться требование равенства дисперсий в ячейках комплекса	Экспериментальные данные могут не отвечать ни одному из этих условий: а) значения признака могут быть представлены в любой шкале; б) распределение признака может быть любым и совпадение его с каким-либо теоретическим законом распределения необязательно и не нуждается в проверке; в) требование равенств дисперсий отсутствует
6. Математические расчёты довольно сложны	Математические расчёты по большей части просты и занимают мало времени (за исключением критериев χ2 и φ)
7. Если условия, перечисленные в п.5, выполняются, параметрические критерии оказываются несколько более мощными, чем непараметрические	Если условия, перечисленные в п.5, не выполняются, непараметрические критерии оказываются более мощными, чем параметрические, так как они менее чувствительны к «шумам»

• 2. t-КРИТЕРИЙ СТЬЮДЕНТА

Сравнение двух выборок по признаку, измеренному в метрической шкале, обычно предполагает сравнение средних значений с использованием параметрического t-критерия Стьюдента.

Следует различать 3 ситуации по соотношению выборок между собой:

1) случай независимых выборок (измерений признака) /двухвыборочный/;

2) случай зависимых выборок /двухвыборочный/;

3) случай сравнения одного среднего значения с заданной величино (t-критерий Стьюдента для одной выборки /одновыборочный/).

t-критерий Стьюдента – многофункциональный параметрический критерий различия, позволяющий оценивать различия выборок на основании их средних значений. Может применяться для оценки различия в зависимых и независимых выборках равного и неравного размера. Может применяться по отношению к данным, полученным в интервальной шкале и шкале отношений. Ограничений по объёму выборки нет, распределение данных должно быть близко к нормальному закону, дисперсии обеих выборок должны быть равными или, по крайней мере, не должны сильно различаться.

В общем случае формула для расчёта по t-критерию Стьюдента для двух выборок такова:

В случае зависимых, равных по объёму выборок формула упрощается:

где – стандартное отклонение разностей соответствующих значений первой и второй выборки.

t-критерий Стьюдента также может применяться при проверке гипотезы об отличии среднего значения выборки от некоторого значения (насколько достоверно больше или меньше его). Формула для расчёта эмпирического значения в этом случае выглядит так:

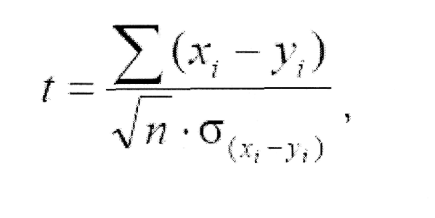
• где – стандартное отклонение разностей соответствующих значений первой и второй выборки.

t-критерий Стьюдента также может применяться при проверке гипотезы об отличии среднего значения выборки от некоторого значения (насколько достоверно больше или меньше его). Формула для расчёта эмпирического значения в этом случае выглядит так:

где А - значение, для которого проверяется гипотеза, п - численность выборки, по отношению к которой проверяется допущение об отличии от значения А. Число степеней свободы для данных формул равно df = п-1.

18. Параметрические критерии. F-критерий Фишера.

К параметрическим методам относится и сравнение дисперсий двух выборок по F-критерию Фишера. Иногда этот метод приводит к ценным содержательным выводам, а в случае сравнения средних для независимых выборок сравнение дисперсий является обязательной процедурой.

Параметрический критерий различия, основан на сравнении дисперсий 2-х выборок и вычисления величины их отношения. Применяется по отношению к данным, полученным в интервальной шкале и шкале отношений. Ограничений по числу испытуемых нет, сравниваемые выборки должны быть распределены по нормальному закону.

Вычисляются дисперсии обеих выборок, после чего находится критерий F_э путём деления бóльшей по значению дисперсии на меньшую.

Критические значения F_кр находятся по специальным таблицам на основании значений степеней свободы большей и меньшей выборки (соответственно df₁ = п₁ -1 и df₂ = п₂ -1), после чего они сравниваются с величиной F_э и делается вывод о наличии или отсутствии различий между этими выборками.

Альтернатива методу: критерий Ливена (Levene’s Test), применение которого не требует проверки предположения о нормальности (используется в программе SPSS).

19. Условия применения непараметрических критериев. Критерий U-Манна-Уитни.

Почти каждый параметрический метод сравнения средних может быть при необходимости заменён своим непараметрическим аналогом или сочетанием непараметрических методов.

Непараметрические методы заметно проще в вычислительном отношении, чем их параметрические аналоги. До недавнего прошлого простота вычислений имела существенное значение при обработке данных «вручную». Но, компьютерная обработка снимает проблему сложности вычислений. Поэтому при выборе между параметрическими и непараметрическими методами следует исходить из свойств самих данных!

Непараметрические аналоги параметрических методов сравнения выборок применяются в случаях, когда не выполняются основные предположения, лежащие в основе параметрических методов сравнения средних значений.

При решении вопроса о выборе параметрического или непараметрического метода сравнения необходимо иметь в виду, что параметрические методы обладают заведомо большей чувствительностью, чем их непараметрические аналоги. Поэтому исходной ситуацией является выбор параметрического метода. Решение о применении непараметрического метода становится оправданным, если не выполняются исходные предположения, лежащие в основе применения параметрического метода.