
- •«Математические методы в психологии»
- •Четыре типа измерительных шкал.
- •Порядковая (ранговая) шкала
- •Интервальная шкала
- •Шкала отношений (абсолютная шкала)
- •1) Правило порядка ранжирования
- •2) Правило связанных рангов.
- •Случайная выборка
- •1.2 Стратифицированная (расслоенная) выборка.
- •1.3 Групповая выборка (кластерная, гнездовая)
- •1.4 Простая выборка
- •1.5 Зависимые и независимые выборки
- •2) Однородность генеральной совокупности
- •3) Вероятность ошибки (уровень статистической значимости) p.
- •4) Предельная ошибка репрезентативности выборки («ошибка выборки»)
- •6) Совместное использование ошибки репрезентативности выборки и дисперсии признака
- •1) Мода;
- •2) Среднее арифметическое значение;
- •3) Медиана.
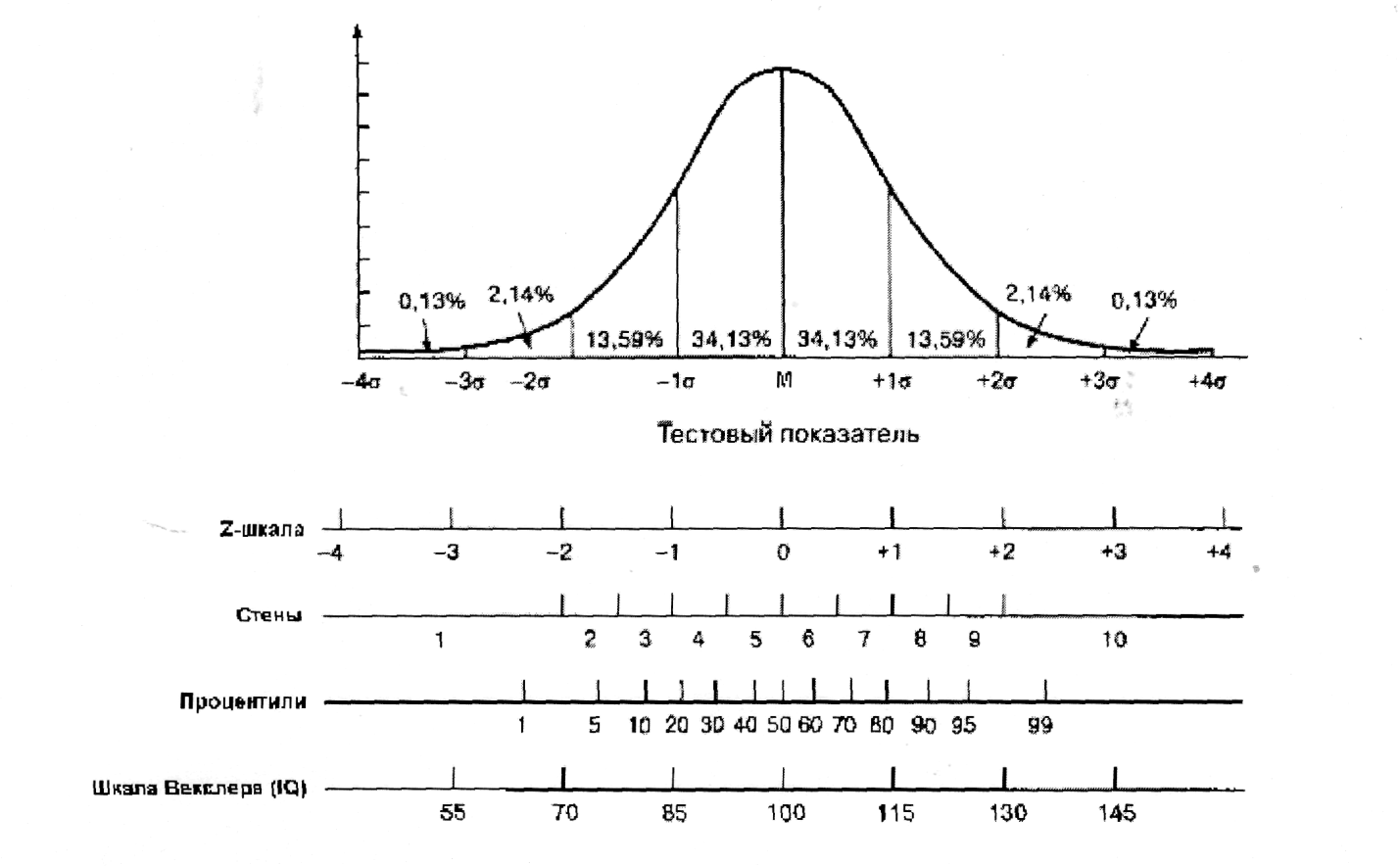
- •Чаще всего сырые баллы переводят в следующие шкалы: - стены,
- •- Процентили.
- •Соотношение нормального распределения и показателей различных стандартизированных шкал.
- •Параметрические и непараметрические показатели
- •1) Параметрические;
- •2) Непараметрические.
- •Задачи исследования и используемые для их решения методы
- •Соотношение р- уровня и статистической значимости
- •Этапы проверки статистических гипотез
- •Степени свободы
- •Сравнительная характеристика статистических критериев Возможности и ограничения параметрических и непараметрических критериев
- •Условия, когда применение непараметрических методов является оправданным:
- •1) Есть основания считать, что распределение значений признака в генеральной совокупности не соответствует нормальному закону;
- •2) Есть сомнения в нормальности распределения признака в генеральной совокупности, но выборка слишком мала, чтобы по выборочному распределению судить о распределении в генеральной совокупности;
- •Определение значимости корреляции
- •1) А связано с в;
- •2) А предшествует в (направление связи от а к в);
- •3) Отношения между а и в не связаны с их отношениями с с (в деле не
Соотношение нормального распределения и показателей различных стандартизированных шкал.
14. Классификация задач исследования и методов их решения. Параметрические и непараметрические критерии.
Параметрические и непараметрические показатели
Все критерии различий условно подразделены на 2 группы:
1) Параметрические;
2) Непараметрические.
Критерий является параметрическим, если он основан на определённом типе распределения генеральной совокупности (нормальном) или использует определённые параметры этой совокупности (среднее, дисперсию, стандартное отклонение и пр.).
Если критерий «свободен» от распределения и не использует вышеуказанные параметры, он называется непараметрическим.
Обычно при вычислении вручную непараметрические критерии являются значительно менее трудоёмкими, чем параметрические.
При нормальном распределении параметрические критерии обладают большей мощностью, т.е. они способны с большей достоверностью доказывать или опровергать изучаемую взаимосвязь явлений. Однако, как показывает практика, большее число получаемых в экспериментах данных не распределено по нормальному закону, и применение к ним параметрических методов анализа может привести к ошибкам в статистических выводах.
В этом случае значения параметрических показателей просто не будут иметь смысла, поскольку они были получены без соблюдения необходимых правил.
В этом случае более мощными оказываются непараметрические критерии. Непараметрические критерии выявляют значимые различия даже в том случае, если распределение близко к нормальному, однако менее значимые различия не поддаются выявлению с их помощь.
Для
каждой из задач применяются соответствующие
статистические критерии. Е.В. Сидоренко
предлагает следующую классификацию
задач и методов их статистического
решения (табл. 1.):
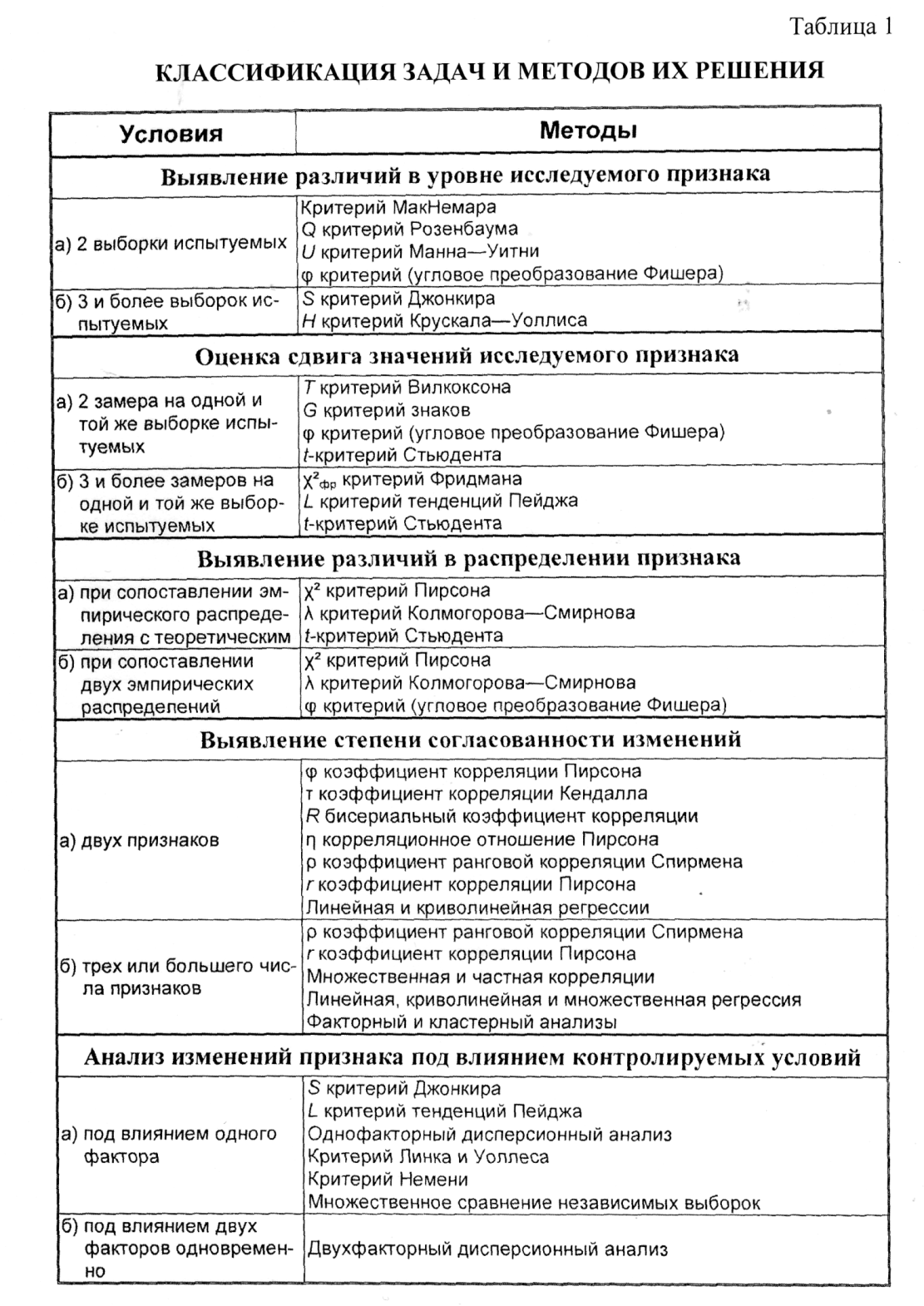
Задачи исследования и используемые для их решения методы
Проверка статистических гипотез в большинстве исследований подразумевает решение одной из 3 основных задач:
1. Выявление наличия различия между группами - когда целью становится констатация различия групп по определённому признаку (без подробного анализа того, в чём состоит различие).
Поскольку критерий различия между группами известен, необходимо лишь показать что в изучаемых группах он принимает различные значения, и доказать это статистически.
2. Выявление степени различия между группами - когда различия по определённому признаку определяются количественно. Могут сравниваться либо две различные группы (независимые выборки), либо одна и та же группа до и после эксперимента (зависимые выборки).
Решение подобных задач обычно связано с оценкой эффективности экспериментального воздействия и оценки его эффекта.
3. Выявление степени согласованности признаков — когда определяют, как количественное или качественное изменение одного признака исследуемой группы влияет на другой признак. Исследователя интересует характер взаимосвязи между этими двумя признаками и возможность давать на её основе
прогнозы.
В этом случае исследователь, доказав наличие взаимосвязи, может попытаться обосновать её, найти подходящее объяснение факту её существования, предсказать реакцию одного из изучаемых признаков в ответ на изменение другого признака эксперимента, что будет иметь большое значение для прогнозирования.
15. Понятие статистической гипотезы. Принятие и отвержение гипотез.
Гипотеза - Предсказание конкретного события или явления, сделанное на основании теории.
Сущность проверки статистической гипотезы – установить, согласуются ли экспериментальные результаты и выдвинутая гипотеза; допустимо ли отнести расхождение между ними за счет случайных величин.
На основании гипотезы можно выстраивать план исследования, результаты которого будут или соответствовать (гипотеза подтверждается), или противоречить (гипотеза не подтверждается) сделанному предсказанию.
р-уровень показывает вероятность ошибки при принятии гипотезы!
Значение p-уровня находится в обратной зависимости от надёжности результата (то есть чем выше p-уровень, тем ниже надёжность и ниже уровень доверия к полученным результатам).
