24 Вопрос. Парабола.

ОПРЕДЕЛЕНИЕ

П араболой называется геометрическое место точек на плоскости, каждая из которых равноудалена от данной точки, называемой фокусом, и данной прямой, называемой директрисой (предполагается, что эта прямая не проходит через фокус

Вывод уравнения параболы

Согласно определению параболы:

FM = KM

О пределяя FM и КМ по формуле расстояния между двумя точками, получим:

К аноническое уравнение параболы

у2 = 2рх (3)

Уравнение (3) называется каноническим уравнением параболы.

Д ля определения вида параболы найдем у из канонического уравнения параболы

Д иректрисса параболы имеет уравнение

26 Вопрос. N-мерное линейное векторное пространство

Векторное пространство R, называется n-мерным, если в нем существует n линейно независимых векторов, а любые n+1 векторов уже являются зависимыми.

Число n называется размерностью векторного пространство R и обозначается dim(R).

Совокупность n линейно независимых векторов n-мерного пространства R называется базисом.

Теорема. Каждый вектор Х векторного пространства R можно представить, и притом единственным способом, в виде линейной комбинации векторов базиса.

27 Вопрос. Системы векторов, операции над ними.

N-мерным вектором называется упорядоченная совокупность n действительных чисел, записываемых в виде Х=(х₁,х₂,…х_n) , где х_i – i-я компонента вектора Х.

Два n-мерных вектора равны тогда и только тогда, когда равны их соответствующие компоненты, т.е. Х=У, если x_i=y_i, i=1…n.

Суммой двух векторов одинаковой размерности n называется вектор Z=X+Y, компоненты которого равны сумме соответствующих компонент слагаемых векторов, т.е. z_i=x_i+y_i , i=1…n.

Произведением вектора Х на действительное число λ называется вектор V=λX, компоненты которого равны произведению λ на соответствующие компоненты вектора Х, т.е. v_i=λx_i , i=1…n.

Линейные операции над векторами удовлетворяют следующим свойствам:

Х + У = У + Х;

(Х + У) + Z = X + (Y + Z);

a(bX) = (ab)X;

a(X + Y) = aX + aY;

(a + b)X = aX + bX;

Существует нулевой вектор О=(0,0,…0) такой, что Х + О = Х, для любого Х;

Для любого вектора Х существует противоположный вектор (-Х) такой, что Х + (-Х) = О;

1∙Х = Х для любого Х.

Определение Множество векторов с действительными компонентами, в котором определены операции сложения векторов и умножения вектора на число, удовлетворяющие приведённым выше свойствам, называется векторным пространством.

28 вопрос. Ранг матрицы

В матрице размера m x n вычеркиванием каких-либо строк и столбцов можно выделить квадратные подматрицы k-го порядка, где k≤min(m; n). Определители таких подматриц называются минорами k-го порядка матрицы А.

Рангом матрицы А называется наивысший порядок отличных от нуля миноров этой матрицы.

Ранг матрицы А обозначается rang A или r(A).

Из определения следует:

1) ранг матрицы размера m x n не превосходит меньшего из её размеров, т.е. r(A) ≤ min (m; n).

2) r(A)=0 тогда и только тогда, когда все элементы матрицы равны нулю, т.е. А=0.

3) Для квадратной матрицы n-го порядка r(A) = n тогда и только тогда, когда матрица А – невырожденная.

В общем случае определение ранга матрицы перебором всех миноров достаточно трудоемко. Для облегчения этой задачи используются элементарные преобразования, сохраняющие ранг матрицы:

1) Отбрасывание нулевой строки (столбца).

2) Умножение всех элементов строки (столбца) матрицы на число, не равное нулю.

3) Изменение порядка строк (столбцов) матрицы.

4) Прибавление к каждому элементу одной строки (столбца) соответствующих элементов другой строки (столбца), умноженных на любое число.

5) Транспонирование матрицы.

Теорема. Ранг матрицы не изменится при элементарных преобразованиях матрицы.

2 9 вопрос. Линейные операторы и матрицы

О пределение. Если задан закон (правило), по которому каждому вектору x пространства ставится в соответствие единственный вектор y пространства то говорят: что задан оператор (преобразование, отображение) A(x), действующий из в и

записывают y=A(x).

Оператор называется линейным, если для любого вектора x и y пространства

и любого числа λ выполняются следующие соотношения:

М атрица называется матрицей оператора в базисе , а ранг r матрицы - рангом оператора .

Т аким образом, каждому линейному оператору соответствует матрица в данном базисе. Справедливо и обратное: Всякой матрице n-го порядка соответствует оператор n-мерного пространства.

С вязь между вектором х и его образом можно выразить в матричной форме:

где - матрица линейного оператора,

О пределим действия над линейными операторами:

• 1 . Суммой двух линейных операторов и называется оператор определяемый равенством

• 2 . Произведением линейного оператора на число λ называется оператор определяемый .

• П роизведением линейных операторов и называется оператор определяемый

• О пределим нулевой оператор переводящий все векторы пространства в нулевые вектора

• и тождественный оператор действующий по правилу

• Теорема Матрицы А и А* линейного оператора в базисах е₁,е₂, ..е_n и е₁^*,е₂^*, ..е_n^* связаны соотношением А*=С^-1АС,

где С – матрица перехода от старого базиса к новому.

33 вопрос. Решение системы линейных уравнений методом Гаусса

М етод Гаусса – метод последовательного исключения переменных – заключается в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого или треугольного вида.

Рассмотрим матрицу:

эта матрица называется расширенной матрицей системы (1), так как в нее кроме матрицы системы А, дополнительно включен столбец свободных членов.

П р и м е р 2. Методом Гаусса решить систему:

Р е ш е н и е. Прямой ход метода Гаусса.

Запишем расширенную матрицу системы,

и с помощью элементарных преобразований

приведём матрицу к треугольному виду:

1. Поменяем местами 1-ю и 2-ю строки.

2. 1-ю строку умножим на (-3) и прибавим ко 2-й,

потом 1-ю умножим на (-2) и прибавим к 3-й.

3. 3-ю строку умножим на (-4) и прибавим ко 2-й,

получим эквивалентную матрицу.

4 . 3-ю строку разделим на 13.

Обратный ход метода Гаусса

34 вопрос. Задачи линейного программирования

Общая задача линейного программирования имеет вид:

Линейная функция называется целевой функцией задачи. Все остальное, за исключением условий неотрицательности переменных x_j, - ограничения.

35 вопрос. Теория двойственности

Двойственная задача- это вспомогательная задача ЛП, получаемая с помощью определенных правил непосредственно из условий исходной задачи

1. Если целевая функция f исходной задачи максимизируется, то целевая функция z двойственной задачи – минимизируется и наоборот.

2. Количество ограничений (m) исходной задачи равно количеству переменных двойственной задачи, а количество переменных (n) исходной задачи равно количеству ограничений двойственной.

Переменные двойственной задачи обозначим y_i (i=1,2, m).

3. Поскольку переменные исходной задачи связаны с ограничениями двойственной, то каждой переменной x_j 0 соответствует в двойственной задаче ограничения вида « » (f→max) или « » (f→min) и наоборот.

4. Каждой переменной x_j неограниченной по знаку, соответствует ограничение вида «=» двойственной задачи, и наоборот.

5. Свободные члены ограничений исходной задачи b_i (i=1,2..m) в двойственной задаче являются коэффициентами при переменных y_i (i=1,2, m) в целевой функции z . Коэффициенты c_j (j=1,2 n) при переменных x_j (j=1,2 n) в целевой функции исходной задачи являются свободными членами ограничений двойственной.

6. Матрица А коэффициентов при неизвестных в ограничениях исходной задачи в двойственной задаче транспонируется А^Т.

36 вопрос. Графическое решение задачи линейного программирования

Исходная задача

1. Максимизация функции f

2.Количеcтво ограничений m

3.Переменные xj (j=1,2 n) i-ое ограничение вида « » хj не ограничено по знаку i-ое ограничение вида «=»

4. Свободные члены ограничений bi Коэффициенты при xj в целевой функции cj

5.Матрица коэффициентов при неизвестных в ограничениях (А)

Двойственная задача

1.Минимизация функции z

2. Количество переменных

3. Количеcтво ограничений n j-ое ограничение вида « » j-ое ограничение вида «=» уi не ограничено по знаку

4. Коэффициенты при yi в целевой функции z (bi) Свободные члены ограничений (cj)

5. Транспонированная матрица коэффициентов при неизвестных в ограничениях (АТ).

37 вопрос. Симплексный метод

Для решения задачи симплекс-методом необходимо привести её к каноническому виду и определить исходное допустимое базисное решение. Отталкиваясь от этого решения с помощью алгоритма симплекс-метода приходят к оптимальному решению или выводу о том, что задача не имеет решения.

Алгоритм симплекс-метода

1. Приводим задачу к каноническому виду.

2. Выбираем базисные переменные. У базисных переменных должен быть единичный вектор-столбец.

3 . Полагая небазисные переменные равные нулю, находим значения базисных переменных. Это будет первое базисное решение

и значение целевой функции f.

4.Составляем таблицу.

Если в нулевой строке все коэффициенты при небазисных переменных , то найденное решение оптимально. В противном случае для нахождения нового базисного решения необходимо выбрать переменную вводимую в базис (т.е. выбрать ведущий столбец) и переменную выводимую из базиса (т.е. выбрать ведущую строку).

5. Для выбора ведущего столбца ( переменной вводимой в базис) среди коэффициентов небазисных переменных в 0-ом уравнении (в целевой функции) выбираем наименьший, и эту переменную вводим в базис.

Для выбора переменной выводимой из базиса (выбор ведущей строки) рассматриваем положительные отношения столбца свободных членов к ответствующим элементам ведущего столбца. Строка, отвечающая наименьшему отношению будет ведущей.

6. Из уравнения, отвечающего ведущей строке, находим выражение для переменной вводимой в базис и подставляем его в остальные уравнения.

7. В результате получилась новая система уравнений, и процесс повторяется.

38 вопрос. Транспортная задача

Пусть имеется m поставщиков А₁, А₂, …А_m однородного груза в количества а₁, а₂, а_m единиц и n потребителей В₁, В₂, …В_n этого груза, потребность которых составляет соответственно в₁,в₂, в_n единиц.

Известны стоимости перевозок единицы груза от i-го поставщика к j-му потребителю

с_ij (i=1, 2,…m, j=1,2,…n).

Требуется составить такой план перевозок, который обеспечит минимальные транспортные расходы.

Исходные данные транспортной задачи записываются в виде таблицы

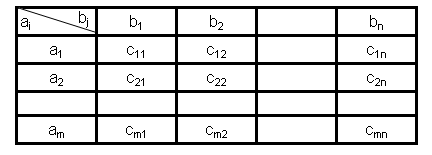
Переменные х_ij (i=1, 2,…m, j=1,2,…n) – объемы перевозок

от каждого от i-го поставщика к j-му потребителю.

Эти переменные могут быть записаны в виде матрицы перевозок.

М атематическая модель транспортной задачи

Целевая функция задачи (А) выражает требование обеспечить минимум суммарных затрат на перевозку всех грузов.

Группа из m уравнений (В) описывает тот факт, что запасы всех m поставщиков вывозятся полностью.

Группа из n уравнений (С) выражает требование полностью удовлетворить запросы всех n потребителей.

Неравенство (D) является условиями неотрицательности всех переменных задачи.

Таким образом математическая формулировка транспортной задачи состоит в следующем:

Найти матрицу Х =( х_ij ) i=1, 2,…m, j=1,2,…n, элементы которой удовлетворяют системе ограничений (В) и (С), условиям неотрицательности (D) и обеспечивают минимум целевой функции (А).

В рассматриваемой модели транспортной задачи предполагается, что суммарные запасы поставщиков равны суммарным запросам потребителей т.е

Такая задача называется задачей с правильным балансом, а её модель закрытой. Если это равенство не выполняется, то модель называется задачей с неправильным балансом, а её модель – открытой.