20 Вопрос. Операции над матрицами.

Умножение матрицы на число.

Произведением матрицы А на число λ называется матрица В=λА, элементы которой b_ij =λ а_ij для всех i=1… m; j=1… n.

Сложение матриц.

Суммой двух матриц А и В одинакового размера mxn называется матрица С=А+В, элементы которой с_ij =а_ij+ b_ij для всех i=1… m; j=1…n.

Вычитание матриц.

Разность двух матриц одинакового размера определяется через предыдущие операции: А – В = А + ( −1 )∙В.

Умножение матриц.

Умножение матриц А на матрицу В определено, когда число столбцов первой матрицы равно числу строк второй. Тогда произведением матриц называется такая матрица , каждый элемент которой с_ij равен сумме произведений элементов i-й строки матрицы А на соответствующие элементы j-го столбца матрицы В.

Целой положительной степенью А^m квадратной матрицы А называется произведение m матриц А, т.е. Аm = А ∙А∙ …∙А

Транспонирование матрицы.

Транспонированием матрицы называется переход от матрицы А к А^т (или А'), в которой строки и столбцы поменялись местами с сохранением порядка. А^т – называется транспонированной относительно матрицы А.

21 Вопрос. Прямая линия на плоскости.

ОПРЕДЕЛЕНИЕ

Уравнение прямой, заданное уравнением первой степени общего вида Ax+By+C=0, называется уравнением прямой общего вида

Рассмотрим случаи:

В=0 → Ах+С=0 → прямая параллельная оси ОУ.

В≠0 → Ву= -Ах-С → y=kx+b уравнение прямой с угловым коэффициентом, где k=-A/B, b=- C/B.

ОПРЕДЕЛЕНИЕ

Угловым коэффициентом прямой называется тангенс угла, на который нужно повернуть против часовой стрелки ось Ох вокруг начала координат О, чтобы прямая стала параллельна этой оси.

Уравнение прямой с угловым коэффициентом.

Уравнение (1) называется уравнением прямой с угловым коэффициентом

22 Вопрос. Эллипс.

ОПРЕДЕЛЕНИЕ

Эллипсом называется геометрическое место точек на плоскости, для которых сумма расстояний от двух фиксированных точек плоскости, называемых фокусами, есть постоянная величина равная 2а.

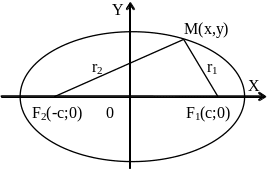
Эллипс

Обозначим F1F2=2c. Тогда координаты фокуса F1 будут (с;0), а координаты фокуса F2 будут (-с;0).

Определим r1 и r2 по формулам расстояния между двумя точками

На основании определения эллипса как геометрического места точек должно выполняться равенство:

r1+r2=2a

вывод канонического уравнения эллипса

Преобразовав получим: каноническое уравнение эллипса

В уравнении эллипса содержатся только члены с четными степенями текущих координат. Отсюда следует важная геометрическая особенность: эллипс, определяемый уравнением (2) симметричен как относительно оси Ox, так и относительно оси Oy .

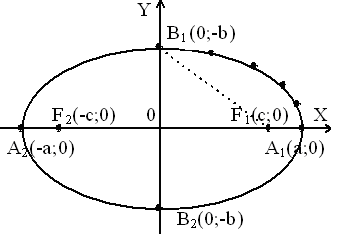эллипс

23Вопрос. Гипербола.

ОПРЕДЕЛЕНИЕ

Г иперболой называется геометрическое место точек на плоскости, для которых разность расстояний от двух фиксированных точек плоскости, называемых фокусами, есть величина постоянная равная

Ф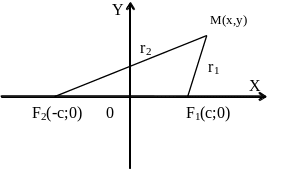 окусы гиперболы обозначим через F1 и F2, а расстояние между ними - через 2с

На основании определения гиперболы как геометрического места точек на плоскости, можно утверждать, что для всех точек гиперболы и только для них, должно выполняться равенство

r1 - r2 = ± 2a

П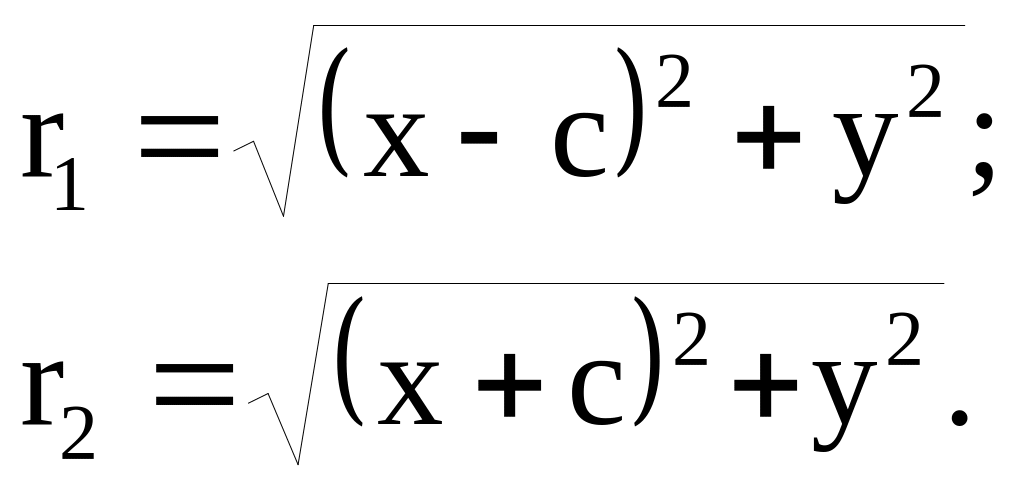 о формуле расстояния между двумя точками имеем:

Г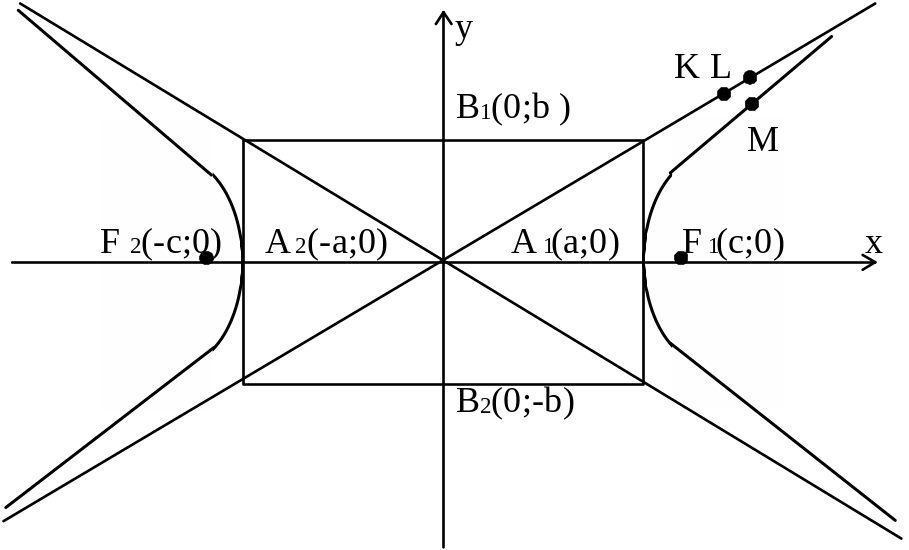 ипербола

А симптотами гиперболы называются прямые, имеющие уравнения