9. Понятие тела давления. Закон Архимеда.

Тело давления – тело ограниченное поверхностью, на кот действует гидростатическое давление, свободной поверхностью или ее продолжением и вертикальными плоскостями, проходящей через верх и нижние точки поверхности

Рассмотрим теперь погруженное в жидкость тело произвольной формы (рис. 2.12).

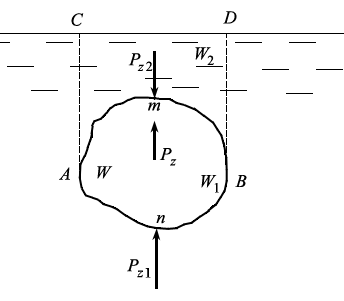Рис. 2.12

Определим силы давления на него в проекциях на оси координат.

Горизонтальные составляющие силы давления на тело P_x будут одинаковы с обеих сторон тела, поскольку проекция его боковой криволинейной поверхности на вертикальную плоскость ω_yz, взятая справа и слева, будет одна и та же. Аналогично этому, будут одинаковы и горизонтальные составляющие P_y в направлении оси y (проекции поверхности на ось ω_xz). Значит, горизонтальные составляющие сил гидростатического давления взаимно уравновешиваются и не влияют на состояние погруженного тела.

Вертикальные же составляющие будут различны. Действительно, сила давления на нижнюю часть тела – P_z1 – действует на поверхность AnB, направлена вертикально вверх и равна

,

где W₁ – объем, ограниченный поверхностью ACDBn.

Сила давления на верхнюю часть тела P_z2, т. е. на поверхность AmB, направлена вниз и равна

,

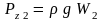где W₂ – объем, ограниченный поверхностью ACDBm.

Результирующая вертикальная составляющая силы давления будет равна их разности:

,

(2.17)

где W – объем тела.

Полученная формула (2.17) выражает закон Архимеда: на тело, погруженное в жидкость, действует направленная вверх выталкивающая сила, равная весу жидкости, вытесненной этим телом.

Из закона Архимеда следует условие плавания тел:

• если вес тела больше выталкивающей силы 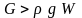, то тело тонет;

• при 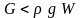тело всплывает;

• когда тело находится во взвешенном состоянии.

Здесь следует сделать оговорку: поскольку сила давления действует по нормали к поверхности жидкости, то в случае, если тело (например, судно) плавает на поверхности потока жидкости, имеющего уклон 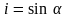, подъемная сила (сила давления) будет направлена не вертикально, а по нормали к свободной поверхности и будет равна весу вытесненного объема жидкости, умноженному на .

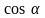Еще одно интересное приложение – давление на дно тела, лежащего на дне и плотно соприкасающегося частью своей поверхности с дном (рис.2.13).

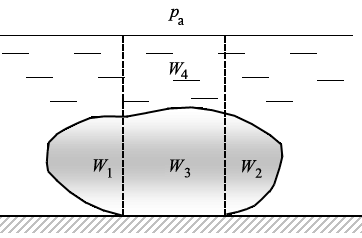
Рис. 2.13

Здесь учтем также наличие над поверхностью жидкости атмосферного давления p_aтм. Тогда для случая, изображенного на рис. 2.13, давление тела на дно водоема будет:

.

(2.18)

Здесь: ρ_т – плотность материала тела, ρ_в – плотность воды;

W₁ и W₂ – объемы частей тела, нависающих над дном;

W₃ – объем средней части тела, опирающейся на дно;

W₄ – объем столба воды над опирающейся частью тела;

ω – площадь соприкасания тела с дном.

Поправочный коэффициент K < 1 вводится потому, что соприкаса-ние обычно не является полным.

Полученное соотношение (2.18) будет приближенным, так как в действительности между телом и дном образуется пленка жидкости, и в ней могут возникнуть силы гидростатического давления на тело.
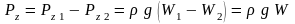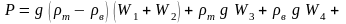
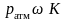