5. Примеры эпюр гидростатического давления

Эпюра абсолютного гидростатического давления представляет собой трапецию, а эпюра избыточного — треугольник (рис. а).

Если плоская стенка, на которую действует жидкость, наклонена к горизонту под углом a (рис.   б), то основное уравнение гидростатики принимает следующий вид:

Таким образом, эпюры абсолютного и избыточного гидростатического давления на наклонную стенку представляют собой соответственно наклонную трапецию и наклонный треугольник.

Если плоская стенка, на которую с двух сторон оказывает воздействие жидкость, вертикальна, то на нее будут действовать параллельные и противоположно направленные силы гидростатического давления. Эпюра гидростатического давления на вертикальную стенку представляет собой вертикальную трапецию.

Эпюра гидростатического давления на горизонтальное дно резервуара представляет собой прямоугольник, так как при постоянной глубине избыточное давление на дно постоянно.

6. Поверхности равного давления. Примеры

Поверхностью уровня или поверхностью равного давления называется такая поверхность в жидкости, давление во всех точках которой одно и то же, т. е. на такой поверхности dp = 0.

Так как давление является некоторой функцией координат, т. е. p = f(x,y,z), то уравнение поверхности равного давления будет:

p = f(x, y, z) = C = const.

(2.9)

Придавая константе C разные значения, будем получать различные поверхности уровня. Уравнение (2.9) есть уравнение семейства поверхностей уровня.

Свободная поверхность – это поверхность раздела капельной жидкости с газом, в частности, с воздухом. Обычно про свободную поверхность говорят только для несжимаемых (капельных) жидкостей. Понятно, что свободная поверхность является и поверхностью равного давления, величина которого равна давлению в газе (на поверхности раздела).

По аналогии с поверхностью уровня вводят понятие поверхности равного потенциала или эквипотенциальной поверхности – это поверхность, во всех точках которой силовая функция имеет одно и то же значение. Т. е. на такой поверхности

U = const или .

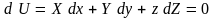Тогда уравнение семейства эквипотенциальных поверхностей будет иметь вид U(x,y,z) = C,

где постоянная C принимает различные значения для разных поверхностей.

Из интегральной формы уравнений Эйлера (уравнения (2.3)) следует, что

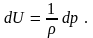
Из этого соотношения можно сделать вывод, что поверхности равного давления и поверхности равного потенциала совпадают, потому что при dp = 0 и dU = 0.

Важнейшее свойство поверхностей равного давления и равного потенциала состоит в следующем: объемная сила, действующая на частицу жидкости, находящуюся в любой точке, направлена по нормали к поверхности уровня, проходящей через эту точку.

Докажем это свойство.

Пусть частица жидкости из точки с коорди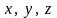натами переместилась по эквипотенциальной поверхности в точку с координатами 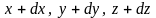. Работа объемных сил на этом перемещении будет равна

.

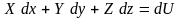Но, поскольку частица жидкости перемещалась по эквипотенциальной поверхности, dU = 0. Значит работа объемных сил, действующих на частицу, равна нулю. Силы не равны нулю, перемещение не равно нулю, тогда работа может быть равна нулю только при условии, что силы перпендикулярны перемещению. То есть объемные силы нормальны к поверхности уровня.

Обратим внимание на то, что в основном уравнении гидростатики, записанном для случая, когда на жидкость действует только один вид объемных сил – силы тяжести (см. уравнение (2.5)) ,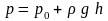

величина p₀ – не обязательно давление на поверхности жидкости. Это может быть давление в любой точке, в которой оно нам известно. Тогда h – это разность глубин (по направлению вертикально вниз) между точкой, в которой давление известно, и точкой, в которой мы хотим его определить. Таким образом, с помощью этого уравнения можно определить значение давления p в любой точке через известное давление в известной точке – p₀.

Заметим, что величина 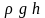не зависит от p₀. Тогда из уравнения (2.5) следует вывод: насколько изменится давление p₀, настолько же изменится и давление в любой точке объема жидкости p. Поскольку точки, в которых фиксируем p и p₀, выбраны произвольно, это означает, что давление, создаваемое в любой точке покоящейся жидкости, передается ко всем точкам занимаемого объема жидкости без изменения величины.

Как известно, в этом и состоит закон Паскаля.

По уравнению (2.5) можно определить форму поверхностей уровня покоящейся жидкости. Для этого надо положить p = const. Из уравнения следует, что это выполнимо лишь при h = const. Значит, что при действии на жидкость из объемных сил только сил тяжести, поверхности уровня представляют собой горизонтальные плоскости.

Такой же горизонтальной плоскостью будет и свободная поверхность покоящейся жидкости.