5.4.3. Внезапное сужение русла (трубы)

Внезапное сужение вызывает меньшую потерю энергии, чем внезапное расширение с таким же соотношением площадей. Потери при этом обусловлены:

• трением потока при входе в более узкую трубу;

• потерями на вихреобразование.

Вихри образуются потому, что поток не обтекает входной угол, а срывается с него и сужается. Кольцевое пространство вокруг суженной части заполняется завихренной жидкостью (рис. 5.9).

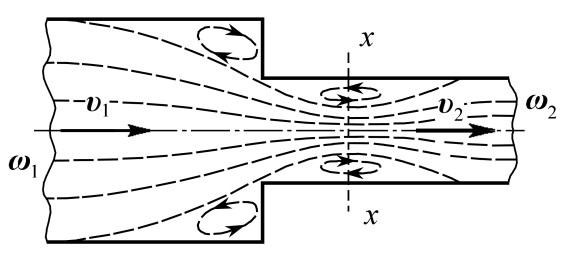
Рис. 5.9

Далее поток расширяется и при расширении происходит потеря напора, определяемая формулой Борда (5.6).

.

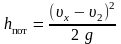Тогда полная потеря напора будет

,

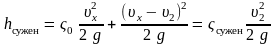здесь ζ ₀ – коэффициент потерь, обусловленный трением потока при входе в узкую трубу и зависящий от соотношения площадей и Re;

_x – скорость потока в суженном месте;

ζ_сужен – коэффициент сопротивления внезапного сужения.

Для практических расчетов удобно пользоваться полуэмпирической формулой И. Е. Идельчика

.

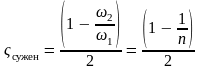Здесь 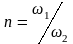– степень сужения.

Из формулы И. Е. Идельчика следует, что в частном случае при 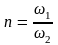= 0, т. е. при выходе из очень большого резервуара в трубу (при отсутствии закругления) коэффициент сопротивления ζ_сужен = ζ_вх = 0,5.

Значительно уменьшить потерю напора при входе в трубу можно закруглением входного угла (входной кромки).

5.4.4. Постепенное сужение трубы

Коническая сходящаяся труба называется конфузором (рис. 5.10).

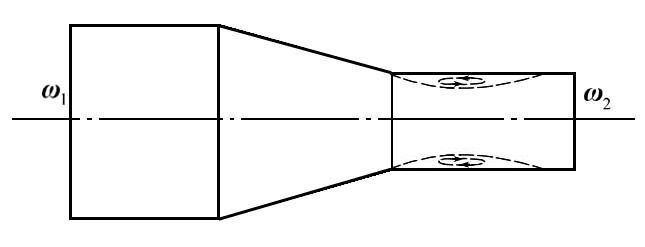
Рис. 5.10

В конфузоре течение жидкости происходит при увеличении скорости и падении давления вниз по потоку. Поэтому причин для вихреобразования и срыва потока (как в диффузоре) нет. В конфузоре есть лишь потери на трение, следовательно сопротивление его всегда меньше, чем у такого же диффузора.

Потерю напора в конфузоре можно подсчитать так же, как мы это делали для диффузора: выразить потерю напора для элементарного отрезка и проинтегрировать по всему объему. Тогда в результате получим

.

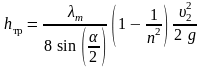Небольшие вихреобразования и отрыв потока от стенки с одновременным сжатием потока могут возникнуть лишь на выходе из конфузора в месте соединения конической части с цилиндрической. Чтобы этого не происходило, рекомендуется коническую часть плавно сопрягать с цилиндрической или коническую часть заменить криволинейной, плавно переходящей в цилиндр. Такое решение допускает значительную степень сужения при малой длине вдоль оси, потери при этом небольшие. Такое плавное сужение называется соплом. Коэффициент сопротивления сопла находится примерно в пределах ζ = 0,03÷0,1 в зависимости от степени и плавности сужения и числа Re (чем больше Re, тем меньше ζ).

5.4.5. Внезапный поворот русла

Внезапный поворот трубы или русла в гидравлике называют также коленом (рис. 5.11).

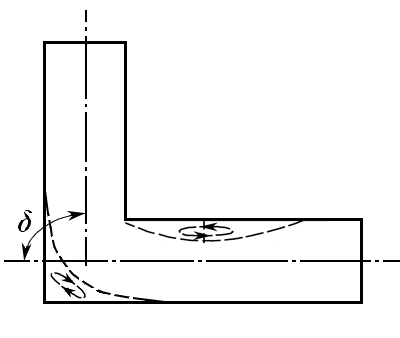
Рис. 5.11

Колено обычно вызывает значительные потери энергии, так как происходят отрыв потока и вихреобразование, причем эти потери тем больше, чем больше угол δ – угол поворота колена.

Потерю напора рассчитывают по общей формуле

.

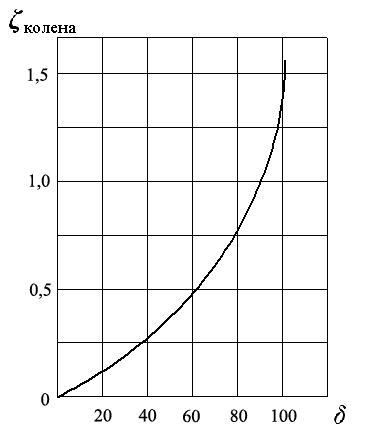
Рис. 5.12

Коэффициент сопротивления колена круглого сечения возрастает с увеличением δ очень круто и при δ = 90º достигает единицы (рис. 5.12).