5.4.2. Постепенное расширение русла

Постепенно расширяющаяся труба называется диффузором (рис. 5.6).

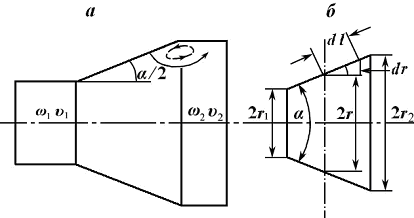
Рис. 5.6

При течении в диффузоре скорость уменьшается, давление вниз по потоку соответственно увеличивается, происходит преобразование кинетической энергии в энергию давления. Частицы двигающейся жидкости преодолевают нарастающее давление за счет кинетической энергии. Кинетическая энергия убывает вдоль оси диффузора и, что важно, от оси к стенкам. Слои жидкости вдоль стенки обладают такой малой кинетической энергией, что порой не в состоянии преодолеть встречное повышенное давление – они останавливаются или даже начинают двигаться обратно. Это вызывает противоток, вихреобразование и даже отрыв потока. Интенсивность этих процессов возрастает с увеличением угла расширения диффузора (угла α), следовательно, при увеличении угла расширения диффузора растут и потери на вихреобразование.

Кроме того, в диффузоре имеются обычные потери на трение, подобные тем, что возникают в трубах постоянного сечения.

Поэтому полную потерю напора в диффузоре представим как сумму двух слагаемых:

.

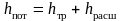Определим слагаемые в этой формуле.

Потерю напора на трение рассчитаем следующим образом. Рассмотрим круглый диффузор с прямолинейной образующей и углом 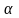при вершине (рис. 5.6.б). Радиус входного отверстия – r₁, выходного – r₂. По длине диффузора радиус изменяется, соответственно меняется и скорость течения жидкости. Возьмем элементарный отрезок диффузора длиной по образующей dl, запишем для него выражение для потери напора.

По формуле Вейсбаха–Дарси для всего участка трубы

.

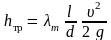Тогда для элементарного отрезка

.

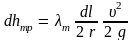Здесь r – текущий радиус сечения, – средняя скорость в этом сечении.

Из геометрии (рис. 5.6.б) следует, что

.

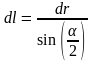Так как расход при течении вдоль диффузора сохраняется, то

,

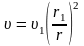где r₁ и 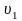– соответственно радиус трубы и скорость в начале диффузора.

Подставим определенные таким образом значения dl и в выражение для dh_тр и проинтегрируем в пределах от r₁ до r₂, т. е. по всей длине диффузора. Считаем коэффициент λ_т постоянным.

,

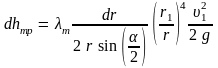откуда

.

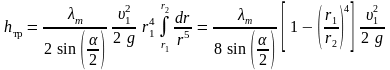Введем понятие степени расширения диффузора

.

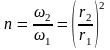Тогда:

.

(5.9)

Потери напора на расширение (на вихреобразование) имеют в диффузоре ту же природу, что и в трубопроводе с внезапным расширением сечения, но, по сравнению с внезапным расширением, они меньше. Обычно вводят поправочный коэффициент k, меньший единицы, и, используя формулы (5.6) и (5.8), получают

.

(5.10)

Так как в диффузоре по сравнению с внезапным расширением торможение как бы смягченное, коэффициент k называют коэффициентом смягчения.

Для углов конусности диффузора 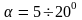значение коэффициента k принимают приближенно:

.

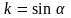Тогда, используя формулы (5.9) и (5.10), можно записать

.

Коэффициент сопротивления диффузора можно выразить формулой:

.

(5.11)

Видим, что коэффициент сопротивления диффузора зависит от угла , коэффициента λ_т и степени расширения n.

Выясним, как ζ_диф зависит от угла при постоянных λ_т и степени расширения n (постоянство n означает постоянство отношения r₁ и r₂).

В формуле (5.11) первое слагаемое обусловлено трением, второе – расширением. При увеличении первая составляющая ζ_диф уменьшается, так как диффузор становится короче, а вторая составляющая увеличивается. При уменьшении вихреобразование (вторая составляющая) уменьшается, но возрастает трение, так как диффузор удлиняется.

Функция ζ_диф = f( ) имеет минимум при некотором наивыгодней-шем оптимальном значении угла (рис. 5.7). Это значение можно найти, продифференцировав по зависимость коэффициента сопротивления от угла раствора диффузора, приравняв производную нулю и решив полученное уравнение относительно .

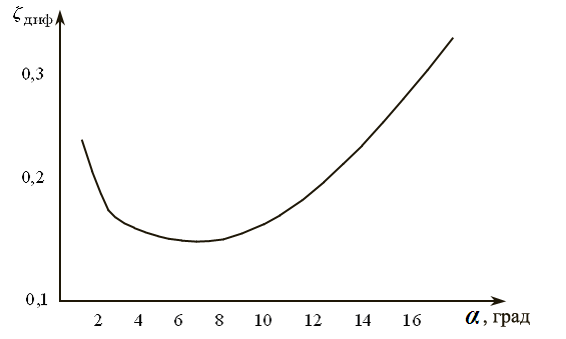
Рис. 5.7

Расчеты дают следующее оптимальное значение угла :

.

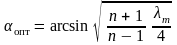При использовании типовых (обычных) значений λ_т = 0,015÷0,025 и n = 2÷4, расчет дает значение _опт = 6º. Для сокращения длины диффузора можно принимать несколько большие углы – от 7º до 9º.

Такие же значения оптимального угла можно рекомендовать и для квадратных диффузоров.

Для плоских диффузоров (прямоугольных с расширением в одной плоскости) оптимальный угол больше и составляет 10–12º.

Иногда габариты конструкций не позволяют использовать диффузоры c оптимальными углами. Тогда возможно применение диффузора с криволинейной образующей (рис. 5.8.а). Такой диффузор обеспечивает постоянный градиент давления вдоль оси (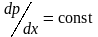 ), т. е. равномерное нарастание давления (при прямой образующей градиент давления убывает вдоль диффузора). Уменьшение потери энергии в таких диффузорах тем больше, чем больше угол . Кроме того, поток в таких диффузорах отличается устойчивостью, т. е. меньше тенденций к отрыву потока.

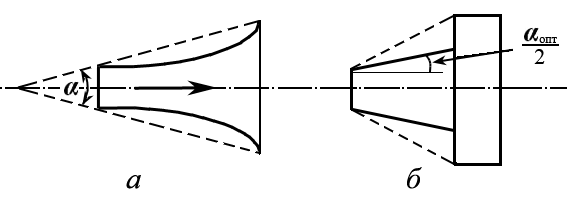
Рис. 5.8

Возможно применение также ступенчатого диффузора – обычного диффузора с прямолинейной образующей и оптимальным углом, и следующего за ним внезапного расширения (рис. 5.8.б). Диффузор с оптимальным углом существенно снижает скорости течения, и поэтому последующее внезапное расширение не вызывает больших потерь энергии. Общее сопротивление такой составной конструкции значительно меньше, чем у обычного диффузора такой же длины и с той же степенью раскрытия.
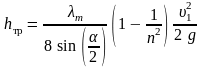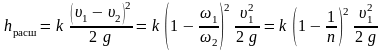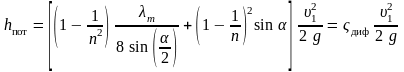