5.3. Графики и. И. Никурадзе

Исследования, проведенные И. И. Никурадзе в 1932 – 1933 годах показали, что в общем случае коэффициент λ зависит от числа Re и от так называемой относительной шероховатости.

«Относительная шероховатость» – отношение некоторой средней (как правило, условной) высоты выступов шероховатости к диаметру трубы, т. е. .

Технические трубы – это трубы с естественной шероховатостью, обусловленной материалом стенок, технологией изготовления, условиями и продолжительностью эксплуатации. Понятно, что абсолютные значения величин выступов шероховатости не могут являться полной характерис-тикой шероховатости поверхностей – у различных поверхностей выступы имеют различную конфигурацию и разное распределение по поверхности. Поэтому вводится понятие эквивалентной шероховатости. Эквивалентная шероховатость – это высота выступа воображаемой равнозернистой шероховатости, при которой потери напора и значения коэффициента Дарси такие же, как и для реальной шероховатости.

В своих опытах И. И. Никурадзе использовал латунные трубы различного диаметра (от 10 до 100 мм). Для создания разной шероховатости на внутреннюю поверхность труб лаком приклеивался слой песчинок примерно одинакового диаметра – Δ. В опытах значения относительной шероховатости изменялись от до . Числа Рейнольдса в опытах Никурадзе изменялись в диапазоне Re = 500 ÷ 10 ⁶.

По результатам опытов Никурадзе были построены графики зависимости коэффициента λ от числа Re и от относительной шероховатости в логарифмических координатах – рис. 5.4.

На графиках можно выделить следующие характерные зоны:

1. Зона ламинарного течения, где , потери зависят от скорости в первой степени, и шероховатость не влияет на величину λ. Линии на графике в этой зоне практически совпадают.

2. Зона переходная от ламинарного к турбулентному течению, Re = 2000 ÷ 3000. В этой зоне тоже λ = f(Re), но конкретный вид этой зависимости не достаточно определен. Критическое число Рейнольдса перехода от ламинарного к турбулентному течению от шероховатости практически не зависит, графики отклоняются от прямой приблизительно при одном и том же числе Re_кр.

В этой зоне применимы, например, такие эмпирические зависимости для определения коэффициента потерь:

или .

3. Зона, соответствующая началу турбулентного течения, но при еще небольших значениях Re. Шероховатость на величину λ практически не влияет, поэтому эта зона называется зоной «гидравлически гладких труб». В этой зоне также λ = f(Re), а потери напора пропорциональны скорости в степени 1,75: . Коэффициент λ в этой зоне можно определить из формул

или (для Re ≤ 10⁵).

При увеличении Re и в этой зоне начинает сказываться шероховатость – кривые для более шероховатых труб начинают отклоняться от прямой, соответствующей закону сопротивления гладких труб.

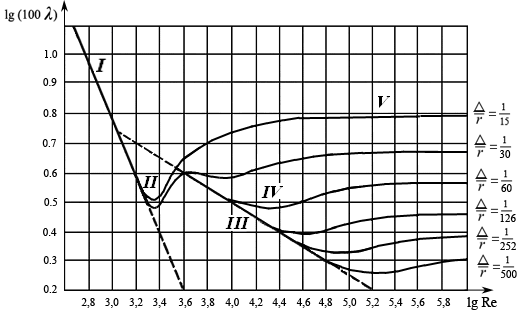
Рис. 5.4

4. Зона турбулентного течения, переходная от «гидравлически гладких труб» к зоне «шероховатых» труб. В этой зоне λ зависит и от Re, и от относительной шероховатости. Здесь коэффициент λ можно определить из формулы

.

Потери напора в этой зоне пропорциональны скорости в степени между 1,75 и 2,0.

5. Зона развитого турбулентного течения – зона «шероховатых труб» или зона «квадратичного сопротивления». Здесь λ не зависит от Re, а зависит только от относительной шероховатости . Потери напора пропорциональны квадрату скорости .

Коэффициент λ в этой зоне можно определять по зависимостям:

или .

Во всех трех зонах с турбулентным течением для определения коэффициента потерь на трение можно использовать формулу

.

Таким образом, для всех трех турбулентных зон влияние шероховатости оценивается следующим образом.

Турбулентный поток можно представить состоящим из основной турбулентной зоны и пристенного (пограничного) слоя. При турбулентном течении с небольшим значением числа Re толщина ламинарного пограничного слоя превышает высоту шероховатостей. Шероховатость, как бы прикрытая этим слоем, не оказывает влияния на сопротивление.

С увеличением Re толщина пограничного слоя уменьшается и становится меньше размера Δ. Шероховатость частично выступает из пограничного слоя и начинает влиять на сопротивление потока.

При больших числах Re пограничный слой становится очень тонким, шероховатости почти полностью выступают из него, бугорки обтекаются турбулентным потоком с вихреобразованиями за каждым бугорком, этим и объясняется квадратичный закон сопротивления.

В справочниках, составленных для определения значений коэффициента потерь λ, приведены значения «эквивалентной шероховатости» для различных материалов труб – стали, чугуна, бетона и проч. Кроме того, в справочниках даются и значения коэффициентов местного сопротивления ζ для конкретных конструкций местных сопротивлений.