19. Формулы для скорости, расхода и потерь напора в круглой цилиндрической трубе при ламинарном режиме.

Определим распределение скорости и расход жидкости при ламинарном движении ее в круглой цилиндрической трубе.

При течении жидкости в трубе различают начальный, или входной, участок и участок установившегося течения. Если вход в трубу из резервуара выполнен достаточно плавным, то в начальном сечении распределение скоростей практически равномерное, эпюра скорости представляет собой прямоугольник (рис. 4.2). По мере продвижения жидкости по начальному участку на стенках за счет сил трения возникает торможение. При дальнейшем движении жидкости по трубе тормозящее действие стенок распространяется на все большую толщу потока.

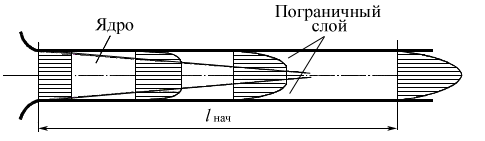
Рис. 4.2

На начальном участке поток имеет все уменьшающееся ядро, в котором сохраняется равномерное распределение скоростей, и пристеночный пограничный слой, где скорости распределены неравномерно. Вниз по течению размеры ядра убывают, толщина пограничного слоя растет до почти полного смыкания на оси трубы. Дальше начинается участок установившегося движения, который мы, собственно, и рассмотрим.

В соответствии с формулой Ньютона, сила гидравлического трения в жидкости равна

.

Запишем ее в цилиндрической системе координат в виде

,

где r – текущий радиус цилиндрического слоя.

Отнеся силу к единице площади, получим напряжение .

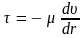С другой стороны, в соответствии с основным уравнением равномерного движения жидкости (формула (3.12)), имеем для напряжения трения

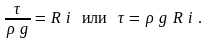
Тогда

Вспоминая, что гидравлический радиус для круглой трубы , и разделяя переменные, получим

Интегрируем:

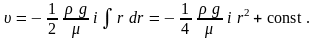
Постоянную интегрирования определяем из граничных условий: при r = r₀ (т. е. на стенке трубы) должны выполняться условия прилипания и скорость жидкости должна быть равна нулю, = 0. Тогда

Подставляя значение постоянной интегрирования в формулу для определения скорости, получаем

(4.2)

Отсюда видно, что скорости в поперечном сечении трубы распределяются по параболическому закону. Наибольшая скорость будет при r = 0, т. е. в центре трубы:

(4.3)

Можно ли упростить формулу (4.2)?

При ламинарном движении скорости малы, скоростные напоры (слагаемые в уравнении Бернулли, характеризующие кинетическую энергию жидкости) тоже малы, поэтому можно считать, что полная удельная энергия жидкости определится только двумя членами уравнения Бернулли: .

Тогда вместо полного гидравлического уклона можно ввести величину , понимая под h запас энергии в первом сечении относительно второго, равный . Этот запас часто называют действующим напором.

Тогда формула для скорости запишется в виде

(4.4)

Выведем теперь формулу для расхода.

Выделим в сечении потока элементарное кольцо, образованное двумя концентрическими окружностями, радиусы которых отличаются на малую величину dr (рис. 4.3). Расход жидкости через сечение этого кольца

Подставим в эту формулу выражение для скорости (4.4)

Для определения полного расхода через сечение трубы проинтегрируем это выражение по r в пределах от 0 до r₀:

(4.5)

r₀

r dr

Рис. 4.3

Среднюю скорость вычислим по формуле :

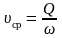(4.6)

Сравнивая с _max из (4.3), видим, что _ср = 0,5 _max.

При переходе ламинарного течения в турбулентное характер распределения скоростей по сечению трубы изменяется. Если при ламинарном течении распределение скорости по сечению имеет параболический характер, то при турбулентном течении эпюра скоростей из-за перемешивания потока выравнивается, приближаясь к прямоугольной. Так как при турбулентных течениях скорость в каждой точке потока непрерывно пульсирует по величине и направлению (в определенных пределах), то для построения эпюр скоростей и при технических расчетах используются осредненные по времени значения скоростей.

Заметим еще, что при переходе от ламинарного к турбулентному течению не весь поток полностью турбулизируется: около стенок остается тонкий – так называемый пограничный – слой, в котором течение остается ламинарным.

Таким образом, получается, что при турбулентном движении _ср = (0,8 ÷ 0,9) _max.

Определим связь средней скорости движения жидкости при ламинарном и турбулентном режимах течения в трубопроводе с потерей напора.

Учитывая, что , для ламинарного режима из формулы (4.6) получим

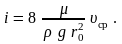
Из этой формулы видно, что потери напора при ламинарном течении пропорциональны первой степени скорости.

При турбулентном же течении потери напора пропорциональны скорости в степени m, меняющейся от 1,75 до 2,00. Таким образом, общий характер зависимости потерь напора от скорости можно выразить так:

• при ламинарном режиме

• при турбулентном режиме

где k₁ и k₂ – соответствующие коэффициенты пропорциональности.

Отметим, что общий случай движения вязкой жидкости описывается дифференциальными уравнениями Навье–Стокса

Оператор Лапласа 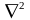предполагает следующую операцию над своим переменным аргументом

.

Уравнения Навье–Стокса отличаются от уравнений Эйлера для идеальной жидкости наличием членов с вязкостью . В уравнениях Навье–Стокса четыре неизвестных – три проекции скорости и давление. Привлекая уравнение неразрывности в дифференциальной форме, получаем замкнутую систему для нахождения неизвестных. Но общего решения эти уравнения не имеют, их можно решить лишь для некоторых частных случаев. Например, формула (4.2) и есть частное решение для установившегося ламинарного течения вязкой жидкости в круглой цилиндрической трубе.

20. Элементы теории турбулентности. Мгновенные и осредненные скорости. Формула Лоренца для касательных напряжений при турбулентном движении. Логарифмический закон распределения скоростей по сечению,

Турбулентное движение характеризуется непрерывным перемешиванием частиц жидкости. Частицы, движущиеся преимущественно в продольном направлении по потоку, имеют и поперечные перемещения, траектории их движения чрезвычайно сложны.

Турбулентное движение по существу является неустановившимся, так как скорости в любой точке потока непрерывно и постоянно изменяются во времени, т. е. пульсируют по величине и направлению относительно среднего значения (рис. 4.4).

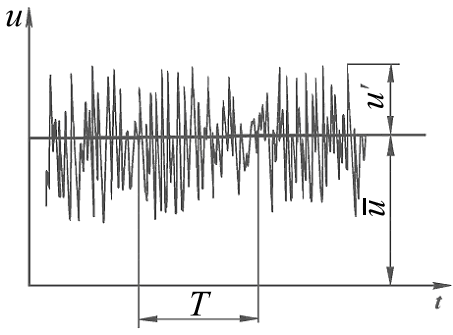
Рис. 4.4

Такие пульсации скорости и являются самым характерным свойством турбулентного течения. У стенок, ограничивающих поток, пульсации затухают, так как поперечные перемещения частиц затруднены. Частицы движутся по извилистым траекториям почти параллельно стенкам, либо течение переходит в ламинарный режим.

Скорость жидкой частицы в данной точке в данный момент времени называют мгновенной. При изучении турбулентного потока пользуются понятием осредненной скорости. Осредненная скорость – это средняя скорость в данной точке, взятая за период времени, существенно больший периодов пульсаций, но меньший характерных времен изменения параметров потока: ,

где T – период осреднения; u – мгновенная скорость в точке.

Отклонение мгновенной скорости от ее осредненного значения называется пульсацией скорости – (рис. 4.4).

Как отмечено выше, при вполне развитом турбулентном течении _ср = (0,8 ÷ 0,9) _max. Эпюра скорости при турбулентном течении в трубе приведена на рис. 4.5.

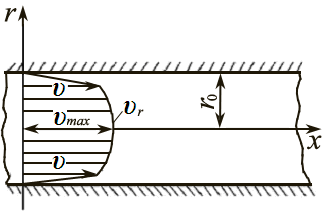
Рис. 4.5

Формула для потери напора при развитом турбулентном режиме течения имеет вид , где m следует принять равным 2. Тогда .

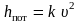Поскольку потери напора при движении жидкости обусловлены внутренним трением, то и характер поведения касательных напряжений в потоке будет таким же, т. е. пропорциональным квадрату скорости: ,

где ψ – коэффициент пропорциональности.

Используя основное уравнение движения жидкости (3.12), можно записать

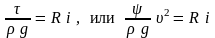,Откуда

Определяем отсюда скорость

Введем новый коэффициент C, обозначив . Тогда окончательно получим:

.

(4.7)

Это – формула Шези для средней скорости равномерного турбулентного течения жидкости. Она была выведена еще в XVIII веке.

Коэффициент C имеет размерность .

Изначально считали, что коэффициент C – величина постоянная или меняющаяся в небольших пределах – примерно 40 – 50. Однако выяснилось, что коэффициент C меняется в значительных пределах и зависит от формы и размеров поперечного сечения потока и от шероховатости стенок.

Было предложено много формул для определения C, главным образом – эмпирических, т. е. базирующихся на экспериментальном материале.

Широко применяется, и хорошие результаты дает формула Н.Н.Павловского

.

(4.8)

Здесь n – коэффициент шероховатости, который берется по специальной шкале, y – показатель степени, зависящий от n и от R и колеблющийся от 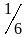до .

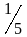Для формулы (4.8) составлены таблицы, дающие значение y или сразу C в зависимости от R и n.

В частности, положив в формуле (4.8) , получим формулу Маннинга:

.

(4.9)

Эта формула широко применяется при расчетах открытых потоков.

Удовлетворительные результаты дает формула А. А. Сабанеева

Здесь n берется по той же шкале шероховатости.

Нужно отметить, что все формулы для C применимы с достаточной надежностью для поверхностей с шероховатостью в пределах от n = 0,011 до n = 0,025.

Для очень гладких поверхностей (n < 0,01) и очень шероховатых (n > 0,025) формула Шези и другие, обычно используемые формулы, не дают соответствия характеру движения и механизму образования потерь.
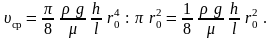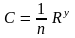