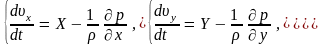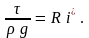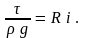18.Основное уравнение равномерного движения. Пьезометрический и гидравлический уклон

Для получения дифференциальных уравнений движения воспользуемся уравнениями равновесия Эйлера в виде (2.1), а также принципом Даламбера, который заключается в следующем: если в систему уравнений равновесия прибавить силы инерции, взятые с обратным знаком, то эти уравнения будут описывать уже процесс движения жидкости.

Силы давления и массовые силы в уравнениях Эйлера отнесены к единице массы. Если выражение для силы инерции отнести к единице массы, то получим в проекциях на оси координат

Тогда система дифференциальных уравнений движения невязкой жидкости, называемая также системой Эйлера, будет иметь вид

(3.10)

Напомним, что равномерное движение – это частный случай установившегося движения, характеризующийся тем, что по длине потока площадь трубы ω = const, а так как расход тоже постоянный, т. е. Q = const, то и скорость потока = const. Несмотря на такую, казалось бы, простоту, этот частный случай широко реализуется и для равномерных потоков в трубопроводах, и для неравномерного медленно меняющегося движения.

Рассмотрим равновесие отсека жидкости, движущейся в трубопроводе (рис. 3.18).

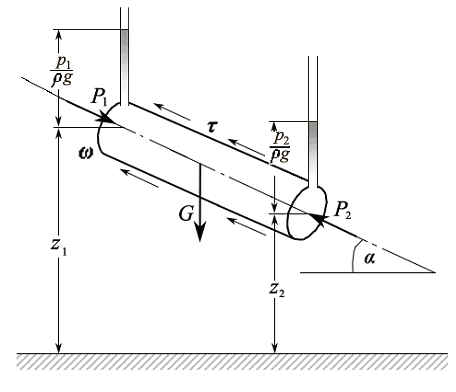
Рис. 3.18

Как известно, равномерное прямолинейное движение – это один из случаев равновесия. А согласно первому закону Ньютона, если тело находится в равновесии, то сумма всех сил, действующих на него, равна нулю.

Будем считать, что весь механизм трения сосредоточен на поверхности соприкосновения потока со стенками трубопровода, внутреннее трение в массиве жидкости учитывать не будем.

Тогда силы трения на стенках будут равны:

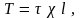
где τ – касательное напряжение трения;

– смоченный периметр;

l – длина рассматриваемого отсека.

Помимо сил трения на рассматриваемый отсек действуют силы давления P₁ и P₂ – по оси движения, а также сила тяжести жидкости в отсеке .

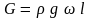Составим уравнение равновесия, т. е. равенства нулю сил, действую-щих на жидкость, в проекции на ось движения:

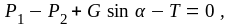
или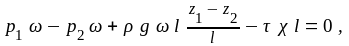

Где

Разделим это уравнение на 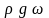. Получим:

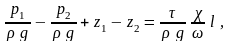
или

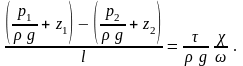
Левая часть равенства 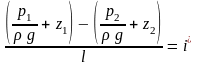– это пьезометри-ческий уклон. Отношение 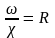– гидравлический радиус. Окончательно получаем

(3.11)

В случае равномерного движения пьезометрический уклон равен гидравлическому. Тогда получаем

(3.12)

Это и есть основное уравнение равномерного движения жидкости.

Падение полной энергии на единицу длины потока выражается формулой

и называется гидравлическим уклоном.

Следовательно, величина гидравлического уклона характеризует уменьшение полной удельной энергии потока на единицу длины.

Понятие уклона можно ввести и для пьезометрической линии, это будет пьезометрический уклон:

Пьезометрический уклон может быть как положительным, так и отрицательным. В частном случае равномерного движения, когда скорость по длине потока постоянна, очевидно, что i = i*. Такая картина имеет место, например, при напорном движении жидкости в трубах.

Положительные значения гидравлического и пьезометрического уклонов соответствуют падению полной энергии или пьезометрической линии.

При движении вязкой жидкости в трубах возникают дополнительные силы сопротивления. Частицы жидкости, прилегающие к поверхности трубы, тормозятся (прилипают). Из-за наличия вязкости такое торможение передается следующим слоям. В результате в трубе устанавливается распределение скорости движения жидкости, при котором скорость по мере удаления от оси трубы к стенкам постепенно уменьшается. Равнодействующая сил сопротивления направлена в сторону, противоположную движению, и параллельна направлению движения. Эта сила является силой гидравлического трения.

Для преодоления силы гидравлического трения и поддержания поступательного движения жидкости необходимо, чтобы на жидкость действовала сила, направленная в сторону ее движения и равная (или большая) силе сопротивления, т. е. необходимо затрачивать энергию. Энергия, необходимая для преодоления сил сопротивления, и есть потерянная энергия, учитываемая уравнением Бернулли.

Потери удельной энергии, их еще называют потери напора или гидравлические потери, зависят от формы и размеров русла, скорости течения, вязкости жидкости и шероховатости стенок трубопровода.