16. Уравнение Бернулли для целого потока реальной (вязкой)жидкости

17. Геом.Интерпретация ур-я Бернулли. Диаграмма Бернулл

При движении реальной вязкой жидкости в ней возникают силы трения. Часть энергии системы расходуется на преодоление сил трения, необратимым образом при этом преобразуясь в тепловую энергию. Тепловая энергия безвозвратно теряется – рассеивается в окружающее пространство. Поэтому, чтобы применить уравнение Бернулли к процессам в реальной жидкости, в уравнении сохранения энергии нужно учесть эти потери энергии.

Энергия потока в первом сечении

Энергия потока во втором сечении

Энергия потока во втором сечении будет меньше энергии в первом сечении как раз на величину потерь:

или

.

Если мы решим распространить уравнение Бернулли от элементарной струйки на целый поток, то нужно учитывать следующее обстоятельство. Удельную кинетическую энергию целого потока можно вычислить по формуле .

Здесь – средняя скорость в поперечном сечении потока.

В действительности скорости в поперечном сечении потока, как уже обсуждалось выше, существенно отличаются друг от друга: у стенок и дна они малы, к центру потока увеличиваются. Поэтому кинетическая энергия, рассчитанная по средней скорости потока, не равна сумме кинетических энергий элементарных струек, составляющих этот поток. Сумма энергий оказывается больше, и в первый член уравнения Бернулли приходится вводить поправочный коэффициент α, называемый коэффициентом кинетической энергии:

.

Так как – масса отдельных струек, а – масса всего потока жидкости, то имеем: .

Отметим, что чем больше – средняя скорость в сечении, тем коэффициент α ближе к единице.

В обычных условиях при турбулентном течении в трубах и открытых каналах α меняется в пределах 1,02 – 1,12, поэтому для турбулентных течений обычно принимают α ≈ 1,0.

Для ламинарных течений, имеющих большую неравномерность распределения скоростей по сечению, принимается, α = 2,0.

Что касается таких членов уравнения Бернулли как пьезометрический напор и геометрический напор z, то о них можно сказать следующее.

При распределении давления в поперечном сечении потока по гидростатическому закону можно отнести эти члены к любой точке потока в этом сечении, обычно их относят к центру тяжести. Предположение о гидростатическом законе распределения давления справедливо для параллельноструйного или плавно меняющегося движения и несправедливо в потоках, имеющих значительную кривизну. При значительной кривизне потока эти величины относятся к динамической оси потока, а при отклонении от оси необходимо вводить поправку, учитывающую влияние центробежных сил на распределение давления.

Таким образом, в случае параллельноструйного или плавно изменяющегося движения при обобщении уравнения Бернулли на целый поток реальной жидкости запись этих членов не изменяется. И тогда уравнение Бернулли для целого потока реальной (вязкой) жидкости при установившемся движении записывается в виде

или

(3.9)

В такой форме записи все члены уравнения Бернулли имеют линейную размерность, представляя собой напоры или высоты.

Попробуем представить уравнение Бернулли в виде линейной диаграммы (рис. 3.17).

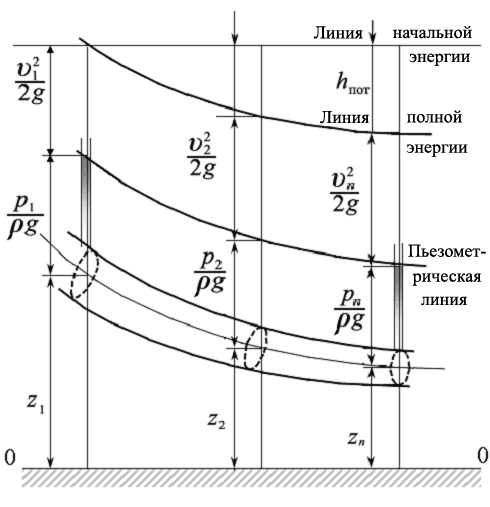
Рис. 3.17

Геометрический напор z отсчитывается от условной плоскости сравнения 0–0 до оси потока. Далее вверх откладываются отрезки, равные пьезометрическому напору и скоростному напору . Концы соответствующих отрезков в разных сечениях по длине потока соединяются линиями. Так получаются пьезометрическая линия и линия полной энергии. Константа в правой части уравнения Бернулли, характеризующая начальный запас энергии, соответствует горизонтальной линии начальной энергии. Расстояние между линиями начальной и полной энергии представляет собой потерянный напор .

Построенная диаграмма наглядно иллюстрирует преобразование удельной энергии потока при его движении, показывает переход одного вида энергии в другой. Так, например, при расширении поперечного сечения потока происходит увеличение потенциальной энергии давления (пьезометрического напора), а кинетическая энергия (скоростной напор) уменьшается. При уменьшении сечения наблюдаем обратную картину.

Важно заметить, что линия полной энергии для реальной жидкости может только падать по длине потока из-за непрерывного увеличения потерь. А пьезометрическая линия может повышаться и понижаться в зависимости от кинетической энергии потока.