Завдання№1

1. Обчислити визначник застосовуючи правило трикутника.

2. Обчислити визначник розклавши його по елементах 1-го рядка.

3. Обчислити визначник зробивши нулі у першому стовпці.

1. 2. 3. 4.

5. 6. 7. 8.

9. 10. 11. 12.

13. 14. 15. 16.

17. 18. 19. 20.

21. 22. 23. 24.

25. 26. 27. 28.

29. 30.

Завдання№2

Для даного визначника  знайти мінори й алгебраїчні доповнення елементів _i2 , _3j .

Обчислити визначник :

1. розклавши його по елементах i-го рядка;

2. розклавши його по елементах j-го стовпчика;

3. отримавши попередньо нулі в i-му рядку.

II. Варіанти

1. 2. 3. 4.

i=4, j=1 i=3, j=3 i=4,j=1 i=1, j=3

5. 6. 7. 8.

i=2, j=4 i=1,j=2 i=2, j=3 i=3, j=1

9. 10. 11. 12.

i=4, j=3 i=4, j=2 i=3, j=4 i=1, j=2

13. 14. 15. 16.

i=1, j=4 i=2, j=4 i=1, j=3 i=3, j=2

17.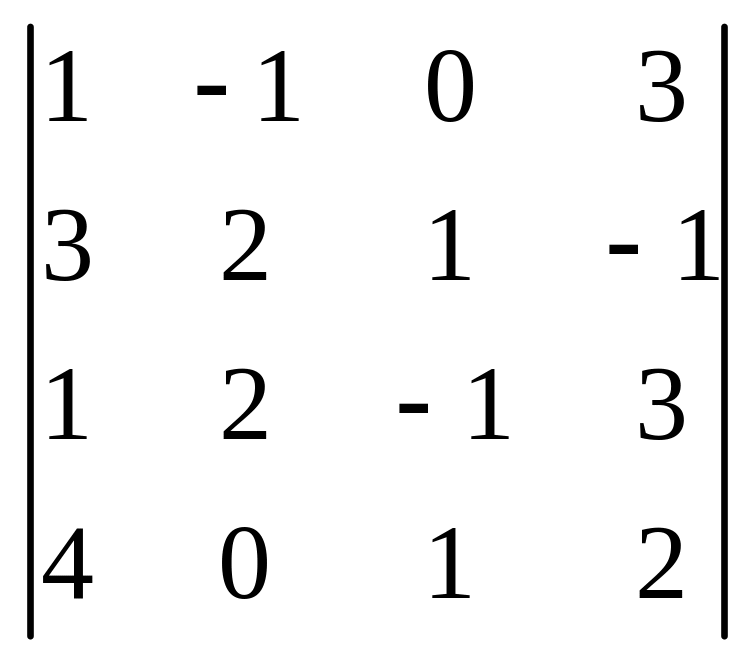 18. 19. 20.

i=3, j=1 i=2, j=4 i=2, j=3 i=4, j=3

21. 22. 23. 24.

i=1, j=2 i=3, j=2 i=3, j=2 i=4, j=4

25. 26. 27. 28.

i=2, j=3 i=4, j=1 i=1, j=2 i=3, j=4

29. 30.

i=4, j=4 i=2, j=2

Контрольні запитання.

1. Які властивості має визначник.

2. Сформулюйте теорему про розкладання визначника.

3. Що таке мінор?

4. Як вивизначити алгебраїчне доповнення елементів a_{i j} ?

ПРАКТИЧНА РОБОТА №2

Тема: Розв’язання матричних рівняннь. Дії над матрицями.

Мета: Навчитися знаходити обернену матрицю, перемножати матриці.

Короткі методичні вказівки:

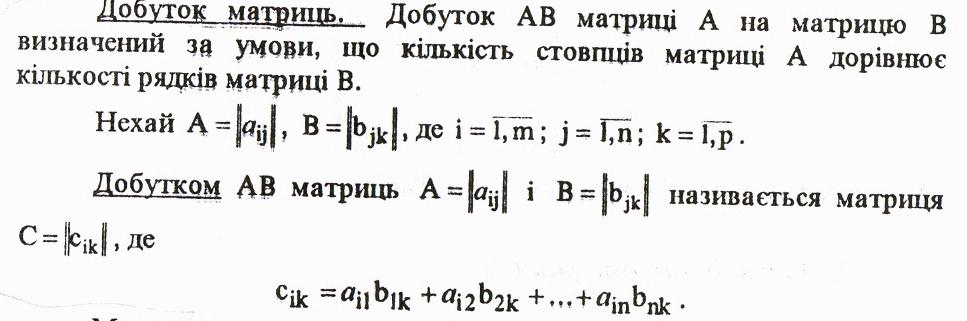
Розв’язок типового варіанту:

1. А= В=

В·А= = = ;

А·В= = = ;

2. Х=

А·Х=В , А= В=

А ·А· Х= А В Х= А · В.

Знайдемо А :

А= Запишемо алгебраічні доповнення до елементів матриці А .

А11 = -8 А12 = -10 А21 = 4 А22 = 6

Складаємо з них матрицю та транспонуємо її:

А* = А *=

Обчислимо:

= = -48+40=-8, тоді А = -

Перевіримо правильність знаходження оберненої матриці: А · А= Е.

- · = - = - =

Далі:

Х= А · В= - · =- = - = .

Відповідь:

Х= .

Індивідуальні завдання:

1. Знайти добуток матриць В·А та А·В.

2. Знайти А та А· А .

3. Розв’язати матричне рівняння .

1.1) А = В= 2) · Х=

2.1) А = В= 2) У· =

3.1) А = В= 2) ·Х=

4.1) А = В= 2) У· =

5.1) А = В= 2) ·Х=

6.1) А = В= 2) У· =

7.1) А = В= 2) ·Х=

8.1) А = В= 2) У· =

9.1) А = В= 2) ·Х=

10.1) А = В= 2) У· =

11.1) А = В= 2) ·Х=

12.1) А = В= 2) У· =

13.1) А = В= 2) ·Х=

14.1) А = В= 2) У· =

15.1)А = В= 2) ·Х=

16.1) А = В= 2) У· =

17.1) А = В= 2) ·Х=

18.1)А = В= 2) У· =

19.1)А = В= 2) ·Х=

20.1)А = В= 2) У· =

21.1) А = В= 2) ·Х =

22.1)А = В= 2) У· =

23.1)А = В= 2) ·Х =

24.1)А = В= 2)У· =

25.1)А = В= 2) ·Х =

26.1)А = В= 2) У· =

27.1) А = В= 2) ·Х =

28.1)А = В= 2)У· =

29.1)А = В= 2) ·Х =

30.1)А = В= 2) У· = .

Контрольні питання .

1. Згадайте різновиди матриць.

2. Як множити квадратні матриці.

3. Алгоритм знаходження оберненної матриці.

4. Чи комутативна операція множення на множинні матриць.

ПРАКТИЧНА РОБОТА №3

Тема: Однорідні та неоднорідні системи алгебраїчних рівнянь

Мета: Навчитися розв'язувати системи рівнянь застосовуючи методи Крамера, Гаусса та оберненої матриці

Короткі методичні вказівки:

Системою m лінійних рівнянь із n невідомими називається система виду

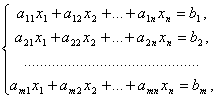
де a_ij й b_i (i=1,…,m; b=1,…,n)– деякі відомі числа, а x₁,…,x_n–невідомі. У позначенні коефіцієнтів a_ij перший індекс i означає номер рівняння, а другий j – номер невідомого, при якому стоїть цей коефіцієнт.

Коефіцієнти при невідомих будемо записувати у вигляді матриці 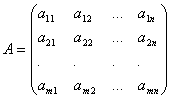, що назвемо матрицею системи.

Числа, що стоять у правих частинах рівнянь, b₁,…,b_m називаються вільними членами.

Сукупність n чисел c₁,…,c_n називається рішенням даної системи, якщо кожне рівняння системи звертається в рівність після підстановки в нього чисел c₁,…,c_n замість відповідних невідомих x₁,…,x_n...

Наша задача буде полягати в знаходженні рішень системи. При цьому можуть виникнути три ситуації:

1. Система може мати єдине рішення.

2. Система може мати нескінченну множину рішень. Наприклад, 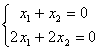. Рішенням цієї системи є будь-яка пара чисел, що відрізняються знайомий.

3. І третій випадок, коли система взагалі не має рішення. Наприклад, 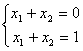, якби рішення існувало, то x₁ + x₂ рівнялося б одночасно нулю й одиниці.

Система лінійних рівнянь, що має хоча б одне рішення, називається сумісна. У противному випадку, тобто якщо система не має рішень, то вона називається несумісною.

МАТРИЧНИЙ МЕТОД РІШЕННЯ СИСТЕМ ЛІНІЙНИХ РІВНЯНЬ

Матриці дають можливість коротко записати систему лінійних рівнянь. Нехай дана система з 3-х рівнянь із трьома невідомими:

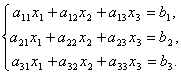
Розглянемо матрицю системи 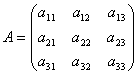й матриці стовпці невідомих і вільних членів

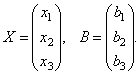
Знайдемо добуток

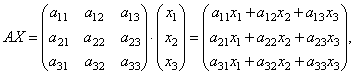
тобто у результаті добутку ми одержуємо ліві частини рівнянь даної системи. Тоді користуючись визначенням рівності матриць дану систему можна записати у вигляді

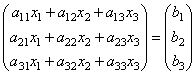або коротше A∙ X=B.

Тут матриці A й B відомі, а матриця X невідома. Її й потрібно знайти, тому що її елементи є рішенням даної системи. Це рівняння називають матричним рівнянням.

Нехай визначник матриці відмінний від нуля |A| ≠ 0. Тоді матричне рівняння вирішується таким способом. Помножимо обидві частини рівняння ліворуч на матрицю A^-1, зворотну матриці A: або . Оскільки A^-1A = E й E∙ X = X, то одержуємо рішення матричного рівняння у вигляді X = A^-1B.

Помітимо, що оскільки зворотну матрицю можна знайти тільки для квадратних матриць, то матричним методом можна вирішувати тільки ті системи, у яких число рівнянь збігається із числом невідомих. Однак, матричний запис системи можливий й у випадку, коли число рівнянь не дорівнює числу невідомих, тоді матриця A не буде квадратною й тому не можна знайти рішення системи у вигляді X = A^-1B.

ПРАВИЛО КРАМЕРА

Розглянемо систему 3-х лінійних рівнянь із трьома невідомими:

Визначник третього порядку, що відповідає матриці системи, тобто складений з коефіцієнтів при невідомих,

називається визначником системи.

Складемо ще три визначника в такий спосіб: замінимо у визначнику ∆ послідовно 1, 2 й 3 стовпці стовпцем вільних членів

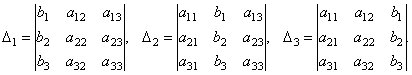
Тоді можна довести наступний результат.

Теорема (правило Крамера). Якщо визначник системи = 0, те розглянута система має одне й тільки одне рішення, причому

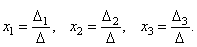
МЕТОД ГАУССА

Раніше розглянуті методи можна застосовувати при рішенні тільки тих систем, у яких число рівнянь збігається із числом невідомих, причому визначник системи повинен бути відмінний від нуля. Метод Гаусса є більше універсальним і придатний для систем з будь-яким числом рівнянь. Він полягає в послідовному виключенні невідомих з рівнянь системи.

Знову розглянемо систему із трьох рівнянь із трьома невідомими:

.

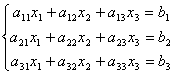Перше рівняння залишимо без зміни, а з 2-го й 3-го виключимо що складають, утримуючі x₁. Для цього друге рівняння розділимо на а₂₁ і помножимо на - а ₁₁, а потім складемо з 1-ым рівнянням. Аналогічно третє рівняння розділимо на а₃₁ і помножимо на - а ₁₁, а потім складемо з першим. У результаті вихідна система прийме вид:

Тепер з останнього рівняння виключимо доданок, що містить x₂. Для цього третє рівняння розділимо на , помножимо на й складемо із другим. Тоді будемо мати систему рівнянь:

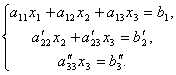
Звідси з останнього рівняння легко знайти x₃, потім з 2-го рівняння x₂ й, нарешті, з 1-го – x₁.

При використанні методу Гаусса рівняння при необхідності можна міняти місцями.Часто замість того, щоб писати нову систему рівнянь, обмежуються тим, що виписують розширену матрицю системи:

і потім приводять її до трикутного або діагонального виду за допомогою елементарних перетворень.

До елементарних перетворень матриці ставляться наступні перетворення:

1. перестановка рядків або стовпців;

2. множення рядка на число, відмінне від нуля;

3. додаток до одного рядка інші рядки.

СИСТЕМА ОДНОРІДНИХ ЛІНІЙНИХ РІВНЯНЬ

Системою однорідних лінійних рівнянь називається система виду

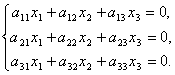
Ясно, що в цієї випадку , тому що всі елементи одного зі стовпців у цих визначниках дорівнюють нулю.

Тому що невідомі знаходяться по формулах , то у випадку, коли Δ ≠ 0, система має єдине нульове рішення x = y = z = 0. Однак, у багатьох задачах цікаве питання про те, чи має однорідна система рішення відмінні від нульового.

Теорема. Для того, щоб система лінійних однорідних рівнянь мала ненульове рішення, необхідно й досить, щоб визначник = 0.

Отже, якщо визначник = 0, то система має єдине рішення. Якщо ж ≠ 0, то система лінійних однорідних рівнянь має нескінченну множину рішень.

Розв'язок типового варіанту:

1. Розв'язати систему

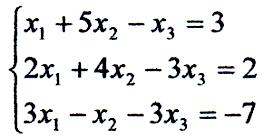
Перевіримо сумісність. Знайдемо ранг матриці

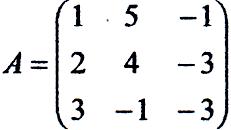
даної системи і ранг розширеної матриці системи

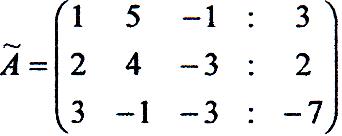
Для цього домножимо перший рядок матриці А на (- 2) і складемо з другим, після цього доножимо перший рядок на (-3) і складемо з третім; змінимо місцями другий і третій стовбці.

Отримаємо:

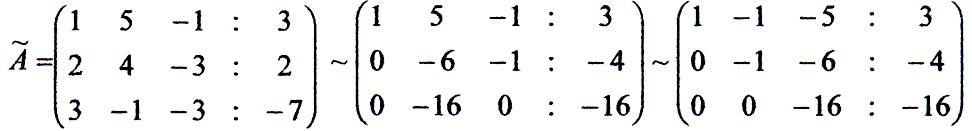
Отже, rang A = rang A = 3 (числу невідомих). Значить, вхідна система сумісна виз.(має єдине рішення).

а) За формулами Крамера

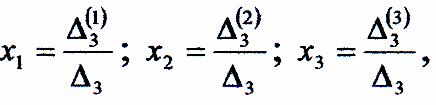
Де

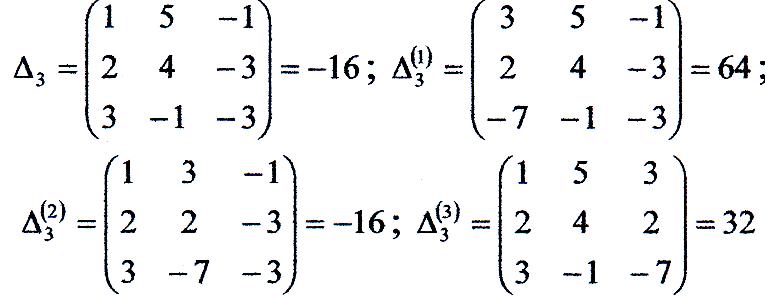
Знаходимо:

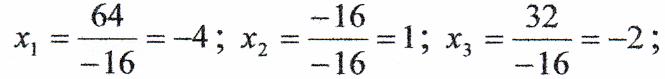
б) для знаходження рішення системи за допомогою оберненої матриці запишемо систему рівнянь в матричній формі А • X = В . Рішення системи в матричній формі має вигляд X = • В . По формулі знаходимо обернену матрицю (вона існує, бо Д, = detА = -16 ≠ 0);

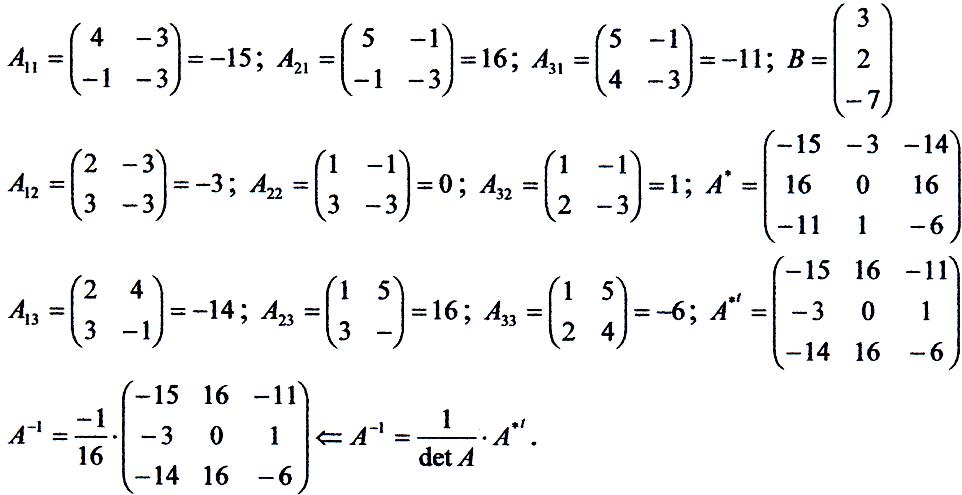
Рішення системи:

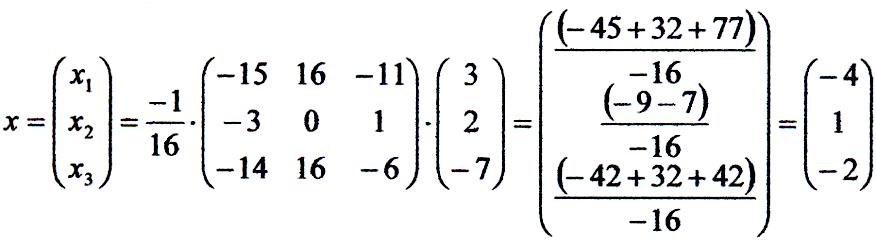
Отже,

в) вирішимо систему методом Гаусса. Записуємо систему, яка відповідає приведеній матриці А:

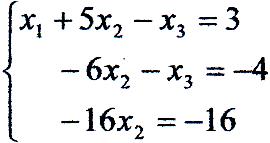
З отриманої системи знаходимо: (зворотній хід по Гауссу).

2. Дано систему лінійних неоднорідних алгебраїчних рівнянь:

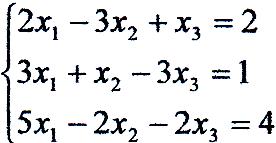
Перевірити, чи сумісна система; в випадку сумісності вирішити її:

а) за формулами Крамера;

б) за допомогою оберненої матриці( матричним методом);

в) методом Гаусса.

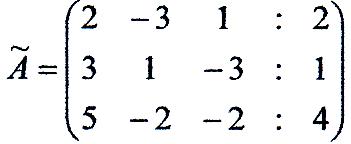
Міняємо третій і перший стовбці місцями; умножаємо перший рядок на 3 і додаємо до другого; умножаємо перший рядок на 2 і додаємо до третього; з третього рядка віднімаємо другий:

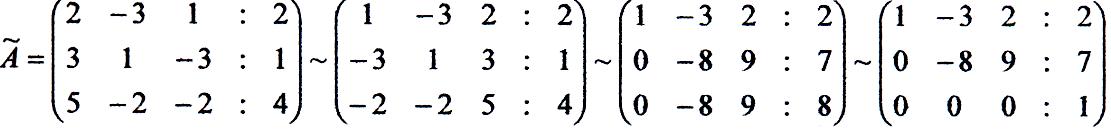
Тепер, ясно, що rang А = 2, rang Ã= 3. Згідно теоремі Кронекера-Капеллі, з того що rang А ≠ rang à , слідує несумісність вхідної системи.

3. Вирішити однорідну систему лінійних алгебраїчних рівнянь:

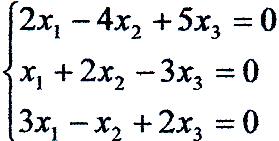
Визначник системи:

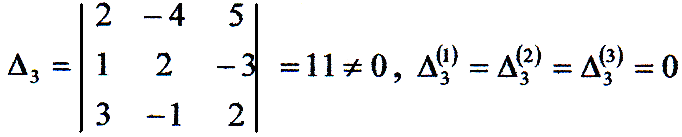
Тому система має єдине нульове рішення:

4. Вирішити однорідну систему лінійних алгебраїчних рівнянь:

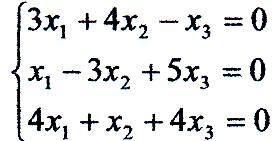
Так як:

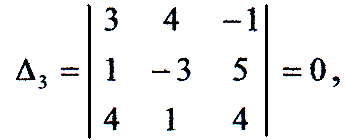
то система має безліч рішень. Оскільки rang А = 2 < п = 3, візьмемо будь які два рівняння системи (наприклад, перше і друге) і знайдемо її рішення. Маємо:

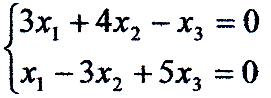
Так як визначник з коефіцієнтів при невідомих х, і х₂ не дорівнює нулю, то за базисні невідомі візьмемо x₁, і х₂ (хоча можна брати і інші пари невідомих) і перенесемо члени з x₃, в праві частини рівнянь:

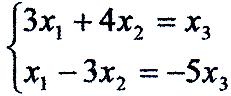
Вирішуємо останню систему по формулам Крамера:

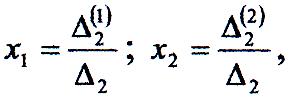
де :

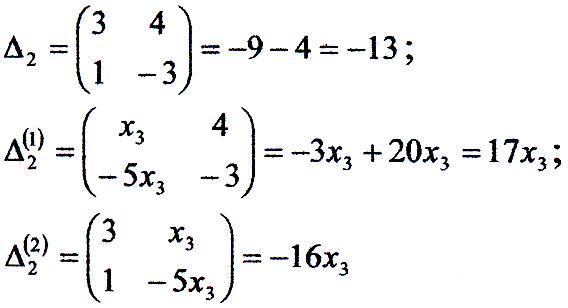
Звідси знаходимо, що:

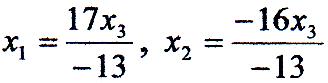
Вважаючи:

,де

k — довільний коефіцієнт пропорційності, одержуємо рішення вхідної системи:

Індивідуальні завдання:

1. Перевірити сумісність систем та у випадку сумісності розв'язати її:

а) за формулами Крамера

б) за допомогою оберненої матриці;

в) методом Гаусса.

2. Розв'язати однорідну систему рівнянь.

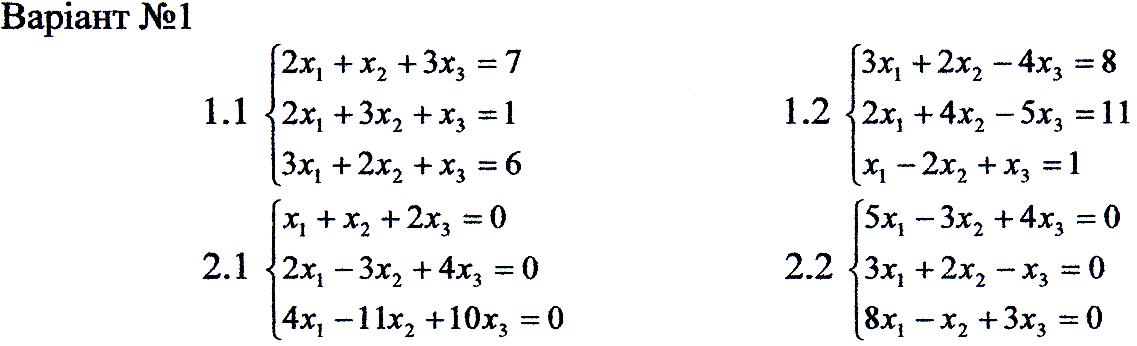
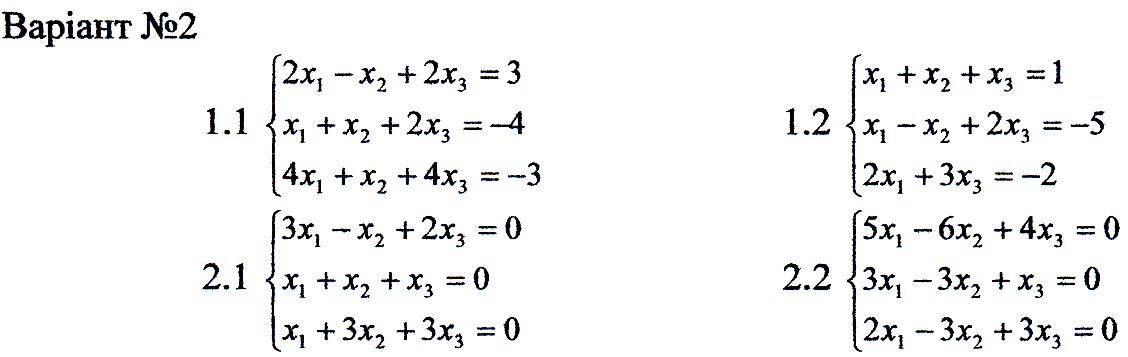
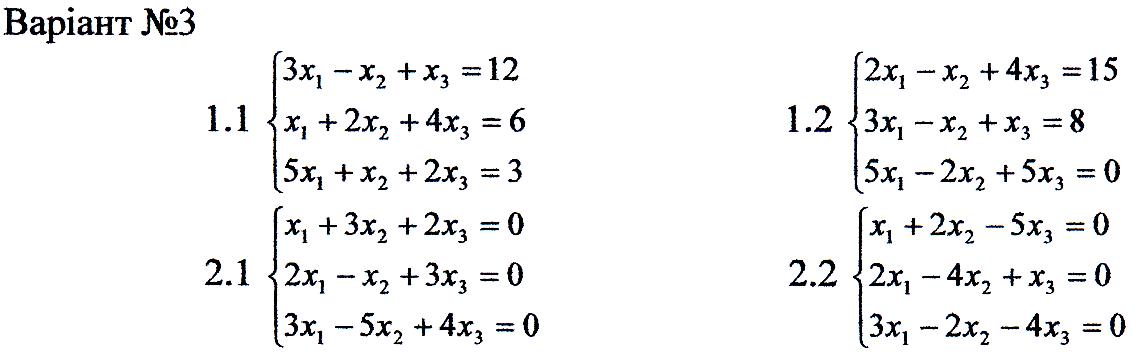
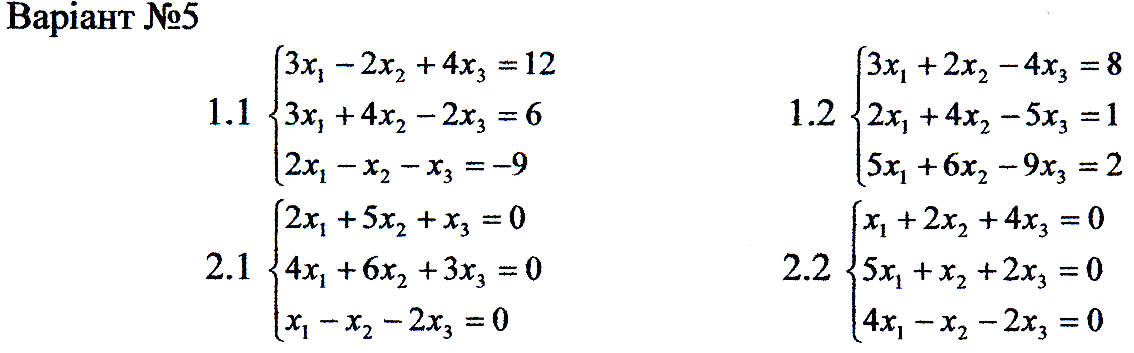
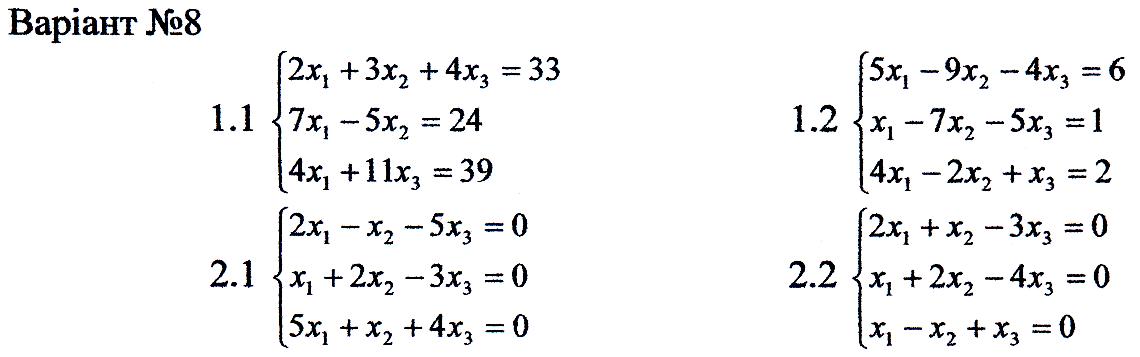
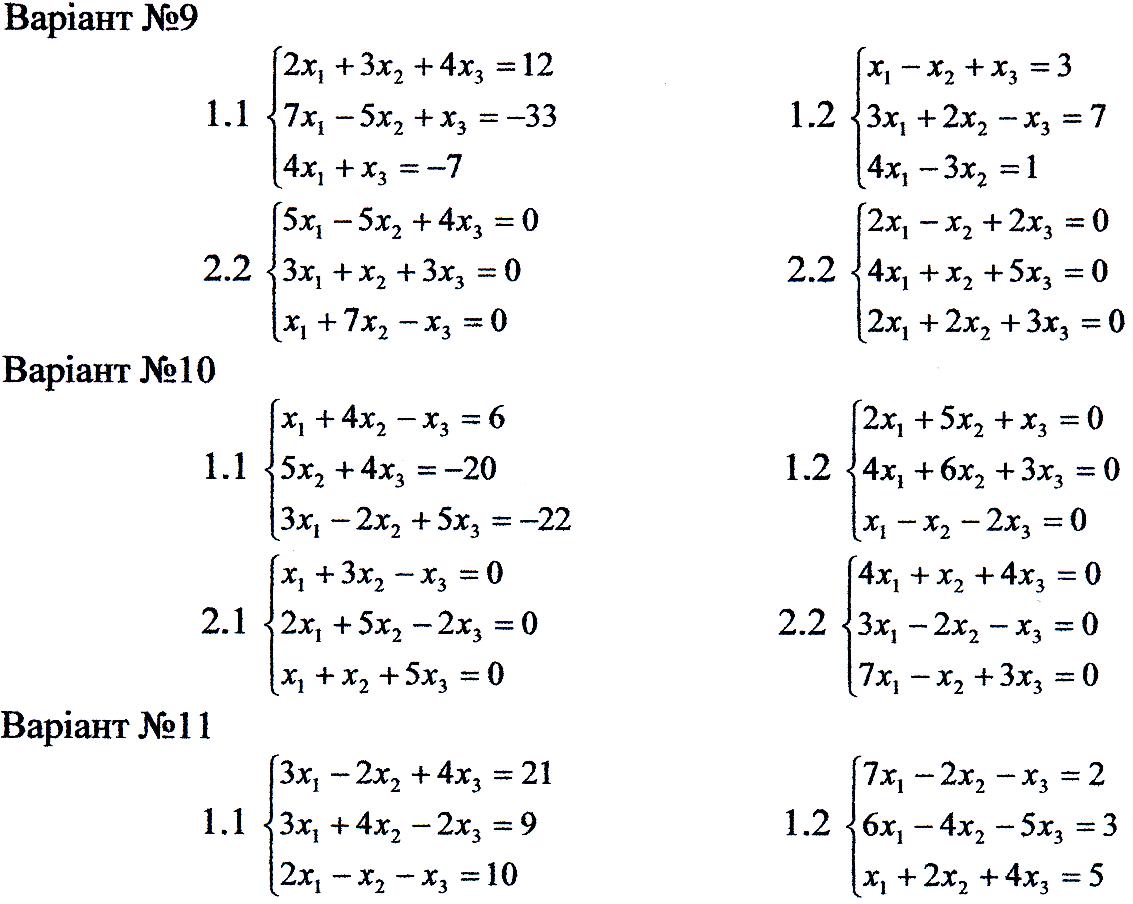
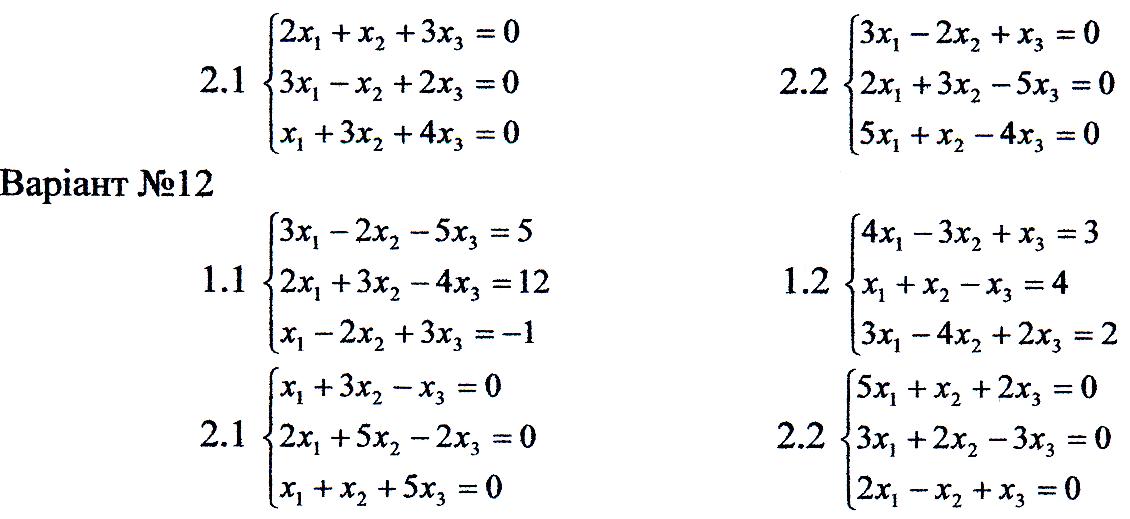
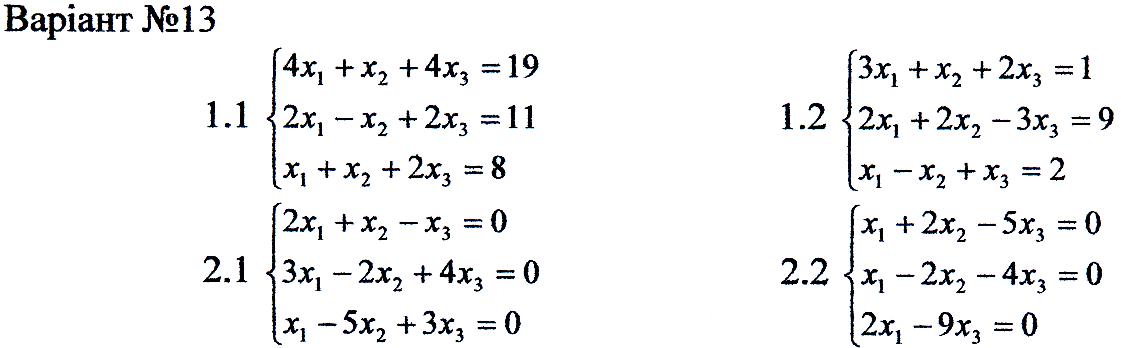
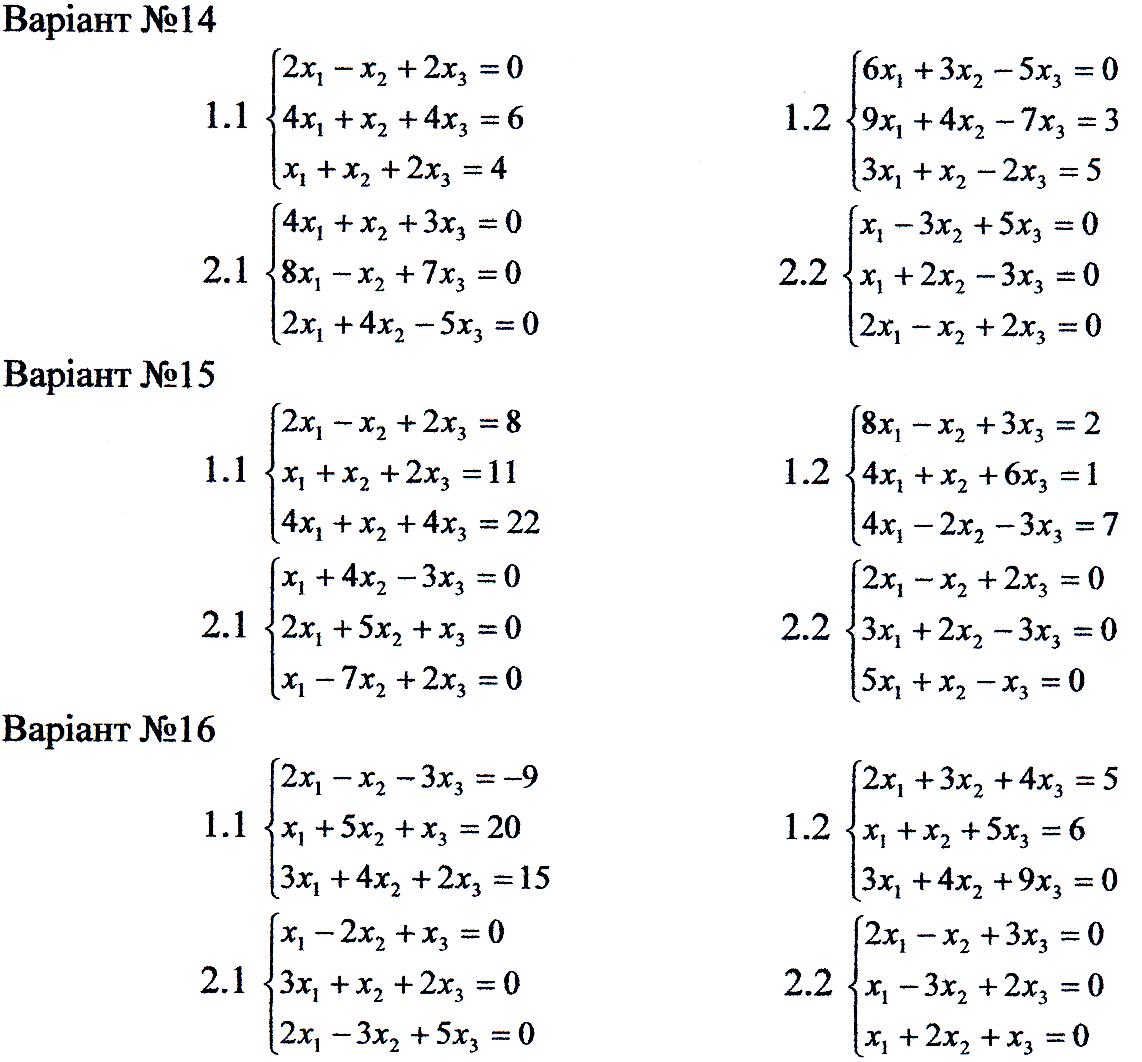
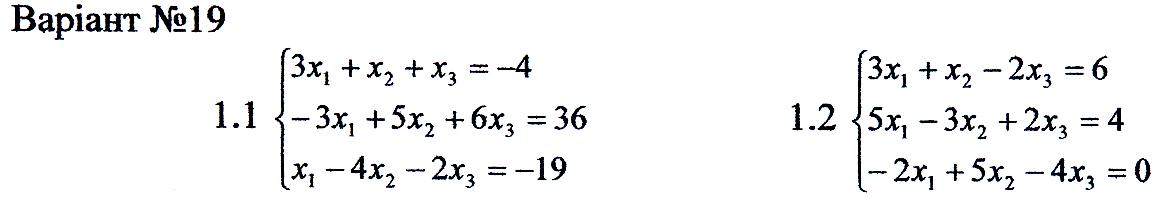
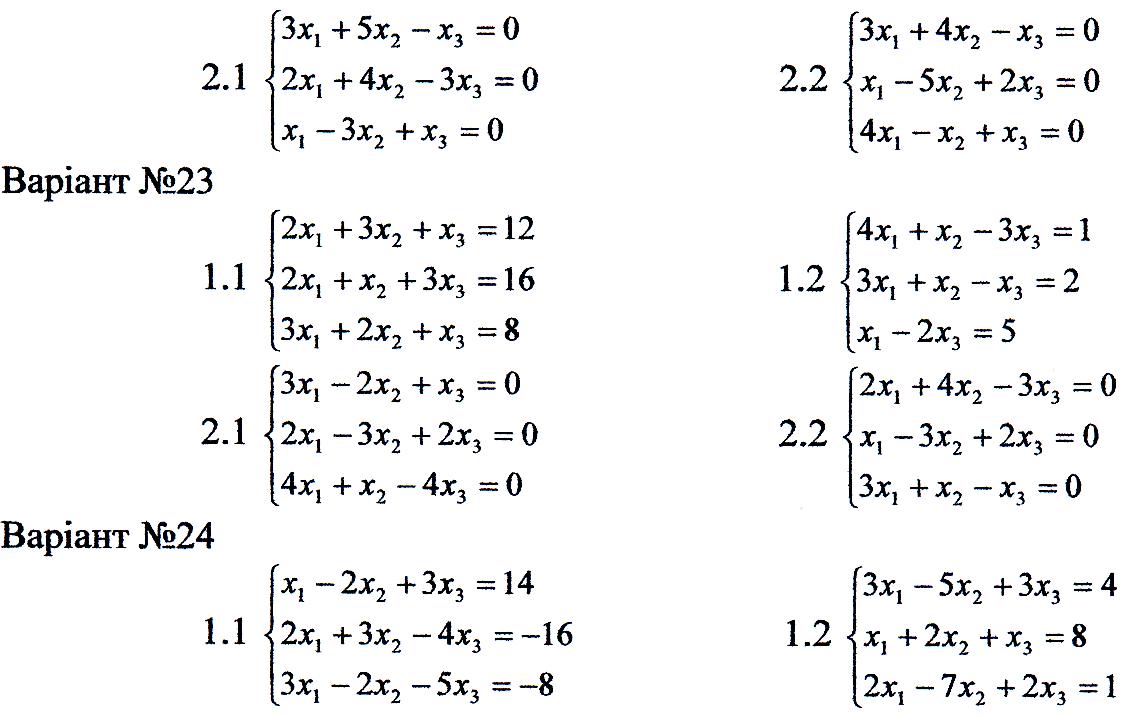
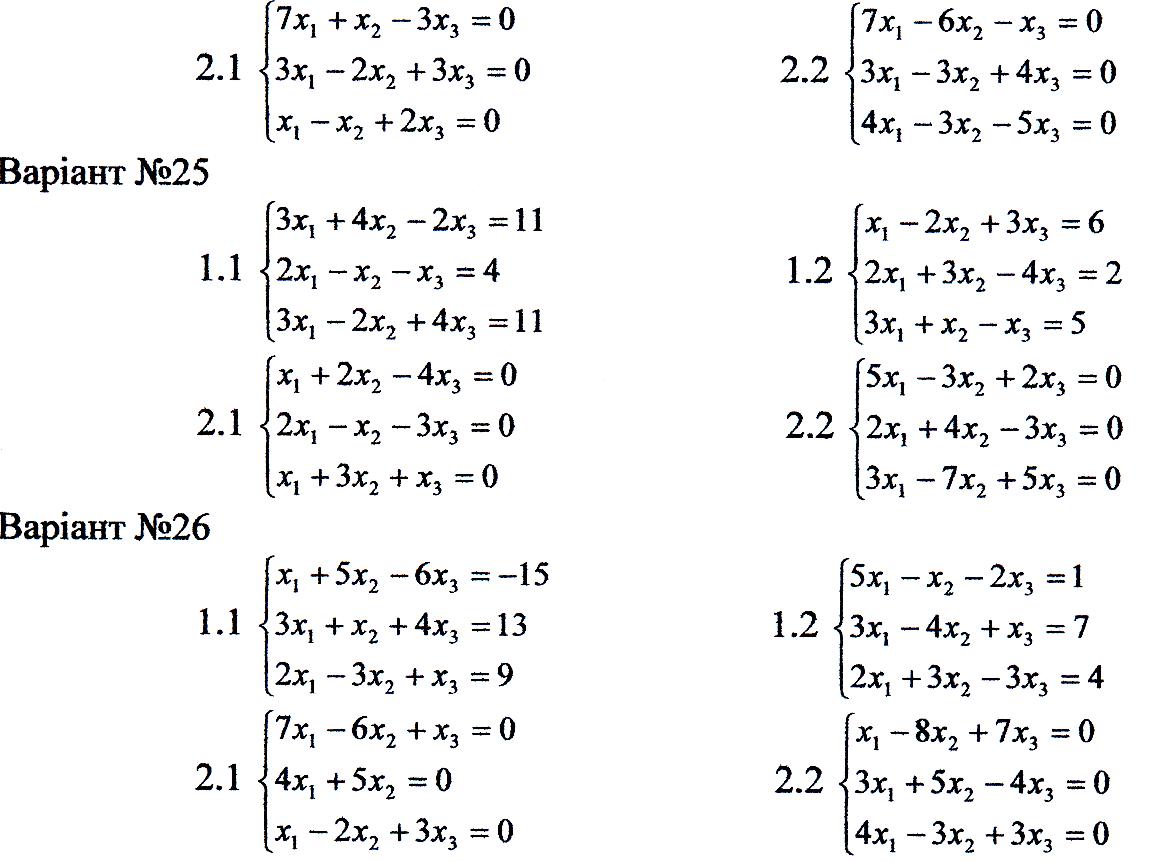
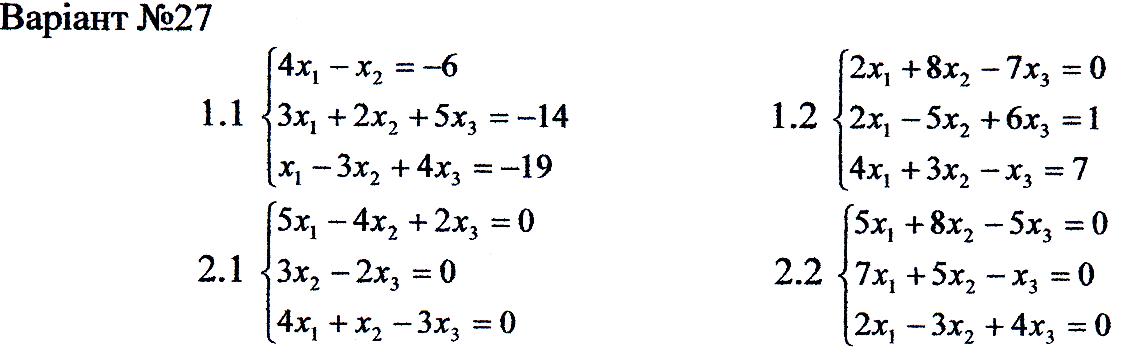
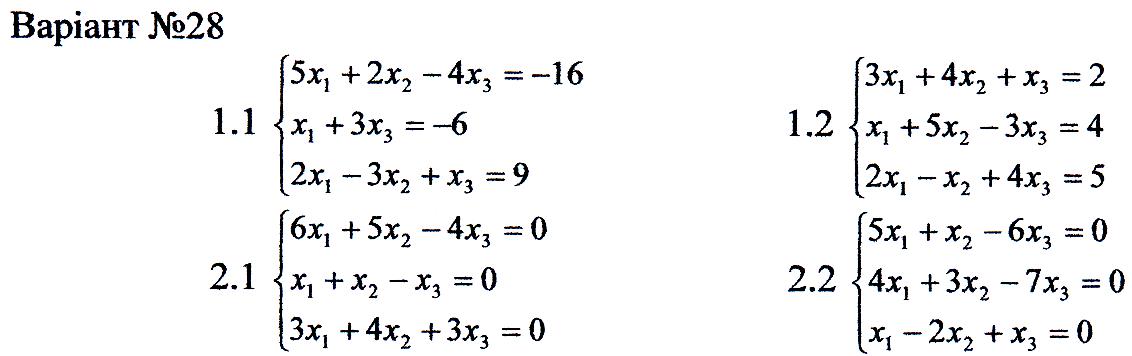
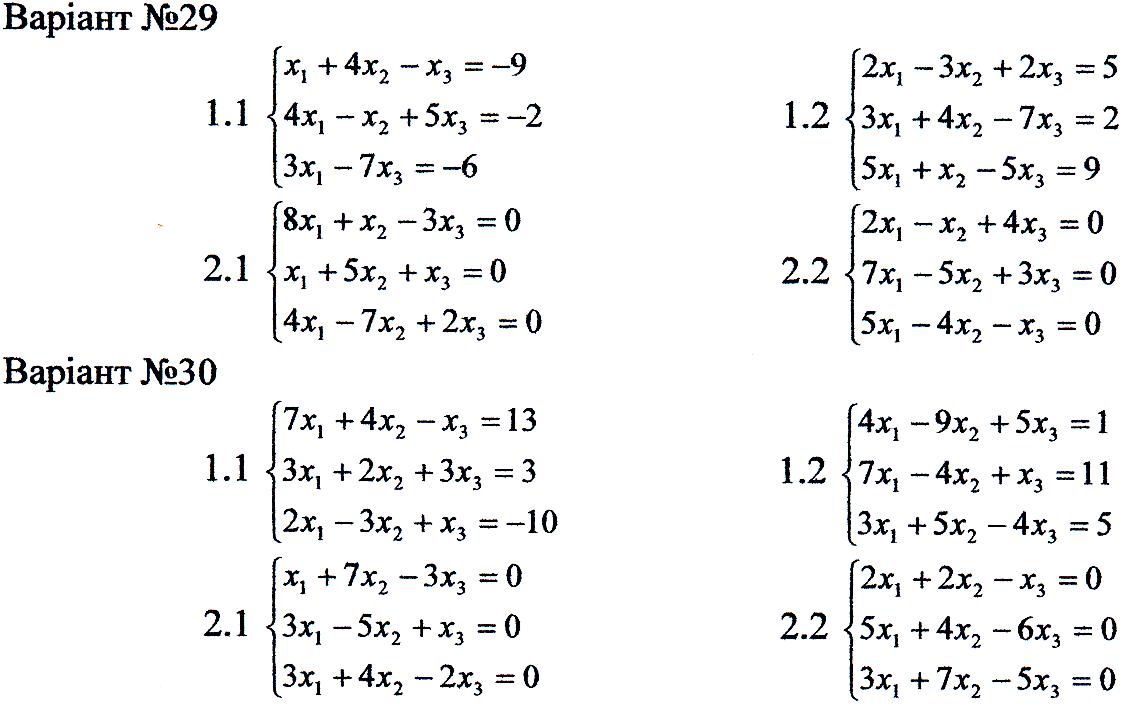
Контрольні запитання:

1. Означення системи лінійних алгебраїчних рівнянь

2. Теорема Кронекера-Капеллі (критерій сумісності системи).

3. Метод розв'язування СЛАР:

а) метод Крамера;

б) матричний метод;

в) метод Гаусса.

Практична робота №4

Тема : Векторний та змішаний добуток

Мета: Навчитися використовувати векторний та змішаний добуток до розв’язування задач .

Рішення типового варіанту.

1. Дані вектори а= 4i+4k, b=-i+3j+2k і c=3i+5j;

Знайти: а) визначити добуток векторів а,b,5c;

б) знайти модуль векторного добутку 3с і b;

в) визначити скалярний добуток двох векторів а і 3b;

г) перевірити ,чи будуть колєніарні або ортогональні два вектора а і b;

д) перевірити ,чи будуть компланарні три вектори а, b i c.

а) Так як 5c=15i+25j , то

(ax)*5c= = -100 -180 -200= -480;

б) Поскільки 3с=9i+15, то

3c*b = =30i+27+15k-18j+42,

= = ;

в) Знаходим : 3b=-3i+9j+6k, a*3b=4(-3)+0*9+4*6=12;

г) Так як a= (4,0,4), b=(-1,3,2) i 4/-1 0/3=4/2, то вектори а і b не колєніарні . Поскільки

a*b=4(-1)+0*3+4*2=0,

то вектори a i b не ортогональні;

д) вектори a,b,c компланарні , або abc=0. Знаходимо

abc=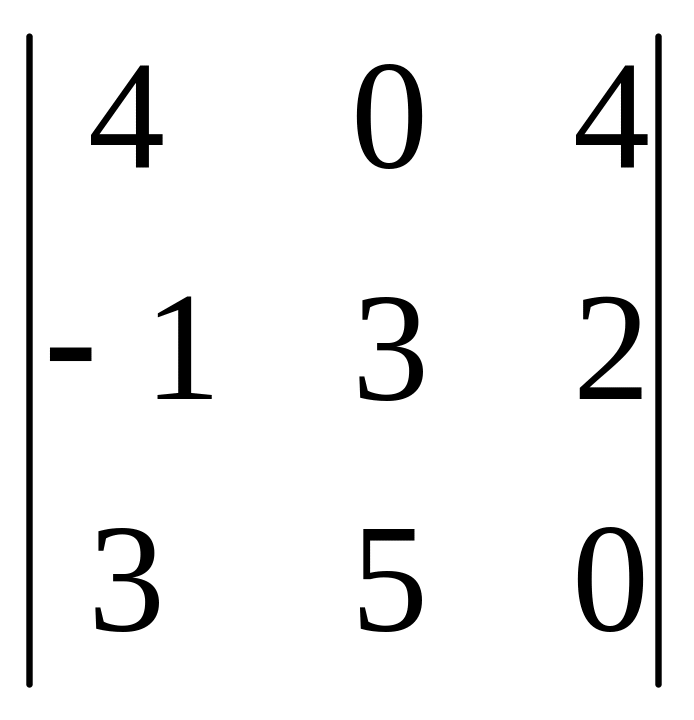 = -20-36-40=0;

вектори a,b і с компланарні.

2. Вершини піраміди знаходяться в крапках A(2,3,4), B(4,7,3), C(1,2,2) і D(-2,0,-1).

Знайти: а) площу грані АВС,

б) площу січення проходящу через середину ребер АВ, АС, АD,

в) об’єм піраміди ABCD.

a) S = Знаходим :

АВ=(2,4,-1), АС=(-1,-1,-2),

АВХАС= = -9i +5j +2k.

Маємо:

SABC= 1/2 =1/2 ;

а) Середні ребра АВ, ВС і AD знаходяться у крапках К(3;5;3,5), M(1,5; 2,5 ;3),

N( 0;1,5; 1,5).

Далі маємо:

S =1/2 , KM= (-1,5; -2,5; -0,5), KN (-3;-3,5; -2),

KMXKN= = 3,25i -1,5-2,25k,

S =1/2 =1/2

в) Поскільки V .=1/6 , AD= (-4 , -3, -5),

(ABXAC)· AD= =11,

то V= 11/6.

2. Сила F =(2,3,-5) прикладина до крапки А (1,-2,2).

Розрахувати : а) працю сили F в випадку, коли крапка її прикладення , рухаючись прямолінійно, переміщається із положення А в положення В (1,4,0);

б) модуль моменту сили F відносно крапки В.

а) Так як А= F ·s , s= AB=(0,6,-2), то F · AB= 2·0+3·6+(-5)(-2)=28, A=28;

б) Момент сили М=BA·F, BA=(0,-6,2),

BAXF= = 24i+4j+12k.

= =4 .

1. Дано вектори а, b и с .

Необхідно : а) визначити змішаний добуток трьох векторів;

б) знайти модуль векторного добутку;

в) визначити скалярний добуток двох векторів

г) перевірити, чи будуть коленіарні або ортогональні два вектора;

д) перевірити, чи будуть компланарні три вектора.

1.1 . a=2i-3j+k, b=j+4k, c=5i+2j-3k; a) a, 3b, c ; б) 3a,2c; в)b, -4c ; г) a, c; д) a,2b,3c.

(Відповідь: a) -261; б) ; в) 40.)

1.2 . a=3i+4j+k, b=i-2j+7k, c=3i-6j+21k; a) 5a, 2b, c ; б) 4b,2c; в)a, c ; г) b, c;

д) 2a,-3b, c.

(Відповідь: a) 0; б) 0 ; в) 6.)

1.3 . a=2i-4j-2k, b=7i+3j, c=3i+5j-7k; a) a, 2b, 3c ; б) 3a,-7b; в)c, -2a ; г) a, c;

д) 3a,2b,3c.

(Відповідь: a) -1840; б) ; в) 0.)

1.4 . a=-7i+2k, b=2i-6j+4k, c=i-3j+2k; a) a, -2b, -7c ; б) 4b,3c; в)2a, -7c ; г) b, c;

д) 2a,4b,3c.

(Відповідь: a) 0; б) 0 ; в) 42.)

1.5 . a=-4i+2j-k, b=3i+5j-2k, c=j+5k; a) a, 6b, 3c ; б) 2b,a; в)a, -4c ; г) a, b; д) a,6b,3c.

(Відповідь: a) -2538; б) ; в) 12.)

1.6 . a=3i-2j+k, b=2j-3k, c=-3i+2j-k; a) a, -3b, 2c ; б) 5a,3c; в)-2a, 4b ; г) a, c;

д) 5a,4b,3c.

(Відповідь: a) 0; б) 0 ; в) 56.)

1.7 . a=4i-j+3k, b=2i+3j-5k, c=7i+2j+4k; a) 7a, -4b, 2c ; б) 3a,5c; в)2b, 4c ; г) b, c;

д) 7a,2b,5c.

(Відповідь: a) -4480; б) ; в) 0.)

1.8 . a=4i+2j-3k, b=2i+k, c=-12i-6j+9k; a) 2a, 3b, c ; б) 4a,3b; в)b, -4c ; г) a, c;

д) 2a,3b,-4c.

(Відповідь: a) 0; б) ; в) 60.)

1.9 . a=-i+5k, b=-3i+2j+2k, c=-2i-4j+k; a) 3a, -4b, 2c ; б) 7a,-3c; в)2b, 3a ; г) b, c;

д) 7a,2b,-3c.

(Відповідь: a) -1680; б) ; в) 78.)

1.10 . a=6i-4j+6k, b=9i-6j+9k, c=i-8k; a) 2a, -4b, 3c ; б) 3b,-9c; в)3a, -5c ; г) a, b;

д) 3a,-4b,-9c.

(Відповідь: a) 0; б) ; в) 630.)

1.11 . a=5i-3j+4k, b=2i-4j+2k, c=3i+5j-7k; a) a, -4b, 2c ; б) -2b,4c; в)-3a, 6c ; г) b, c; д) a,-2b,6c.

(Відповідь: a) -464; б) ; в) 504.)

1.12 . a=-4i+3j-7k, b=4i+6j-2k, c=6i+9j-3k; a) -2a, b, -2c ; б) 4b,7c; в)5a, -3b ; г) b, c; д) -2a,4b,7c.

(Відповідь: a) 0; б) 0 ; в) -240.)

1.13 . a=-5i+2j-2k, b=7i-5k, c=2i+3j-2k; a) 2a, 4b, -5c ; б) -3b,11c; в)8a, -6c ; г) a, c;

д) 8a,-3b,11c.

(Відповідь: a) 4360; б) ; в) 0.)

1.14 . a=-4i-6j+2k, b=2i+3j-3k, c=-i+5j-k; a) 5a, 7b, 2c ; б) -4b,11a; в)3a, -7c ; г) a, b; д) 3a,7b,-2c.

(Відповідь: a) 0; б) 0 ; в) 672.)

1.15 . a=-4i+2j-3k, b=-3j+5k, c=6i+6j-4k; a) 5a, -b, 3c ; б) -7a,4c; в)3a, 9b ; г) a, c; д) 3a,-9b,4c.

(Відповідь: a) -1170; б) 56 ; в) 567.)

1.16 . a=-3i+8j, b=2i+3j-2k, c=8i+12j-8k; a) 4a, -6b, 5c ; б) -7a,9c; в)3b, -8c ; г) b, c; д) 4a,-6b,9c.

(Відповідь: a) 0; б) 252 ; в) -1632.)

1.17 . a=2i-4j-2k, b=9i+2k, c=3i+5j-7k; a) 7a, 5b, -c ; б)-5a,4b; в)3b, -8c ; г) a, c; д)7a,5b,-c.

(Відповідь: a) -10430; б) ; в) 984.)

1.18 . a=9i-3j+k, b=3i-15j+21k, c=i-5j+7k; a) 2a, -7b, 3c ; б) -6a,4c; в)5b, 7a ; г) b, c; д) 2a,-7b,4c.

(Відповідь: a)0; б) ; в) 3255.)

1.19 . a=-2i+4j-3k, b=5i+j-2k, c=7i+4j-k; a) a, -6b, 2c ; б) -8b,5c; в)-9a, 7c ; г) a, b; д) a,-6b,5c.

(Відповідь: a) 1068; б) ; в) -315.)

1.20 . a=-9i+4j-5k, b=i-2j+4k, c=5i+10j-20k; a) -2a, 7b, 5c ; б) -6b,7c; в)9a, 4c ; г) b, c; д) -2a,7b,4c.

(Відповідь: a) 0; б) ; в) 6660.)

1.21 . a=2i-7j+5k, b=-i+2j-6k, c=3i+2j-4k; a) -3a, 6b, -4c ; б) 5b,3c; в)7a, -4b ; г) b, c; д) 7a,-4b,3c.

(Відповідь: a) 2196; б) ; в) 1288.)

1.22 . a=7i-4j-5k, b=i-11j+3k, c=5i+5j+3k; a) 3a, -7b, 2c ; б) 2b,6c; в)-4a, -5c ; г) a, c; д) -4a,2b,6c.

(Відповідь: a) 28728; б) ; в) 0.)

1.23 . a=4i-6j-2k, b=-2i+3j+k, c=3i-5j+7k; a) 6a, 3b, 8c ; б) -7b,6a; в)-5a, 4c ; г) a, b; д) -5a,3b,4c.

(Відповідь: a) 0; б) 0; в) -560.)

1.24 . a=3i-j+2k, b=-i+5j-4k, c=6i-2j+4k; a) 4a, -7b, -2c ; б) 6b,4c; в)-2a, 5b ; г) a, c; д) 6a,-7b,-2c.

(Відповідь: a) 0; б) 0; в)160.)

1.25 . a=-3i-j-5k, b=2i-4j+8k, c=3i+7j-k; a) 2a, -b, 3c ; б) -9a,4c; в)5b, -6c ; г) b, c; д) 2a,5b,-6c.

(Відповідь: a) 0; б) ; в) 900.)

1.26 . a=-3i+2j+7k, b=i-5k, c=6i+4j-k; a) -2a, b, 7c ; б) 5a,-2c; в)3b, c ; г) a, c; д) -2a,3b,7c.

(Відповідь: a) 1260; б) 10 ; в) 33.)

1.27 . a=3i-j+5k, b=2 i -4 j +6 k, c=i-2j+3k; a) 3a, 4b, -5c ; б) 6b,3c; в) a, 4c ; г) b, c; д) -3a,4b,-5c.

(Відповідь: a) 0; б) 0; в) 80.)

1.28 . a=4i-5j-4k, b=5i-j, c=2i+4j-3k; a) a, 7b, -2c ; б) -5a,4b; в)8c, -3a ; г) a, c; д) -3a,4b,8c.

(Відповідь: a)2114; б) 20 ; в) 0.)

1.29 . a=-9i+4k, b=2i-4j+6k, c=3i-6j+9k; a) 3a, -5b, -4c ; б) 6b,2c; в)-2a, 8c ; г) b, c; д) 3a,6b,-4c.

(Відповідь: a) 0; б) 0; в) -144.)

1.30 . a=5i-6j-4k, b=4i+8j-7k, c=3j-4k; a) 5a, 3b, -4c ; б) 4b,a; в)7a, -2c ; г) a, b; д) 5a,4b,-2c.

(Відповідь: a) 11940; б)4 ; в) 28.)

2. Вершини піраміди знаходяться в крапках А,BC і D.

Знайти : а) площу вказаної грані;

б) площу січення проходящу через середину ребра L і дві вершини піраміди ;

в) об’єм піраміди ABCD.

2.1. A(3,4,5,), B (1,2,1), C(-2,-3,6), D(3,-6,-3); a)ACD; б)L=AB, C і D.

(Відповідь: a) ; б) ; в) 42.)

2.2. A(-7,-5,6,), B (-2,5,-3), C(3,-2,4), D(1,2,2); a)BCD; б)L=CD, A і B.

(Відповідь: a) ; б) ; в) 77/3.)

2.3. A(1,3,1,), B (-1,4,6), C(-2,-3,4), D(3,4,-4); a)ACD; б)L=BC, A і D.

(Відповідь: a) ; б) ; в) 3.)

2.4. A(2,4,1,), B (-3,-2,4), C(3,5,-2), D(4,2,-3); a)ABD; б)L=AC, B і D.

(Відповідь: a) ; б) ; в) 25/3.)

2.5. A(-5,-3,-4,), B (1,4,6), C(3,2,-2), D(8,-2,4); a)ACD; б)L=BC, A і D.

(Відповідь: a) ; б) ; в) 304/3.)

2.6. A(3,4,2,), B (-2,3,-5), C(4,-3,6), D(6,-5,3); a)ABD; б)L=BD, A і C.

(Відповідь: a) ; б) ; в) 40.)

2.7. A(-4,6,3,), B (3,-5,1), C(2, 6, -4), D(2,4,-5); a)ACD; б)L=AD, B і C.

(Відповідь: a) ; б) ; в) 100/3.)

2.8. A(7,5,8,), B (-4,-5,3), C(2,-3,5), D(5,1,-4); a)BCD; б)L=BC, A і D.

(Відповідь: a) ; б) ; в) 202/3.)

2.9. A(3,-2,6,), B (-6,-2,3), C(1,1,4), D(4,6,-7); a)ABD; б)L=BD, A і C.

(Відповідь: a) ; б) ; в) 52.)

2.10. A(-5,-4,-3,), B (7,3,-1), C(6,-2,0), D(3,2,-7); a)BCD; б)L=AD, B і C.

(Відповідь: a) ; б) ; в) 44.)

2.11. A(3,-5,-2,), B (-4,2,3), C(1,5,7), D(-2,-4,5); a)ACD; б)L=BD, A і C.

(Відповідь: a) ; б) ; в) 202/3.)

2.12. A(7,4,9,), B (1,-2,-3), C(-5,-3,0), D(1,-3, 4); a)ABD; б)L=AB, C і D.

(Відповідь: a) ; б) ; в) 50.)

2.13. A(-4,-7,-3,), B (-4,-5,7), C(2,-3,3), D(3,2,1); a)BCD; б)L=BC, A і D.

(Відповідь: a) ; б) ; в) 148/3.)

2.14. A(-4,-5,-3,), B (3,1,2), C(5,7,-6), D(6,-1,5); a)ACD; б)L=BC, A і D.

(Відповідь: a) ; б) ; в) 46.)

2.15. A(5,2,4,), B (-3,5,-7), C(1,-5,8), D(9,-3,5); a)ABD; б)L=BD, A і C.

(Відповідь: a) ; б) ; в) 286/3.)

2.16. A(-6,4,5,), B (5,-7,3), C(4,2,-8), D(2,8,-3); a)ACD; б)L=AD, B і C.

(Відповідь: a) ; б) ; в) 150.)

2.17. A(5,3,6,), B (-3,-4,4), C(5,-6,8), D(4,0,-3); a)BCD; б)L=BC, A і D.

(Відповідь: a) ; б) ; в) 332/3.)

2.18. A(5,-4,4,), B (-4,-6,5), C(3,2,-7), D(6,2,-9); a)ABD; б)L=BD, A і C.

(Відповідь: a) ; б) ; в) 82/3.)

2.19. A(-7,-6,-5,), B (5,1,-3), C(8,-4,0), D(3,4,-7); a)BCD; б)L=AD, B і C.

(Відповідь: a) ; б) ; в) 86/3.)

2.20. A(7,-1,-2,), B (1,7,8), C(3,7,9), D(-3,-5,2); a)ACD; б)L=BD, A і C.

(Відповідь: a) ; б) ; в) 124/3.)

2.21. A(5,2,7,), B (7,-6,-9), C(-7,-6,3), D(1,-5,2); a)ABD; б)L=AB, C і D.

(Відповідь: a) ; б) ; в) 76.)

2.22. A(-2,-5,-1,), B (-6,-7,-9), C(4,-5,1), D(2,1,4); a)BCD; б)L=BC, A і D.

(Відповідь: a) ; б) ; в) 226/3.)

2.23. A(-6,-3,-5,), B (5,1,7), C(3,5,-1), D(4,-2,9); a)ACD; б)L=BC, A і D.

(Відповідь: a) ; б) ; в) 4/3.)

2.24. A(7,4,2,), B (-5,3,-9), C(1,-5,3), D(7,-9,1); a)ABD; б)L=BD, A і C.

(Відповідь: a) ; б) ; в) 186.)

2.25. A(-8,2,7,), B (3,-5,9), C(2,4,-6), D(4,6,-5); a)ACD; б)L=AD, B і C.

(Відповідь: a) ; б) ; в) 296/3.)

2.26. A(4,3,1,), B (2,7,5), C(-4,-2,4), D(2,-3,-5); a)ACD; б)L=AB, C і D.

(Відповідь: a) ; б) ; в) 80/3.)

2.27. A(-9,-7,4,), B (-4,3,-1), C(5,-4,2), D(3,4,4); a)ACD; б)L=CD, A і B.

(Відповідь: a) ; б) ; в) 120.)

2.28. A(3,5,3,), B (-3,2,8), C(-3,-2,6), D(7,8,-2); a)ACD; б)L=BD, A і C.

(Відповідь: a) ; б) ; в) 26/3.)

2.29. A(4,2,3,), B (-5,-4,2), C(5,7,-4), D(6,4,-7); a)ABD; б)L=AD, B і C.

(Відповідь: a) ; б) ; в) 178/3.)

2.30. A(-4,-2,-3,), B (2,5,7), C(6,3,-1), D(6,-4,1); a)ACD; б)L=BC, A і D.

(Відповідь: a) ; б) ; в) 116.)

3. Сила F прикладена до крапки А.

Знайти : а) роботу сили F в випадку , коли крапка її прикладення , рухаясь прямолінійно , переміщується в крапку B;

б) модуль моменту сили F відносно крапки В.

3.1. F= (5,-3,9), A(3,4,-6), B(2,6,5).

(Відповідь: a)88; б) ;.)

3.2. F= (-3,1,-9), A(6,-3,5), B(9,5,-7). (Відповідь: a)107; б) ;.)

3.3. F= (2,19,-4), A(5, 3,4), B(6,-4,-1). (Відповідь: a)111; б) ;.)

3.4. F= (-4,5,-7), A(4,-2,3), B(7,0,-3). (Відповідь: a)40; б) ;.)

3.5. F= (4,11,-6), A(3,5,1), B(4,-2,-3). (Відповідь: a)49; б) ;.)

3.6. F= (3,-5,7), A(2,3,-5), B(0,1,3). (Відповідь: a)45; б) ;.)

3.7. F= (5,4,11), A(6,1,-5), B(4,2,-6). (Відповідь: a)17; б) ;.)

3.8. F= (-9,5,7), A(1,6,-3), B(4,-3,5). (Відповідь: a)16; б) ;.)

3.9. F= (6,5,-7), A(7,-6,4), B(4,9,6). (Відповідь: a)127; б) ;.)

3.10. F= (-5,4,4), A(3,7,-5), B(2,-4,1). (Відповідь: a)15; б) ;.)

3.11. F= (4,7,-3), A(5,-4,2), B(8,5,-4). (Відповідь: a)93; б) ;.)

3.12. F= (2,2,9), A(4,2,-3), B(2,4,0). (Відповідь: a)27; б) 28;.)

Дано три сили P, Q, R, прикладені до крапки А.

Знайти : а) роботу, виробляєму рівнодіючій цих сил , коли крапка її прикладення , рухаясь прямолінійно , переміщається в крапку В;

б) величіну моменту рівнодіючих цих сил відносно крапки В.

3.13. P=(9,-3,4 ), Q=(5,6,-2), R=(-4,-2,7), A(-5,4,-2), B(4,6,-5).

(Відповідь: a)65; б) .)

3.14. P=(5,-2,3 ), Q=(4,5,-3), R=(-1,-3,6), A(7,1,-5), B(2,-3,-6).

(Відповідь: a)46; б) .)

3.15. P=(3,-5,4 ), Q=(5,6,-3), R=(-7,-1,8), A(-3,5,9), B(5,6,-3).

(Відповідь: a)100; б) .)

3.16. P=(-10,6,5 ), Q=(4,-9,7), R=(5,3,-3), A(4,-5,9), B(4,7,-5).

(Відповідь: a)126; б) .)

3.17. P=(5,-3,1 ), Q=(4,2,-6), R=(-5,-3,7), A(-5,3,7), B(3,8,-5).

(Відповідь: a)4; б) .)

3.18. P=(-5,8,4 ), Q=(6,-7,3), R=(3,1,-5), A(2,-4,7), B(0,7,4).

(Відповідь: a)8; б) .)

3.19. P=(7,-5,2 ), Q=(3,4,-8), R=(-2,-4,3), A(-3,2,0), B(6,4,-3).

(Відповідь: a)71; б) .)

3.20. P=(3,-4,2 ), Q=(2,3,-5), R=(-3,-2,4), A(5,3,-7), B(4,-1,-4).

(Відповідь: a)13; б) .)

3.21. P=(4,-2,-5 ), Q=(5,1,-3), R=(-6, 2,5), A(-3,2,-6), B(4,5,-3).

(Відповідь: a)15; б) .)

3.22. P=(7,3,-4 ), Q=(9,-4,2), R=(-6,1,4), A(-7,2,5), B(4,-2,11).

(Відповідь: a)122; б) .)

3.23. P=(9,-4,4 ), Q=(-4,6,-3), R=(3,4,2), A(5,-4,3), B(4,-5,9).

(Відповідь: a)4; б) .)

3.24. P=(6,-4,5 ), Q=(-5,7,8), R=(5,1,-3), A(-5,-4,2), B(7,-3,6).

(Відповідь: a)128; б) .)

3.25. P=(5,5,-6 ), Q=(7,-6,6), R=(-4,3,4), A(-9,4,7), B(8,-1,7).

(Відповідь: a)126; б) .)

3.26. P=(7,-6,2 ), Q=(-6,2,-1), R=(1,6,4), A(3,-6,1), B(6,-2,7).

(Відповідь: a)44; б) .)

3.27. P=(4,-2,3 ), Q=(-2,5,6), R=(7,3,-1), A(-3,-2,-5), B(9,-5,4).

(Відповідь: a)82; б) .)

3.28. P=(7,3,-4 ), Q=(3,-2,2), R=(-5,4,3), A(-5,0,4), B(4,-3,5).

(Відповідь: a)31; б) .)

3.29. P=(3,-2,4 ), Q=(-4,4,-3), R=(3,4,2), A(1,-4,3), B(4,0,-2).

(Відповідь: a)15; б) .)

3.30. P=(2,-1,-3 ), Q=(3,2,-1), R=(-4,1,3), A(-1,4,-2), B(2,3,-1).

(Відповідь: a)0; б) .)

ПРАКТИЧНА РОБОТА №5

ТЕМА: Пряма у просторі. Площина.

МЕТА: Навчитися складати рівняння прямої, площини.

Рішення типового варіанту.

1) Дано чотири точки А₁(4,7,8), А₂( 1,13,0), А₃(2,4,9), А₄(l,8,9).Скласти рівняння:

а) площини А₂а₃;

б) прямої А₄М, перпендикулярної до площини А₁А₂А₃;

г) прямої А₄N , паралельної прямій А₁ А₂.

Обчислити :

д) синус кута між прямою А₁А₄ та площиною А₁А₂А₃;

е) косинус кута між координатною площиною Оху та площиною А₁А₂А₃.

* а)Використовуючи формулу (3.4), складаємо рівняння площини А₁А₂А₃:

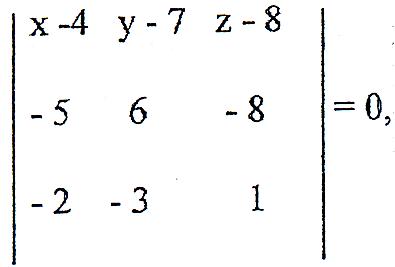
звідки 6х - 7у - 9z+97=0;

б) Враховуючи рівняння прямої, що проходить через дві точки , рівняння прямої А₁А₂ можна записати у вигляді

(x - 4)/5=(y-7)/-6=(z-8)/8;

в)З умови перпендикулярності прямої А₄М та площини А₁А₂A₃ витікає, що і якості направляючого вектора прямої s можна взяти нормальний вектор n=7,- 9) площини А₁А₂А_З, Тоді рівняння прямої А₄М з урахунком рівнянь запишеться у вигляді

(х - 1)/6=(у - 8)/- 7= (z-9)/- 9;

г)Ţак як пряма А₄N паралельна прямій А₁ А₂, то іх направляючі вектори s₁ і s₂ можна вважати співпадаючими: s_l=s₂=(5, - 6,8) Значитъ, рівняння прямої має вигляд

(х- l)/5=(y-8)/-6=(z-9)/8;

д)За формулою

sin φ= =

що приблизно дорівнює 0,8;

е)Вīдповiдно до формули (3.5)

cos φ = = = = -0.7

2. Скласти рівняння площини, що проходить через точки М(4,3,1) і N( -2,0,-1) паралельно прямій проведеній через точки А(1,1,-1) і

В(- 3,1,0).

• Відповідно формулi (З.9), рiвняння прямої АВ має вигляд

(x-l)/-4=(y-1)/0=(z+l)/1

Якщо площина проходить через точку М(4,3,1), то іі рівняння можна записати у вигляді А(х-4)+В(у­3)+С(z­l)=3.

Так як ця площина проходить і через, точку N(- 2,0,-1), то виконується умова ;

А( -2,- 4)+В(0,- 3)+С (-1,-1)=0 або

6А+3В+2С=0

Так як шукана площина паралельна найденій прямій АВ, то з урахуванням умови паралельності (3.16) маємо:

-4А+ОВ+1С=0 або 4 А- С=0.

Рішаючи систему

Знаходимо що С=4А, В= - 14/3

А підставивши отримані значення С та В у рівняння шуканої площини, отримуємо:

А(х - 4) -14/3A(y-3)+4А(z-1)=0.

Так як А не дорівнює нулю, то отримане рівняння еквівалентне рівнянню

3(x-4)-14(y-3)+12(z-l)=0.

3.Знайти координати x2, y2, z2 точки M₂ симетричної точці

M₁ (6,- 4,2) відносно площини:

x=6+t, y= -4+t, z= - 2+t.

Рішивши ix сумісно з рівнянням даної площини , знайдемо t=l і, відповідно ,точку М перетину прямої М₁М₂ з даною площиною : М(7,- 3,- 1).

Так як точка М являється серединою відрізку М₁М₂, то дійсні рівняння :

7=(6+х2)/2, - 3=( -4+у2)/2 , -1=(­2+z2)/2 ,

з яких знаходимо координати точки M2: x2=8, y2=2, z2=0.

1Дані чотири точки А1 (х1 ,у1 ),А2 (х2 ,у2 ),АЗ (х3 ,у 3) та

А4 (х4 ,у 4).

Скласти рівняння:

а)площини А1,А2,АЗ;

б)прямоï А1,А2; в)прямоï А4М, перпендикулярної до площини А1,А2,АЗ;

г)прямої АЗN,паралельноi до прямої А1А2;

д) площині, що проходить через точку А4 перпедикулярну до прямої А1,А2.

Обчислити:

е) синус кута між прямою А1 А4 та площиною A1А2АЗ;

ж) косинус кута між координатною площиною Оху та площиною А1А2АЗ.

1. А1(З,1,4), А2(-l,6,l), А3(-1,1,6), А4(0,4,-1).

2. A1(3,-1,2), А2(-1,0,1), А3(1,7,З), А4(8,5,8).

3. А1(З,5,4), А2(5,8,З), А3(1,2,-2), A4(-1,0,2).

4. А1(2,4,З), А2(1,1,5), А3(4,9,З), А4(З,6,7).

5. А1(9,5,5), А2(-З,7,1), А3(5,7,8), А4(6,9,2).

6. А1 (0,7,1), А2(2,-1,5), А3(1,6,З), А4(З,9,8).

7. А1(5,5,4), А2(1,-1,4), А3(3,5,1), А4(5,8,-1).

8. А1(6,1,1), А2(4,6,6), А3(4,2,0), А4(1,2,6).

9. А1 (7,5,3), А2(9,4,4), А3(4,5,7), А4(7,9,6).

10.А1(6,8,2), А2(5,4,7), А3(2,4,7), А4(7,З,7).

11.А1(4,2,5), А2(0,7,1), А3(0,2,7), А4(1,5,0).

12.A1 (4,4 10), А2(7,10,2), A3(2,8,4), A4(9,6,9).

13.А1(4,6,5), А2(6,9,4), А3(2,10,10), А4(7,5,9).

14.A1(3,5,4), A2(8,7,4), A3(5,10,4), A4(4,7,8).

15.А1(10,9,6), А2(2,8,2), А3(9,8,9), А4(7,10,3).

16.А1(1,8,2), А2(5,2,6), А3(5,7,4), А4(4,10,9).

17.А1(6,6,5), А2(4,9,5), А3(4,6,11), А4(6,9,З).

18.A1(7,2,2), A2(-5,7,-7), A3(5,-З,1), A4(2,3,7).

19.A1(8-6,4), A2(10,5,-5), A3(5,6,-8), A4(8,10,7).

20.А1(1,-1,3), А2(6,5,8), А3(3,5,8), А4(8,4,1).

21.А1(1,-2,7), А2(4,2,10), А3(2,3,5), А4(5,3,7).

22.А1(4,2,10), А2(1,2,0), A3(3,5,7), A4(2,-3,5).

23.A1(2,1,5), A2(5,3,-7), A3(1,2,7), A4(4,2,0).

24.А1 (5,3,7), А2(-2,З,5), А3(4,2,10), А4(1,2,7).

25.А1(4,З,5), А2(1,9,7), А3(0,2,0), А4(5,З,10).

26.A1(3,2,5), A2(4,0,6), A3(2,6,5), A4(6,4,-1).

27.A1(2,1,6), A2(1,4,9), A3(2,-5,8) A4(5,4,2).

28.А1(2,1,7),А2(3,3,6),А3(2,-З,9),А4(1,2,5).

29.A1(2,-1,7), A2(6,3,1) A3(3,2,8),A4(2,-3,7).

30.A1(0,4,5), A2(3,-2,1), A3(4,5,6), A4(3,3,2).

2. Pішити наступні задачі.

1. Знайти величину відрізку, відсікаємих на осях координат площиною, що проходить через точку М(-2,7,3) паралельно площині х- 4y+5z-i=0.

(Відповідь:-1/15, 4/15, -1/3) .

2. Скласти рівняння площини, що проходить через середину відрізку М₁М₂ перпендикулярно до цього відрізку, якщо М₁(1,5,б), M2(-1,7,10).

(Відповідь : x-y-2z+22=0).

3.Знайти відстань від точки M(2;0;-0.5) до площини 4х-4у+2z+17=0.

(Відповідь : d=4)

4.Скласти рівняння площини, що проходить через точку A(2,-3,5) паралельно площині Оху .

(Відповідь: z-5=0).

5. Скласти рівняння площини, що проходить через вісь Ох та точку А(2,5,-l).

(Відповідь: у+5z=0).

6.Скласти рівняння площини б, що проходить через точки А(2,5,-1), B(֊3,l,3) паралельно осі Оу.

(Відповідь: 4х+5zЗ=0).

7. Скласти рівняння площини, що проходить через т.А(3,4,0) і пряму (x-2)/l=(y-3)/2=(z+1)/2.

(Відповідь: уz-4=0).

8.Скласти рівняння площини, що проходить через дві паралельні прямі (x-3)/2=y/l=(z-l)/2 та (х+1)/2=(у-1)/1= z/2.

(Відповідь: х+2у-2z-1=0).

9.Скласти загальні рівняння прямої, утвореної перетином площини

3х-у-7z+9=0 з площиною , що проходить через вісь Ох та точку A(3,2,-5).

(Відповідь: 3x-y-7z+9=0,5y+2z=0).

10.Скласти рівняння площини в "відрізках", якщо вона походить через точку М

10,1) та відсікає на осі Ох відрізок а=-3, а на осі Оz — відрізок с=2.

(Відповідь: Х;3+y/-4+z/2=l).

11.Скласти рівняння площини, що проходить через точку А(2,З,- 4) паралельно двом векторам

а= (4,1,- 1) та b=(2,- Լ2).

(Відповідь: x-10y-6z+4=0).

12.Скласти рівняння площини, що проходить через точки А(1,1,0), B(2,- 1,- 1) перпендикулярно до площини 5х+2у-3z-7=0.

(Відповідь: х+2у3z-3=0).

13.Скласти рівняння площини, що проходить через початок координат перпендикулярно до двох площин 2х3у+z-1=0 і х-у+5z+3=0.

(Відповідь: 14x+9y-z=0).

14.Скласти рівняння площини, що проходить через точки А(3,- 1,2), В(2,l,4) паралельно вектору а=(5,- 2,- l).

(Відповідь: 2x+9y-8z+19=0).

15.Скласти рівняння площини , що проходить через початок координат ׃ перпендикулярно до вектору , якщо А(5,- 2,3), В(1,- 3,5).

(Відповідь: 4x+y-2z=0).

16. Найти величини відрізків, що відсікаються на вісях координат площиною , л проходить через точку М(2,- 3,3) паралельно площині 3х+ у-3z=0.

(Відповідь: -2,-6,2).

17.Скласти рівняння площини ,що проходить через точку М(l,- l,2),якщо М_l(

4), М2(-1,2,- З).(Вıдповідь: 3х+у-z=0). (перпендикулярно до відрізку М₁М₂ 18.Показати , що пряма х/6=(у-З)/8=(z - l)/-9 паралельна площині x+3y-2z-l=0,a пряма x=t+7, у=t -2, z=2t+1 лежить в цій площині.

19-Скласти загальне рівняння площини, що проходить через точку

А(3,- 4,1) паралельно координатній площині Охz.(Вíдп: y+4=0).

20.Скласти рівняння площини , що проходить через вісь Оу та точку М(З,-5,2).(Вıдповідь:2х-3z=0).

21.Скласти рівняння площини , що проходить через точки М(l,2,3) і

N(- 3,4,- 5) паралельно вісі Оz.

(Вiдповідь: х+2у - 5=0).

22. Скласти рівняння площини ,що проходить через точку М(2,З,- ]) та пряму х 3,у=2t+5,z=-Зt+l.

(Вiдпрвідь: l0х+13у+12z ­ 47=0).

23.Знайти проекцію точки М(4, -3,1) еа площину х - 2у - z - 15=0.

(Відповідь:М₁(5, -5,0)

24.Визначити, при якому значенні В площини х - 4y-z - 1=0 і

2x+By+10z - 3=0 будуть перпендикулярнi.

(Вiдповідь: В=З).

25.Скласти рівняння площини, що проходить через точкуМ(2, -3,-4) та відсікає вісях координат відмінні від нуля відрізки однакової величини. (Відповідь: x+y+z+5=0).

2б.Пpи яких значеннях n та А пряма х/3=(у - 5)/n=(z+5)/6 перпедикулярна

до площини Ах+2у - 2z - 7=0 ? (Відповідь: А= - l,n= - 6).

27.Скласти рівняння площини, що проходить через точки A(2,3, - 1),

В(l,l,4) перпендикулярно до площини х - 4y+3z+2=0.

(Відп: 7x+4y+3z - 23=0).

28,Скласти рівняння площини ,що проходить через початок координат

Перпендикулярно до плоскостей х+5у - z+7=0 і Зх - у+2z - 3=0.

(Відп: 9х-5у - 16z=0).

29,Скласти рівняння площини ,що проходить через точки М(2,З, 5) і

N( -1,1, -6) паралельно вектору а=(4,4,З).(Вiдп: 2х - 5y+4z+31=0).

30,Визначити, при якому значенні С площини Зх - 5у+Сz - 3=0 і

x - 3y+2z+5=0 будуть перпендикулярні.(Відп: С= -9).