11.Доказать формулы вычисления моментов инерции круга и однородного круглого цилиндра.

К РУГ

Вычислим момент инерции круга радиусом R и массой М относительно его центра О. Разобьем круг концентрическими окружностями на элементарные плоские кольца. Радиус такого кольца обозначим через , его бесконечно малую ширину через , а массу . Элементарное кольцо - материальную окружность, найдём ее момент инерции. Разобьем, всю окружность на бесконечно малые элементы - дуги. Массу элемента обозначим через . Все элементы находятся от точки О на одном расстоянии . Поэтому момент инерции такого кольца равен: . Поверхностная плотность однородного круга: (кг/м²).

Масса элементарного кольца: . Момент инерции круга равен: . Предел этой суммы - определённый интеграл по переменной r в пределах от 0 до R: .

Моменты инерции круга относительно осей Ох и Oy: воспользуемся формулой, связывающей осевые моменты инерции с полярным, и учтём что осевые моменты инерции круга в силу симметрии равны между собой. Получаем: .

КРУГЛЫЙ ЦИЛИНДР

Вычислим момент инерции круглого цилиндра относительно его оси вращения z. Радиус основания цилиндра R, а его масса - M. Разобьем цилиндр плоскостями, параллельными его основанию, на бесконечно тонкие круглые пластики, масса которых . Момент инерции такой пластинки относительно оси вращения цилиндра: .

Момент инерции цилиндра: .

12.Доказать теорему о зависимости между моментами инерции относительно параллельных осей (теорему Гюйгенса–Штейнера).

М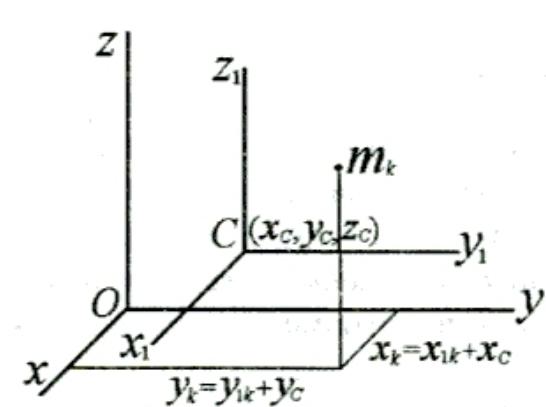 еханическая система N материальных точек, массы которых (k = 1, 2, ..., N). Положение точек определено по отношению к системе координат Oxyz. Координаты центра масс x_С,y_С,z_С. Свяжем с центром масс систему осей Сx₁y₁z₁, параллельных осям xyz. Известен момент инерции системы относительно оси Сz₁, проходящей через центр масс.

Моменты инерции относит. осей Сz₁ и Оz будут равны: , . Координаты в системах связны: , (1). Подставим (1), в выражение :

, так как ось Сz₁ проходит через центр масс, - масса системы, - расстояние между осями Сz₁ и Оz.

13.Дать определение количества движения точки и механической системы. Доказать формулу для вычисления количества движения механической системы. Что такое элементарный и полный импульс силы.

- Количеством движения материальной точки называется векторная величина, равная произведению массы точки на ее скорость: .

- Количеством движения механической системы состоящей из N материальных точек, называется векторная величина, равная геометрической сумме количеств движения точек, входящих в механическую систему или произведению массы всей системы на скорость центра масс: .

- Из определения радиус-вектора центра масс: . Дифференцируем обе части по t: , - вектор скорости центра масс.

- Элементарным импульсом силы характеризуют действие переменной силы на материальную точку в течении времени dt. . Полным импульсом силы , действующей на материальную точку в течение времени t, называется вектор: .