9.Дать определение моментов инерции. Доказать связь между полярным и осевыми моментами инерции. Что такое радиус инерции. Какая ось называется главной центральной осью тела.
- Полярным моментом
инерции
материальной точки М называется
произведение массы m этой точки на
квадрат расстояния r до точки О (полюса):
.
- Осевым моментом
инерции материальной точки М относительно
оси Оl называется произведение массы
точки m на квадрат расстояние h до оси
Оl:
.
- Моменты инерции
материальной точки относительно
декартовых осей:
.
Перепишем:
(1). Момент инерции точки относительно
начала координат равен:
,
перепишем:
(2).
Сложим, левые и
правые части (1):
.
С учётом (2):
.
- Точка находиться
в плоскости xOy, моменты инерции материальной
точки относительно осей х и y равны:
.
Перепишем:
(3). Момент инерции точки относительно
начала координат равен:
,
перепишем:
(4). Сложим, левые и правые части (3):
.
С учётом (4):
.
- Момент инерции
тела относительно оси Оl:
.
- радиус инерции тела относительно
данной оси:
.
Радиус инерции - расстояние от оси до
точки, в которой нужно сосредоточить
всю m
тела, чтобы момент инерции массы был
равен моменту инерции тела относительно
данной оси.
- Если оба центробежных
момента инерции, содерж. в индексах
значок некоторой коорд. оси равны нулю,
то эта ось - главная осью инерции тела.
Например:
,
то z - главная ось инерции. Если эта ось
проходит через центр масс тела, то она
называется главной центральной осью
инерции.
10.Доказать формулы для вычисления моментов инерции прямолинейного тонкого стержня и прямоугольной пластины.
СТЕРЖЕНЬ
С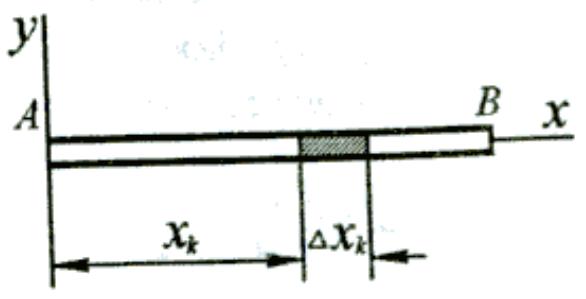
тержень
массой М - материальный прямолинейный
отрезок АВ длиной l. Вычислим момент
инерции этого стержня относительно оси
Аy
АВ.
Разобьем стержень на бесконечно малые
отрезки
.
Расстояние от
до точки А обозначим
,
а его массу -
.
Тогда:
.
Линейная плотность
стержня:
(кг/м). Масса
элементарного отрезка
равна:
.
Стержень однородный, тогда:
.
Предел этой суммы - определённый интеграл
по х в пределах от 0 до l:
.
Момент инерции
стержня относительно центра масс С
вычисляется аналогично. Пределы в этом
случае надо брать от
.
В результате:
.
ПРЯМОУГОЛЬНИК
Т
онкая
однородная пластина ОАВС со сторонами
а и b и массой М. Вычислим момент инерции
относительно оси y (стороны ОА). Разобьем
площадь ОАВС прямыми, параллельными
оси х, на бесконечно узкие полоски. Масса
полоски -
.
Каждая полоска является прямолинейным
отрезком, момент инерции которого:
.
Момент инерции
всего прямоугольника:
.
Аналогично
относительно оси х:
.
Для момента инерции ОАВС относительно
вершины О на основании связи полярного
и осевых моментов, имеем:
.