45.Докажите условия равновесия механической системы в обобщенных координатах.

На систему из N материальных точек наложены связи, удовл. принципу возможных перемещений. Запишем: (1). Система имеет n степеней свободы => ее положение опред. n обобщ. координатами , а радиус-вектор , k-ой точки: . Возможное перемещ. каждой точки: (2). Подставим (2) в (1): , отсюда получим: (3). Вариации обобщ. координат независимы друг от друга => (3) выполнится, когда все обобщенные силы равны нулю. Условие равновесия голономной системы в обобщ. коорд.: .

46.Изложите вывод принципа Даламбера–Лагранжа (общего уравнения динамики), сформулируйте его и запишите соответствующие формулы в векторной и аналитической формах.

На голономную систему наложены удерживающие и идеальные связи. Применим к системе принцип Даламбера. Такая система сил, будет удовлетворять условию: , (1).

Зафиксируем время и сообщим точкам возможные перемещ. . Умножим (1) скалярно на и просуммируем по k: . в силу идеальности связей. ; , и окончательно:

При любом движении механической системы с идеальными и удерживающими связями в каждый данный момент сумма возможных работ всех активных сил и сил инерции на любом возможном перемещении равна нулю.

В проекциях на декартовы оси координат:

47.Запишите уравнения Лагранжа II рода. Изложите последовательность действий при решении задач аналитической динамики с помощью уравнений Лагранжа II рода.

, ( )

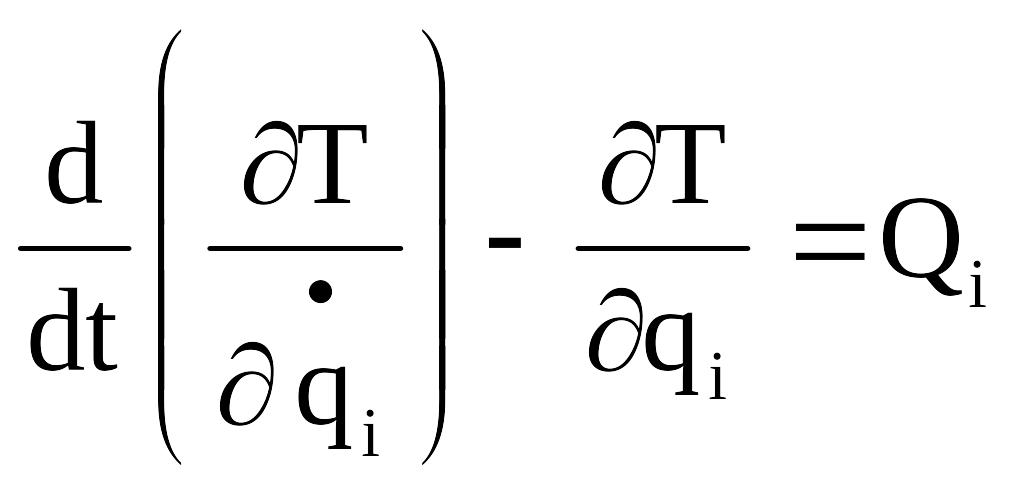3N - число координат у N точек системы в пространстве.

s - количество связей, нахоженных на систему.

n=3N-s - число обобщ. координат определяющих положение системы (если связи голономные и удерживающие, то n - количество степеней свободы системы).

1) определить число степеней свободы механической системы и выбрать удобные обобщ. координаты;

2) вычислить Т системы в ее абсолютном движении и выразить эту энергию через обобщ. координаты и обобщ. скорости;

3) изобразить действующие на систему активные силы и силы трения, составить выражения для работы этих сил на возможном перемещ. и из этого выражения определить обобщ. силы соотв. выбранным обобщ. координатам;

4) вычислить производные, входящие в уравнения Лагранжа;

5) подставить все вычисленные величины в уравнения Лагранжа;

6) найти решения получившихся ДУ, соотв. заданным начальным условиям.

48.Изложите вывод уравнений Лагранжа II рода в случае потенциального поля сил. Что такое функция Лагранжа.

Если силы пот.: ( ), ур-я Лагранжа примут вид: ( ). Пот. энергия не зависит от обобщ. скоростей и явл. ф-цией только обобщ. координат => ур-я Лагранжа примут вид: ( ).

Ф-ция, равная разности кин. и пот. энергий механической системы, наз. ф-цией Лагранжа, или кинетическим потенциалом: ( ) => ( ).

49.Основы теории малых колебаний около положения устойчивого равновесия. Сформулировать теорему Лагранжа–Дирихле.

- Механическая система может совершать малые колебания только около положения устойчивого равновесия.

- Положение системы называется положением равновесия, если в начальный момент времени система была приведена в это положение при нулевых скоростях и всё время остаётся в этом положении.

- Положение равновесия системы бывает: устойчивым, неустойчивым, безразличным.

- Под устойчивостью мех. сист. подразумевается такое ее свойство, когда все величины, определяющие ее состояние, при малых возмущениях остаются вблизи тех их значений, которые характеризуют невозмущенное состояние системы.

Л-Д: Если в некотором положении консервативной механической системы потенциальная энергия имеет строгий минимум, то это положение является положением устойчивого равновесия системы.