Основные правила дифференцируемости

1) производная постоянной величины = 0 с-const (с)`=0

2) производная от переменной по этой же переменной =1 x_x`=1

3) производная суммы (разности) равна сумме (разности) производных этих функций y`=u`(x)+v`(x)-w`(x)=(u(x)+v(x)+w(x))`

4) производная произведения равна (u(x)v(x))`=u`(x)v(x)+u(x)v`(x)

5) постоянный множитель можно выносить за знак произведения (cu(x))`=cu`(x)

6) производная дроби равна ( )`=

Производная сложной функции

7) сложная функция равна y=f(u), где u=φ(x) → y_x`=y<sub>u</sub>` u_x`

Производная обратной функции

8) обратная функция y=f(x)(прямая) x=φ(y) (обратная) y_x`=1/x<sub>y</sub>` x_y`=1/y<sub>x</sub>`

Производная основных элементарных функций

y=sinu y`=cosuu`

y=cosu y`=-sinuu`

y=tgu y`= u`

y=ctgu y`=- u`

y=arcsinu y`= u`

y=arccosu y`=- u`

y=arctgu y`= u`

y=arcctgu y`=- u`

y=log_au y`= u`

y=lnu y`= u`

y=a^u y`=a<sup>u</sup>lnau`

y=e^u y`=e<sup>u</sup>u`

y=u^a y`=au<sup>a-1</sup>u`

y=u(x)^v(x) y`=u<sup>v</sup>lnuv`+vu^v-1u`

Гиперболические функции и их дифференцирование

chx=

shx=

thx=

cthx=

(chx)`=shx

(shx)`=chx

ch²x-sh²x=1

(thx)`=

(cthx)`=

Дифференцирование функции заданной неявно

x²+y²-R²=0 дифференцируем относительно у

2x+2yy`-0=0

y`=-

Дифференцирование функции заданной параметрически

y`(x)=

Дифференциал функции. Его связь с производной

Дифференциал функции в точке х называется главная чать ее приращения, равная произведению производной функции на приращение аргумента и обозначается dy

dy=y`(x)dx (когда х независимая переменная) или dy=y`(x) x

y`(x)=

Применение дифференциала в приближенных вычислениях

f(x+ x)≈f(x)+dy

Геометрический смысл дифференциала

Приращение ординаты касательной проведенной к данной кривой в точке М при переходе точки М с абсциссой х в точку N с абсциссой x+∆x по кривой

АВ=dy=y`(x)dx

Основные правила и формулы нахождения дифференциала

Dc=0, c`=0

D(cu(x))=cdu

D(u+v)=du+dv

D(uv)=vdu+udv

D(u/v)=

Инвариантность формы дифференциала первого порядка

Форма дифференциала первого порядка сохраняется вне зависимости от того, является ли аргумент независимым или является в свою очередь функцией другого аргумента.

Дана сложная функция y=f(u), u=φ(x)

Dy=y`(x)dx=f`(u)du

Производные и дифференциалы высших порядков

Производные:

Функция задана параметрически

y`_x=

y``=

Дифференциалы:

f`(x)=

f``(x)=

d²y=f`(x)dx²

Теорема Ролля. Геометрический смысл теоремы Ролля.

Если функция f(x) непрерывна на отрезке [a,b] и дифференцируема на интервале (a,b) и на концах отрезка принимает одинаковые значения, то найдется хотя бы одна точка c∈(a;b), в которой производная f`(x) обращается в ноль f`(c)=0

Геометрический смысл означает что на графике функции f(x) найдется точка, в которой касательная к графику параллельна оси Ох

Теорема Лагранжа. Геометрический смысл теоремы Лагранжа

Если функция f(x) непрерывна на отрезке [a,b] и дифференцируема на интервале (a,b), то найдется хотя бы одна точка c∈(a;b) такая, что выполняется равенство f(b)-f(a)=f`(c)(b-a)

Геометрический смысл означает, что на графике функции f(x) найдется точка с, в которой касательная к графику параллельна секущей АВ

Теорема Коши

Если функции f(x) и φ(x) непрерывны на отрезке [a,b] и дифференцируемsна интервале (a,b) ,причем φ`(x)≠0 для x∈(a;b) , то найдется хотя бы одна точка c∈(a;b) такая, что выполняется неравенство:

Правило Лопиталя и его применение к вычислению пределов

Если  , и если функции f(x) и g(x) – дифференцируемы в окрестности точки  , то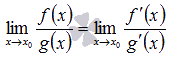 

Возрастание и убывание функции. Необходимый и достаточный признаки возрастания и убывания функции

Необходимое условие:

Если дифференцируемая на интервале (a,b) функция f(x) возрастает (убывает), то f`(x)≥0 (f`(x)≤0), для любых х принадлежащим интервалу

Достаточные условия:

Если функция f(x) дифференцируема на интервале (a,b) и f`(x)>0 (f`(x)<0) для любых х принадлежащим интервалу, то это функция возрастает (убывает) на интервале (a,b)

Экстремум функций одной переменной. Точки экстремума. Необходимый признак существования экстремума

Точка х₀ называется точкой максимума функции f(x) если существует такая окрестность точки х₀, что для всех х≠х₀ из этой окрестности выполняется условие f(x)<f(x₀)

Аналогично и для точки минимума, только f(x)>f(x₀)

Если дифференцируемая функция y=f(x) имеет экстремум в точке х₀, то ее производная в это точке равна нулю f`(x₀)=0

Достаточные признаки существования экстремума

Если непрерывная функция f(x) дифференцируема в некоторой окрестности критической точки х₀ и при переходе через нее (слева напрво) производная f`(x) меняет знак с плюса на минус, то х₀ есть точка максимума, с плюса на минус, то х₀ – точка минимума

Если в точке х₀ первая производная функции f(x) , равна нулю (f`(x₀)=0), а вторая производная в точке х₀ существует и отлична от нуля (f``(x<sub>0</sub>)≠0), то при f``(x₀)<0 в точке х₀, функция имеет максимум и минимум при f``(x₀)>0