Непрерывность функции в точке. Определение. Свойства функций, непрерывных в точке

Функция определенная в окрестности называется непрерывная в х₀ если существует предел функции при х→х₀ и этот предел равен значению функции в точке х₀

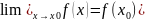
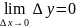(эквивалентная к предыдущей)

Св-ва:

1) Сумма произведение и частное двух непрерывных функций есть функция непрерывная

2) Основные элементы функции непрерывны в области своего определения

3) y=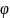 (x) непрерывна в х₀, а f(y) непрерывна в y₀, y₀= (x₀) тогда сложная функция f( (x)) непрерывна в точке х₀

Непрерывность функции на отрезке

Функция y=f(x) называется непрерывной на отрезке [a,b] , если она непрерывна в интервале (a,b) и в точке х=а непрерывна справа, а в точке x=b непрерывна слева

Свойства функций, непрерывных на отрезке

Вейерштрассе: Если функция непрерывна на отрезке, то она достигает на нем свои наибольшие и наименьшие значения

Если функция y=f(x)  непрерывна на отрезке, то она ограничена на этом отрезке

Если функция y=f(x)  непрерывна на отрезке [a,b] и принимает на его концах неравные значения f(a)=A и f(b)=B, то на этом отрезке она принимает и все промежуточные значения между A и B

Если функция y=f(x)  непрерывна на отрезке [a,b] и на его концах принимает значения разных знаков, то внутри отрезка найдется одна такая точка с, в которой функция f(x) обращается в ноль

Если функция y=f(x)  непрерывна на отрезке [a,b] и строго возрастает, то для нее существует также строго возрастающая обратная функция, которая будет непрерывна на отрезке [А,В] где А=f(a), B=f(b)

Точки разрыва – точки в которых нарушается непрерывность

Точка разрыва первого рода – это точка в которой существуют конечные односторонние пределы

Точка разрыва второго рода – это точка где хотя бы один из односторонних пределов не существует или равен бесконечности \

Производная. Определение. Механический и геометрический смысл производной

Производной f(x) по аргументу х называют предел отношения приращения функции к приращению аргумента, когда последний стремится к нулю

Если функция описывает какой то физический процесс, то производная есть скорость протекания этого процесса, это и есть механический смысл производной

Производная f `(x) в точке х равна угловому коэффициенту касательной к графику функции y=f(x) в точке, абсцисса которой равна х, в этом и заключается геометрический смысл производной

Уравнение касательной y-y₀=f `(x₀)(x-x₀)

Дифференцируемость функции. Определение. Теорема о непрерывности дифференцируемой функции

Функция f называется дифференцируемой в точке х=х₀ если она имеет там производную

Функция f дифференцируема на промежутке если она дифференцируема в каждой точке данного интервала

Если функция f дифференцируема в некоторой точке х=х₀, то она и непрерывна в этой точке

Обратное утверждение теоремы неверно!