Гипербола. Определение. Вывод канонического уравнения. Исследование формы гиперболы

Гипербола – множество точек в плоскости, модуль разности расстояний от которых до двух данных точек называемых фокусами есть величина постоянная = 2а

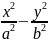= 1

Т.к. х и у в уравнении в квадрате, значит гипербола будет симметрична относительно Ох и Оу

Точки пересечения гиперболы с осями называются вершинами гиперболы, с осью Оу гипербола пересечений не имеет

Вывести у

Парабола. Определение. Вывод канонического уравнения

Парабола – это множество точек, расстояние которых до некоторых точек называемых фокусами и до некоторой прямой называемой директрисой равно.

y² = 2 p x

Парабола проходит через начало координат

Парабола симметрична оси Ох

Если р>0, то ветви параболы направлены вправо

Исследование общего уравнения линии второго порядка в случае отсутствия члена с произведением текущих координат

Ax²+2Bxy+Cy²+2Dx+2Ey+N=0

A,B,C≠0

Сфера. Определение. Вывод канонического уравнения.

Сфера – это множество точек стоящих от центра на одно и то же расстояние r

r²= (x-a)²+(y-b)²+(z-c)²

Цилиндрические поверхности

Поверхность образованная движением образующей (L), которая перемещается в пространстве, сохраняя при это направление и каждый раз пересекая направляющую (K) называется цилиндрической поверхностью или цилиндр

Название цилиндра определяется названием образующей: Эллиптическая (по эллипсу, уравнение эллипса), Круговая…

Эллипсоиды

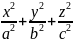=1

Гиперболоид

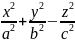= 1

Параболоид

x²+y²=2px

Конические поверхности

Поверхность, образуемая движением линии АВ , перемещающуюся в пространстве так, что она постоянно проходит через вершину и пересекает направляющую

Функция. Основные понятия. Способы ее задания

Функция- соответствие f, которое каждому элементу x сопоставляет только один у

Множество Х называется областью определения

Множество У называется областью значения

Если элементами х и у являются действительные числа то функция называется числовой

Три способа задания функции: графический, аналитический, табличный

Числовая последовательность и ее предел

Числовая последовательность – называется бесконечное количество чисел, следующих одно за другим и построенных по определенным законам

Бывает: возрастающей, убывающей, монотонной, ограниченной, неограниченной.

Число а называют пределом последовательности, если для положительного числа ε найдется такое натуральное число N, что при всех n>N выполнялось неравенство: ׀х_n-а׀<ε

Подпоследовательность. Теорема Больцано-Вейерштрасса

Подпоследовательность последовательности — это последовательность  , где — возрастающая последовательность элементов множества натуральных чисел. Иными словами, подпоследовательность получается из последовательности удалением конечного или счётного числа элементов.

Теорема. Из любой ограниченной последовательности можно выявить сходящуюся подпоследовательность

Доказательство. Так как последовательность ограничена, то она имеет хотя бы одну предельную точку x. В таком случае из этой последовательности можно выделить подпоследовательность, сходящуюся к точке x.

Число е. Натуральные логарифмы

Число е – математическая константа равная 2,71828182845904523536028747…, иррациональное, основание натурального логарифма, lnx

Конечный предел функции

Предел равен конкретному числу

Бесконечный предел функции

Предел равен бесконечности

Односторонние пределы

Число В называется пределом функции слева при х→а, если для любой а последовательности аргументов функции х, значение которых остаются меньше а, последовательность значений этой функции сходится к В

Число В называется пределом функции справа при х→а, если для любой а последовательности аргументов функции х, значение которых остаются меньше а, последовательность значений этой функции сходится к В