Вектор. Проекция вектора на ось
Вектор – направленный отрезок с числовым значением
Скалярные величины характеризуются своими числовыми значениями
Векторные величины характеризуются не только значением, но и направлением
Нулевой вектор, у которого начало и конец совпадают
Вектор, длина которого = 1, называется единичным ортом
Модуль вектора – расстояние между началом и концом вектора
Векторы параллельные одной прямой называется коллинеарными
Векторы, расположенные в одной плоскости или параллельны одной и той же плоскости называются компланарные
Осью называется всякая прямая с указанным направлением.
Проекцией вектора на ось можно назвать разность координат проекции начала и конца вектора на эту ось(*косинус угла)
Линейные операции над векторами
Умножение
вектора на число
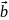=m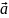
Св-ва: m(n )=(mn)
Если вектор а 0, то для любого коллинеарного вектора b существует только одно γ удовлетворяющему равенство =γ
Сложение векторов
Вектора можно сложить по правилу параллелограмма
Св-ва сложения: a+b=c+b
(a+b)+c=a+(b+c)
m(a+b)=ma+mb
Разностью двух векторов a и b называется такой вектор с, для которого c+b=a, a-b=c
Линейная зависимость и независимость системы векторов
Система векторов а1,а2,..,аn будет линейно зависимая, если можно найти такие постоянные одновременно с1,с2,…,с3 , чтобы выполнялось равенство с1а1 +с2а2+с3а3+сnаn=0. В противном случае система векторов будет линейно независимой.
Любые
два коллинеарных вектора линейно
зависимы, два неколлинеарных вектора
линейно независимы. b=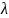
a
Теорема об единственности разложения вектора по базису. Координаты вектора. Декартова система координат.
Базис – два неколлинеарных вектора на этой плоскости
Если на плоскости е1 и е2 выбраны за базис, то любой компланарный с ними вектор а можно представить и при том единственным образом как линейную комбинацию векторов базиса а=α1е1+α2е2 .
При умножении вектора на число, его координаты умножаются на это число
При сложении двух векторов складываются их соответствующие координаты
Декартова система координат (x,y,z) в пространстве называется совокупность точки О и базиса е1,е2,е3. Прямая Ох – ось абсцисс, прямая Оу – ось ординат, Оz – ось аппликат.
Ортонормированный базис – векторы попарно ортогональны и имеют длину равную 1.
Расстояние между двумя точками
M1
(x,,y,z)
=
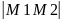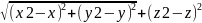
M2 (x2,y2,z2)
Деление отрезка в данном отношении
r=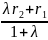
Направление вектора в пространстве
ax=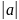
cosα
и т.д.
cos2α+cos2β+cos2γ=1
a0=
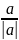=(cosα,
cosβ, cos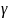
),
a0=cosαi+cosβj+cosγk
Скалярное произведение векторов и его свойства
Скалярное произведение двух векторов a и b , отличных от нуля, называется ЧИСЛО равное произведению их длин на косинус угла между ними.
ab=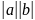
cosφ
Скалярное произведение вектора на себя называется скалярным квадратом
Св-ва: коммутативности (a,b)=(b,a)
Дистрибутивности (a+b,c)=(a,c+b,c)
Сочетательное (γ*a,b)=γ(a,b)
Скалярный квадрат всегда не отрицателен
Скалярное произведение через координаты: (a,b)=axbx+ayby+azbx