1. Виды проецирования.

Центральное (коническое) проецирование.

Центральное проецирование

Параллельное косоугольное проецирование

Параллельное прямоугольное(ортогональное) проецирование

3. Деление отрезка в заданном отношении . Теорема Фалеса о пропорциональном делении прямой.

Если одна сторона угла поделена в заданном отношении, то при парал-лельном проецировании вторая сторона угла будет поделена в том же отношении.

4.Следы прямой .

Следом прямой назы-вается точка пересечения прямой с плоскостью проекций.

Н – горизонтальный след прямой;

F – фронтальный след прямой.

5. Определение натуральной величины отрезка прямой общего положения и углов его наклона к плоскостям проекций.

• Натуральная величина отрезка равна гипоте-нузе прямоугольного треугольника, у которо-го один катет есть одна из проекций, а другой катет равен разности координат концов дру-гой проекции отрезка до оси проекций.

• Угол наклона отрезка прямой к какой-либо плоскости проекций равен углу между натуральной величиной отрезка и его проекцией на заданную плоскость проекций.

6. Взаимное расположение прямых. Конкурирующие точки скрещивающихся прямых.

7. Проецирование прямого угла без искажения.

Прямой угол проецируется без искажения на ту плоскость проекций, которой параллельна одна из его сторон. При этом другая сторона угла не перпендикулярна этой плоскости

8. Геометрическая модель плоскости. Задание плоскости на чертеже. Следы плоскости.

Плоскость задается движе-нием прямой образующей линии « n » по прямой направляющей линии « m » параллельно заданному направлению « S »

Следом плоскости называется ее пересечение с какой-либо плоскостью проекций

Р1 - горизонтальный след плоскости

Р2 - фронтальный след плоскости

Р3 - профильный след плоскости

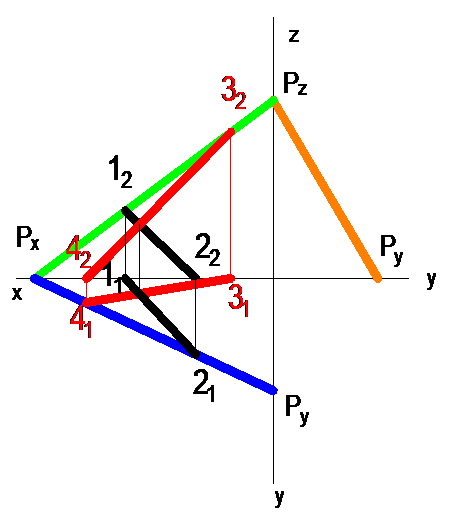
Задание плоскости на чертеже

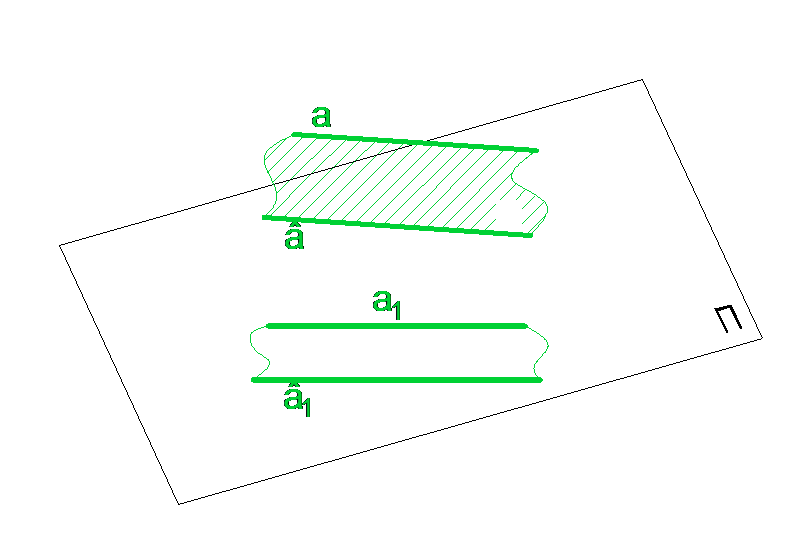
Плоскость задана двумя параллельными прямыми

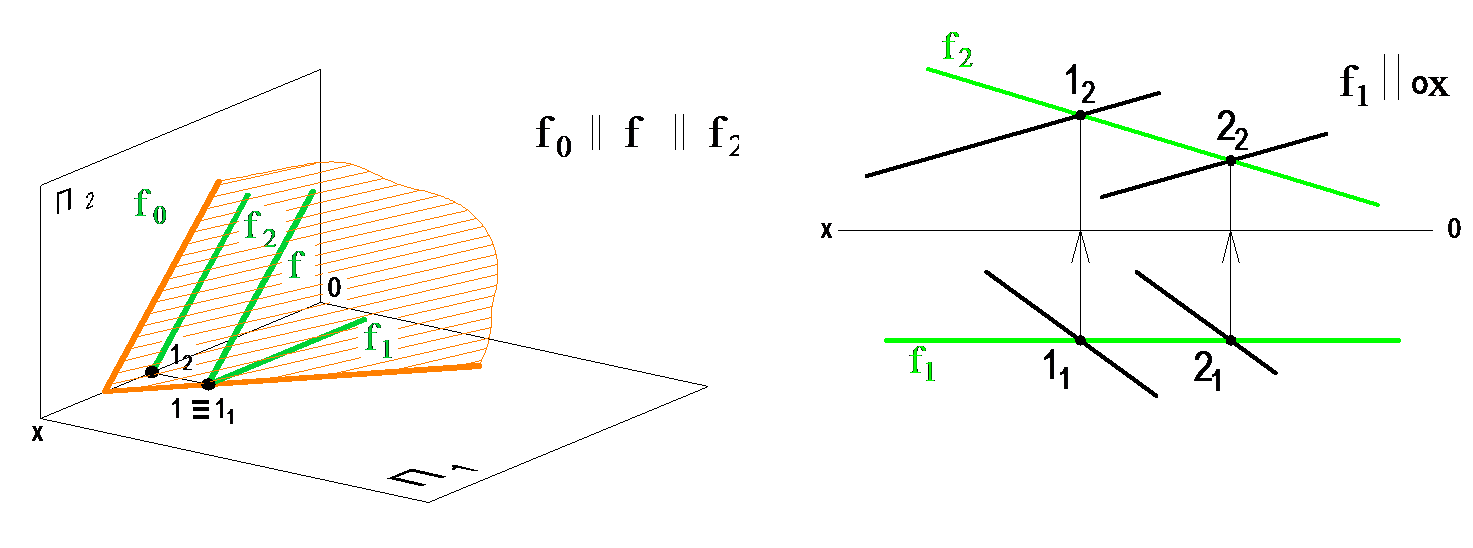
9. Главные линии плоскости: линии уровня и линии наибольшего наклона. Главные линии плоскости Горизонталь

Фронталь

Линия наибольшего уклона плоскости.Определение угла наклона плоскости общего положения к плоскостям проекций

Угол наклона плоскости общего положения к какой-либо плоскости проекций равен углу между натуральной величиной линии наибольшего уклона плоскости и ее проекцией на заданную плоскость проекций

10. Взаимное расположение плоскостей.

Плоскости параллельны между собой в том случае, если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости

Пересекающиеся плоскости

Если прямые не параллельны, то они пересекаются по прямой линии

Пересечение плоскости общего положения с горизонтально-проецирующей плоскостью

Проекция линии пересечения пло-скости общего положения с проеци-рующей плоскостью совпадает со следом проецирующей плоскости.

Пересечение плоскости общего положения с фронтально-проецирующей плоскостью

Проекция линии пересечения плоскости общего положения с проецирующей плоскостью совпадает со следом проецирующей плоскости.

Пересечение двух плоскостей

1. Рассекаем две заданные плоскости Σ и Ω вспомогатель-ной плоскостью «α».

2. Строим линии пересечения вспомогательной плоскости с заданными.

3. Находим точку пересечения полученных линий (·) I.

4. Рассекаем заданные плоскости второй вспомогательной плоскостью «β».

5. Строим линии пересечения вспомогательной плоскости с заданными.

6. Находим точку пересечения полученных линий (·) II.

7. Соединяем точки I и II, получаем линию пересечения плоскостей.

11. Взаимное расположение прямой и плоскости. Взаимно перпендикулярные прямые и плоскости.

Прямая принадлежит плоскости

Прямая принадлежит плоскости в том случае, если она проходит через две точки, принадлежащие этой плоскости.

Прямая, параллельная плоскости

Прямая параллельна плоскости в том случае, если она параллельна прямой, лежащей в этой плоскости

Пересечение прямой с плоскостью

Если прямая не лежит в плоскости и не параллельна ей, то она пересекается с плоскость.

12. Преобразование проекций. Способы: вращения (вокруг проецирующих осей и линий уровня), плоскопараллельного перемещения, замены плоскостей проекций).

Замена плоскостей проекций.

Сущность метода замены плоскостей проекций состоит в том, что предмет остается неподвижен, а плоскости проекций принимают положение, удобное для решения задачи.

Вращение вокруг проецирующих осей

Сущность метода вращения вокруг проецирующих осей состоит в том, что все точки фигуры движутся по окружностям в плоскостях, перпенди-кулярных к оси вращения, параллельно плоскости проекций, которой перпендикулярна ось вращения.

Плоско – параллельное перемещение

Сущность метода плоско-Параллельного перемещения Состоит в том, что все точки Фигуры движутся в плоскостях, Параллельных между собой

13.Геометрические модели поверхностей. Принципы образования, определитель , каркас поверхности.

Кинематический способ образования поверхностей

При кинематическом способе образования поверхности образующая линия « n » дви-жется по направляющей линии « m » по заданному направлению « S »

Пирамидальная поверхность

Поверхность образуется движением прямолинейной образующей « а »,

закрепленной в точке « S » по ломаной направляющей « m ».

Призматическая поверхность

Призматическая поверхность образуется движением прямолинейной

образующей « n » по ломаной направляющей « m » параллельно заданному направлению « S ».

Цилиндрическая поверхность

Цилиндрическая поверхность образуется движением прямоли-нейной образующей « n » по криволинейной направляющей « m ». Линия « а » - пересечение поверхности с плоскостью проекций

Торсовая поверхность(Поверхность с ребром возврата)

Торсовой поверхностью называется линейчатая поверхность, образованная множеством положений движущейся прямой образующей « n », касательной к пространственной кривой линии « m ».

Винтовая поверхность(Прямой геликоид)

Винтовая поверхность образуется вращательно-поступательным движе-нием прямолинейной образующей « n » по двум направляющим, одна из кото-рых ось вращения « i », а другая – винтовая линия « m ».

Поверхности Каталана.Цилиндроид

Цилиндроид образуется движением прямолинейной образующей (l) по

двум криволинейным направляющим (mn) параллельно некоторой пло-

скости параллелизма Σ.

Коноид

Коноид образуется движением прямолинейной образующей (l) по двум направляющим (mn), одна из которых – прямая линия, а другая – кривая, параллельно некоторой плоскости параллелизма Σ.

Гиперболический параболоид(Косая плоскость)

Гиперболический параболоид образуется движением прямолинейной образующей (l) по двум прямолинейным направляющим (mn) парал-лельно некоторой плоскости параллелизма Σ.

Поверхность вращения

Поверхность образуется вращением криволинейной образующей

вокруг осевой линии.