Вопрос 5.
Средняя
величина.
Средняя величина представляет собой
обобщенную характеристику изучаемого
признака в исследуемой совокупности,
отражающая ее типический уровень в
расчете на единицу совокупности в
конкретных условиях места и времени.
Существуют
две разновидности средних величин:
степенные (средняя арифметическая,
средняя гармоническая, средняя
геометрическая, средняя квадратическая);
структурные (мода, медиана, квартили,
децили).
Математическая
статистика выводит различные средние
из формул степенной средней:
где

средняя величина; x
– отдельные варианты (значения
признаков); z
– показатель степени (при z
= 1 – средняя арифметическая, z
= 0 средняя геометрическая, z
= - 1 – средняя гармоническая, z
= 2 – средняя квадратическая).
средняя
арифметическая.
Она исчисляется в тех случаях, когда
объем осредняемого признака образуется
как сумма его значений у отдельных
единиц изучаемой статистической
совокупности.
В
зависимости от характера исходных
данных средняя арифметическая определяется
различными способами:
Если
данные несгруппированные, то расчет
ведется по формуле простой средней
величины
 ,
,
|
Если
значение признака встречается несколько
раз, то среднюю величину находят по
формуле для сгруппированных данных и
средняя величина будет называться
среднеарифметическая взвешенная.

|
Средняя
гармоническая. Средняя
гармоническая это величина обратная
средней арифметической. Ее используют,
когда статистическая информация не
содержит частот по отдельным вариантам
совокупности, а представлена как их
произведение (М= xf).
Средняя гармоническая будет
рассчитываться по формуле 3.5

Средняя
геометрическая.
Формулы
для расчета следующие
 – для невзвешенных
значений,
– для невзвешенных
значений,
|
(5.5)
|
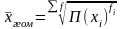 – взвешенная,
– взвешенная,
|
(5.6)
|
где
 –
варианты осредняемого признака;
–
варианты осредняемого признака;
 –
произведение вариантов; f
– частота
вариантов.
–
произведение вариантов; f
– частота
вариантов.
Средняя
квадратическая.
Формула
средней квадратической используется
для измерения степени колеблемости
индивидуальных значений признака
вокруг средней арифметической в
рядах распределения. Так, при расчете
показателей вариации среднюю
вычисляют из квадратов отклонений
индивидуальных значений признака
от средней арифметической величины.
Средняя
квадратическая величина рассчитывается
по формуле

Свойства
средней арифметической. Средняя
арифметическая обладает некоторыми
свойствами, которые позволяют
упрощать вычисления, рассмотрим
их.
Средняя
арифметическая из постоянных
чисел равна этому постоянному
числу.
Если х = а.
Тогда
 .
.
Если
веса всех вариантов пропорционально
изменить, т.е. увеличить или
уменьшить в одно и то же число раз,
то средняя арифметическая нового
ряда от этого не изменится.
Если все веса
f
уменьшить в k
раз, то
 .
.
3.
Сумма положительных и отрицательных
отклонений отдельных вариантов
от средней, умноженных на веса,
равна нулю, т.е.

Если
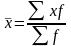 ,
то
,
то
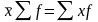 .
Отсюда
.
Отсюда
 .
.
Если
все варианты уменьшить или увеличить
на какое- либо число, то средняя
арифметическая нового ряда
уменьшится или увеличится на
столько же.
Уменьшим все
варианты x
на a,
т.е. x´
= x
– a.
Тогда

Среднюю
арифметическую первоначального
ряда можно получить, прибавляя к
уменьшенной средней ранее вычтенное
из вариантов числа a,
т.е.
 .
.
5. Если все
варианты уменьшить или увеличить
в k
раз, то средняя арифметическая
нового ряда уменьшится или увеличится
во столько же, т.е. в k
раз.
Пусть
 ,
тогда
,
тогда
 .
.
Отсюда
 ,
т.е. для получения средней
первоначального ряда среднюю
арифметическую нового ряда (с
уменьшенными вариантами) надо
увеличить в k
раз.
,
т.е. для получения средней
первоначального ряда среднюю
арифметическую нового ряда (с
уменьшенными вариантами) надо
увеличить в k
раз.
|
|
(5.4)
|
|
|
|

 средняя величина; x
– отдельные варианты (значения
признаков); z
– показатель степени (при z
= 1 – средняя арифметическая, z
= 0 средняя геометрическая, z
= - 1 – средняя гармоническая, z
= 2 – средняя квадратическая).
средняя величина; x
– отдельные варианты (значения
признаков); z
– показатель степени (при z
= 1 – средняя арифметическая, z
= 0 средняя геометрическая, z
= - 1 – средняя гармоническая, z
= 2 – средняя квадратическая).


 ,
,

 – для невзвешенных
значений,
– для невзвешенных
значений,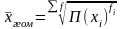 – взвешенная,
– взвешенная, –
варианты осредняемого признака;
–
варианты осредняемого признака;
 –
произведение вариантов; f
– частота
вариантов.
–
произведение вариантов; f
– частота
вариантов.
 .
. .
.
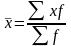 ,
то
,
то
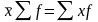 .
Отсюда
.
Отсюда
 .
.
 .
. ,
тогда
,
тогда
 .
. ,
т.е. для получения средней
первоначального ряда среднюю
арифметическую нового ряда (с
уменьшенными вариантами) надо
увеличить в k
раз.
,
т.е. для получения средней
первоначального ряда среднюю
арифметическую нового ряда (с
уменьшенными вариантами) надо
увеличить в k
раз.