14. Кинетическая энергия вращающегося тела. Закон сохранения момента импульса и его связь с изотропностью пространства.
Кинетическая энергия вращательного движения — энергия тела, связанная с его вращением.
Основные
кинематические характеристики
вращательного движения тела —
его угловая
скорость (
)
и угловое
ускорение.
Основные динамические характеристики
вращательного движения — момент
импульса относительно
оси вращения z:
и кинетическая энергия
где Iz — момент инерции тела относительно оси вращения.
Похожий пример можно найти при рассмотрении вращающейся молекулы с главными осями инерции I1, I2 и I3. Вращательная энергия такой молекулы задана выражением
где ω1, ω2, и ω3 — главные компоненты угловой скорости.
В общем случае, энергия при вращении с угловой скоростью находится по формуле:
,
где 
— тензор
инерции.
Еще одной важной векторной величиной, характеризующей механическое состояние системы, является момент импульса.
Момент
импульса частицы с импульсом 
относительно
точки О определяется как:
,
(9.1)
где 
–
радиус-вектор, характеризующий положение
частицы относительно точки О (рис. 9.1).
Определенный вектор 
перпендикулярен
векторам
, 
и
составляет с ними правую тройку. Его
величина равна
9.1рис
9.2
рис
где ℓ – длина перпендикуляра, опущенного из точки О на направление импульса, и называется плечом импульса (рис. 9.1). Продифференцируем момент импульса по времени:
.
В основе закона сохранения импульса лежит однородность пространства, т. е. одинаковость свойств пространства во всех точках (симметрия по отношению к сдвигу начала координат). Одинаковость следует понимать в том смысле, что параллельный перенос замкнутой системы из одного места пространства в другое, без изменения взаимного расположения и скоростей частиц, не изменяет механические свойства системы. · В основе закона сохранения момента импульса лежит изотропия пространства, т. е. одинаковость свойств пространства по всем направлениям (симметрия по отношению к повороту осей координат). Одинаковость следует понимать в том смысле, что поворот замкнутой системы, как целого, не отражается на её механических свойствах.
15. Образование стоячих волн. Уравнение стоячей волны и его анализ. Узлы и пучности стоячей волны
Рассматривая бегущую волну на резиновом шнуре, мы считали, что этот шнур не имеет второго конца. А что будет происходить, если второй конец шнура закрепить на жесткой стенке?
Если послать вдоль шнура единственный импульс, то он добежит до стены, отразится и побежит назад. Величина импульса вследствие затухания постепенно уменьшается
Если один конец шнура будет совершать гармонические колебания, то по шнуру побежит волна, достигнув стены будет от нее отражаться и навстречу бегущей к стене волне побежит волна отраженная. В результате на любом участке шнура встречаются две волны, бегущие в противоположные стороны. Вызванные ими колебания складываются. Частоты этих колебаний одинаковы, а амплитуды почти одинаковы, если затухание колебаний вдоль шнура невелико. Но фазы колебаний различны. Ведь волна падающая и отраженная проходят различные пути до данного участка шнура.
Кроме
того, при отражении волны от закрепленного
конца шнура происходит изменение фазы
волны, изменяется знак смещения, что
означает изменение фазы волны на 
.
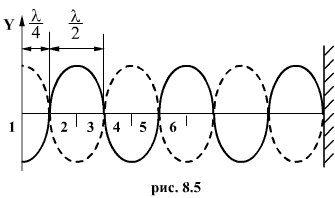
На
рисунке
пунктирамми показаны две волны бегущие
навстречу друг другу, через промежутки
времени, равные четверти периода. За
четверть периода каждая из волн
перемещается на 
.
Сплошной линией показаны результитрующие
колебания точек шнура, которые возникают
вследствие сложения колебаний.
Когда в точке шнура складываются колебания с одинаковыми фазами, то отклонение точки от положения равновесия, вызванное одной волной, прибавляется к такому же отклонению, вызванному другой волной. В результате амплитуда колебаний удваивается. Такие точки называютсяпучностями.
Если же в какой-либо точке складываются колебания с противоположными фазами, то точка эта остается в покое. Потому, что перемещения точки, вызванные падающией и отраженной волной, направлены в противоположные стороны и вычитаются друг из друга. Такие точки называютсяузлами.
Когда две одинаковые волны с равными амплитудами и периодами распространяются навстречу друг другу, то при их наложении возникают стоячие волны. Стоячие волны могут быть получены при отражении от препятствий. Допустим, излучатель посылает волну к препятствию (падающая волна). Отраженная от него волна наложится на падающую волну. Уравнение стоячей волны можно получить сложением уравнения падающей волны
и
уравнения
отраженной волны
Отраженная
волна движется в направлении,
противоположном падающей волне, поэтому
расстояние х берем со знаком минус.
Смещение точки, которая участвует
одновременно в двух колебаниях, равно
алгебраической сумме 
.
После несложных преобразований,
получаем
Это
уравнение стоячей волны определяет
смещение любой точки волны
Вывод уравнения стоячей волны.
Рассмотрим две волны с одинаковыми амплитудами и частотами, которые распространяются навстречу друг другу:
Уравнение первой волны
(40)
(41)
При наложении двух волн друг на друга:
(42)
(43)
(44)
-уравнение стоячей волны
-амплитуда стоячей волны
Координаты узлов и пучностей.
Пучности –
точки, в которых амплитуда стоячей
волны максимальна 
:
-Координаты
пучности
Узлы
стоячей волны –
точки, в которых амплитуда стоячей
волны равна нулю 
:
-координаты
узлов
Величина
не зависит от времени и определяет
амплитуду любой точки с координатой
х. Каждая точка совершает гармоническое
колебание с периодом Т. Амплитуда
Аст для каждой точки вполне определена.
Но при переходе от одной точки волны к
другой она изменяется в зависимости
от расстояния х. Если придавать х
значения, равные 
и
т.д., то при подстановке в уравнение
(8.16) получим 
.
Следовательно, указанные точки волны
остаются в покое, т.к. амплитуды их
колебаний равны нулю. Эти точки называются
узлами стоячей волны. Точки, в которых
колебания происходят с максимальной
амплитудой, называются пучностями.
Расстояние между соседними узлами (или
пучностями) называются длиной стоячей
волны и равно
где λ - длина бегущей волны