30. Средняя кинетическая энергия молекул. Молекулярно-кинетическое толкование абсолютной температуры.

Сравнивая уравнение состояния идеального газа и основное уравнение кинетической теории газов, записанные для одного моля (для этого число молекул N возьмём равным числу Авогадро N_А), найдём среднюю кинетическую энергию одной молекулы:

 и  .

Откуда

.           (31)

Средняя кинетическая энергия поступательного движения молекулы не зависит от её природы и пропорциональна абсолютной температуре газа T. Отсюда следует, что абсолютная температура является мерой средней кинетической энергии молекул.

 Молекулярно-кинетическое толкование абсолютной температуры. С точки зрения молекулярно-кинетической теории абсолютная температура есть величина, пропорциональная средней энергии поступательного движения молекулы. < _пост>=3/2kT.

31. Термодинамическая система. Термодинамические параметры. Равновесные состояния и процессы, их изображения на термодинамических диаграммах. Внутренняя энергия системы - функция состояния. Теплообмен и работа - способы передачи энергии.

Термодинамическая система — это некая физическая система, состоящая из большого количества частиц, способная обмениваться с окружающей средой энергией и веществом. Также обычно полагается, что такая система подчиняется статистическим закономерностям. Для термодинамических систем справедливы законы термодинамики.

Термодинамическая система — совокупность макроскопических тел, которые могут взаимодействовать между собой и с др. телами (внешней средой) — обмениваться с ними энергией и веществом; состоит из столь большого числа структурных частиц (атомов, молекул), что её состояние можно характеризовать макроскопическими параметрами: плотностью, давлением, концентрацией веществ, образующих термодинамическую систему, и т.д.

Параметры состояния, термодинамические параметры — физические величины, характеризующие состояние термодинамической системы: температура, давление, удельный объём, намагниченность,электрическая поляризация и др. Различают экстенсивные параметры состояния, пропорциональныемассе системы:

1.объём,

2.внутренняя энергия,

3.энтропия,

4.энтальпия,

5.энергия Гиббса,

6.энергия Гельмгольца (свободная энергия),

и интенсивные параметры состояния, не зависящие от массы системы:

7.давление,

8.температура,

9.концентрация,

10.магнитная индукция и др.

Не все параметры состояния независимы, так что равновесное состояние системы можно однозначно определить, установив значения ограниченного числа параметров состояния.

диагра́мма состоя́ния

(фазовая диаграмма), графическое изображение соотношения между параметрами состояния термодинамически равновесной системы (температурой, давлением, составом и др.). Диаграмма состояния позволяет определить, сколько фаз и какие конкретно фазы образуют систему при данных температуре, давлении, составе и других параметрах состояния. Диаграммы состояния используют на практике в материаловедении, физико-химическом анализе и т. д.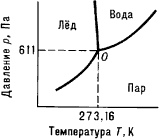 

Равнове́сный тепловой процесс — тепловой процесс, в котором система проходит непрерывный ряд бесконечно близких равновесных термодинамических состояний.

Равновесный тепловой процесс называется обратимым, если его можно провести обратно и в телах, окружающих систему, не останется никаких изменений.

Реальные процессы изменения состояния системы всегда происходят с конечной скоростью, поэтому не могут быть равновесными. Реальный процесс изменения состояния системы будет тем ближе к равновесному, чем медленнее он совершается, поэтому равновесные процессы называют квазистатическими.

Термодинамическое равновесие — предельное состояние, к которому стремится термодинамическаясистема, изолированная от внешних воздействий, то есть в каждой точке системы устанавливается термическое, механическое и химическое равновесие (происходит выравнивание температуры и давления, и все возможные химические реакции достигают состояния, когда в каждом элементарном химическом процессе скорость прямой реакци равна скорости обратной).

Вну́тренняя эне́ргия тела (обозначается как E или U) — это сумма энергий молекулярных взаимодействий и тепловых движений молекулы. Внутренняя энергия является однозначной функцией состояния системы. Это означает, что всякий раз, когда система оказывается в данном состоянии, её внутренняя энергия принимает присущее этому состоянию значение, независимо от предыстории системы. Следовательно, изменение внутренней энергии при переходе из одного состояния в другое будет всегда равно разности между ее значениями в конечном и начальном состояниях, независимо от пути, по которому совершался переход.

Внутреннюю энергию тела нельзя измерить напрямую. Можно определить только изменение внутренней энергии:

Где. 1.  — подведённое к телу количество теплоты, измеренное в джоулях.2. ^[1] — работа, совершаемая телом против внешних сил, измеренная в джоулях

Эта формула является математическим выражением первого начала термодинамики

Для квазистатических процессов выполняется следующее соотношение:

где1.  — температура, измеренная в кельвинах2  — энтропия, измеренная в джоулях/кельвин3.  — давление, измеренное в паскалях4.  — химический потенциал5.  — количество частиц в системе

Внутренняя энергия термодинамическая функция состояния системы, ее энергия, определяемая внутренним состоянием. Внутренняя энергия складывается в основном из кинетической энергии движения частиц (атомов, молекул, ионов, электронов) и энергии взаимодействия между ними (внутри- и межмолекулярной). На внутреннюю энергию влияет изменение внутреннего состояния системы под действием внешнего поля; во внутреннюю энергиювходит, в частности, энергия, связанная с поляризацией диэлектрика во внешнем электрическом поле и намагничиванием парамагнетика во внешнем магнитном поле. Кинетическая энергия системы как целого и потенциальная энергия, обусловленная пространственным расположением системы, во внутреннюю энергию не включаются. В термодинамике определяется лишь изменение внутренней энергии в различных процессах. Поэтому внутреннюю энергию задают с точностью до некоторого постоянного слагаемого, зависящего от энергии, принятой за нуль отсчета.

Внутренняя энергия U как функция состояния вводится первым началом термодинамики, согласно которому разность между теплотой Q, переданной системе, и работой W, совершаемой системой, зависит только от начального и конечного состояний системы и не зависит от пути перехода, т.е. представляет изменение фуникции состояния ΔU

Внутренняя энергия есть сумма всех видов энергии движения и взаимодействия частиц, составляющих рассматриваемое тело, вычисленная в системе координат, в которой центр масс тела неподвижен. Поэтому внутренняя энергия не содержит кинетическую энергию движения тела как целого и ее потенциальную энергию во внешнем поле сил. Таким образом, внутренняя энергия складывается из кинетической энергии движения молекул, составляющих тело, кинетической энергии атомов внутри молекул, потенциальной энергии взаимодействия между молекулами, потенциальной энергии взаимодействия между атомами в молекуле, а также внутриатомной и внутриядерной энергии. (Последние две части внутренней энергии в курсах молекулярной физики не рассматриваются.)

Термодинамика не исследует внутреннее движение частиц и силы взаимодействия между ними, поэтому в рамках этой науки невозможно получить математическое выражение для вычисления внутренней энергии термодинамической системы. Это выражение находят из специальных опытов или из статистической теории.

Наиболее просто получить выражение для вычисления внутренней энергии идеального газа. Так как молекулы идеального газа не взаимодействуют между собой, то его внутренняя энергия U равна

(4.2.1)

где N – число молекул в газе, а средняя энергия  , приходящаяся на одну молекулу, согласно теореме распределения, равна

(4.2.2)

где i – число степеней свободы молекулы. Подставляя последнее выражение в (4.2.1), получим

(4.2.3)

Умножив и разделив правую часть формулы (4.2.3) на число Авогадро   , получим

(4.2.4)

Учитывая, что   , соотношение (4.2.4) можно представить в виде:

(4.2.5)

Как видно из формулы (4.2.4), внутренняя энергия идеального газа,зависит от его температуры T, количества молей   и от сложности строения молекулы, характеризуемой ее числом степеней свободы i.

Внутренняя энергия должна являться функцией равновесного состояния системы, т. е. функция U должна однозначно определяться термодинамическими параметрами, характеризующими это состояние. Если бы это было не так, и в некотором состоянии система частиц могла обладать разными значениями внутренней энергии, т. е. последняя не была бы однозначной функцией состояния, то разность этих значений внутренней энергии можно было бы превратить в работу, не изменяя состояния тела, что противоречит закону сохранения энергии.