18. Сложение одинаково направленных гармонических колебаний равных частот. Уравнение, амплитуда и фаза результирующего колебания.

Используя метод вращающегося вектора амплитуды сложим гармонические колебания одного направления и одинаковой частоты:

Построим векторные диаграммы этих колебаний (рис.1). Так как векторы А1 и А2 вращаются с одинаковой угловой скоростью ω0, то разность фаз (φ1 - φ2) между ними остается постоянной.

Уравнение результирующего колебания имеет вид:

 

Амплитуда А результирующего колебания при этом равна:

 

Амплитуда А результирующего колебания зависит от разности фаз (φ1 - φ2) складываемых колебаний (рис.2):

     1.  если (φ1 - φ2) = ± 2mπ  (m = 0, 1, 2, 3, ...), то амплитуда результирующего колебания равна сумме амплитуд складываемых колебаний:

     2.  если (φ1 - φ2) = ± (2m+1)π  (m = 0, 1, 2, 3, ...), то амплитуда результирующего колебания равна разности амплитуд складываемых колебаний:

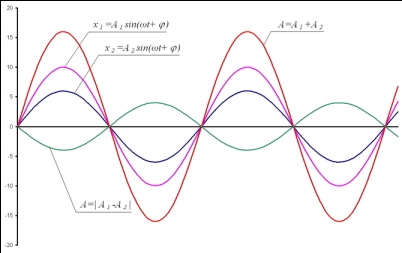
рис.2

 

Начальная фаза результирующего колебания находится по формуле:

19. Сложение одинаково направленных гармонических колебаний различных частот. Биения.

Гармонические колебания, частоты которых различны ( ), некогерентны, так как разность их фаз, равная  , непрерывно изменяется с течением времени. При наложении таких колебаний получаются негармонические результирующие колебания.  Векторы амплитуд A1 и A2 складываемых колебаний (рис. 9.1) вращаются с разными угловыми скоростями, так что построенный на них параллелограмм непрерывно деформируется, а его диагональ – вектор A результирующих колебаний – изменяется по длине и вращается с переменной угловой скоростью.

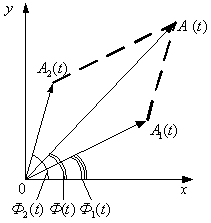
Рис. 9.1. Сложение двух одинаково направленных гармонических колебаний Результирующим колебаниям:   соответствует вектор, проекция которого на вертикальную ось   равна:

   (9.1) По теореме косинусов

    а                                      (9.2)

     

 Бие́ния — явление, возникающее при наложении двух гармонических колебаний, близких по частоте, выражающееся в периодическом уменьшении и увеличении амплитуды суммарного сигнала. Биения модулируются по амплитуде. Распространение такого вида колебаний менее эффективно. Частота изменения амплитуды суммарного сигнала равна разности частот двух исходных сигналов.

20. Энергия волны.

Найдем изменение энергии малого объема dV упругой среды, связанное с распространением в среде плоской волны, которая задана уравнением

(8.9

Ввиду малости объема dV можно считать, что все находящиеся в нем частицы среда колеблются в одной фазе, так что их скорости одинаковы и равны

Поэтому кинетическая энергия объема среды dV, связанная с колебательным движением, равна

где ρ - плотность среды. Из (8.9) следует Поэтому

8.10

Подсчитывая работу деформации объема dV среды при волновом движении (деформация сдвига в случае поперечной волны и деформации объемного сжатия в случае продольной волны), можно показать, что потенциальная энергия dWп объема dV среды равна его кинетической энергии. Полная механическая энергия dW колебательного движения элементарного объема dV упругой среды равна сумме его кинетической и потенциальной энергии

8.11

Энергия волны

        При распространении волны в пространстве от какого-либо источника происходит и распространение энергии; частицы среды, вовлекаемые в колебательное движение, получают энергию от волны. Проследим, как энергия от источника распространяется в пространстве.

        Предположим, что наш источник - плоская металлическая мембрана, колеблющаяся с определённой частотой. Колебаться мембрану заставляет вынуждающая сила, в данном случае - переменное (синусоидальное) магнитное поле. Мембрана, в свою очередь, заставляет колебаться частицы воздуха, и в пространстве за мембраной распространяется плоская продольная упругая волна.

        Энергия мембраны есть энергия её движения, то есть чисто кинетическая энергия. (Мы полагаем мембрану безинерционной и неупругой, её колебания в точности соответствуют колебаниям магнитного поля.) Среду, в которой распространяется волна (воздух) будем считать идеальной, не поглощающей волну (реально это справедливо для небольших участков пространства, в пределах которых диссипацией энергии можно пренебречь).

        Поскольку мембрана колеблется по синусоидальному закону, её энергия (кинетическая) также будет периодически меняться со временем, но с удвоенной частотой (энергия пропорциональна квадрату скорости и не зависит от её знака). Следовательно, энергия источника будет поступать в среду циклически, с частотой, в два раза большей частоты колебаний источника.

        Какие формы принимает энергия в среде за мембраной? Во-первых, это кинетическая энергия частиц воздуха, пришедших в движение; во-вторых, поскольку среда упругая, это потенциальная энергия деформации воздуха. Причём и кинетическая, и потенциальная энергия в любой точке пространства изменяются абсолютно синхронно во времени: когда кинетическая энергия достигает максимума, то и потенциальная энергия максимальна, и наоборот. В самом деле, проследим за слоем воздуха непосредственно за мембраной: когда скорость мембраны максимальна, максимальна и скорость частиц воздуха, но при этом мы имеем и максимальное сжатие воздуха за мембраной. Когда скорость мембраны равна нулю (два раза за период), энергия мембраны равна нулю, в волну в эти моменты энергия не поступает.

        Пусть v* - скорость частиц среды в какой-то момент времени в какой-то точке пространства (или, точнее, в физически малом объёме dV). Объёмная плотность кинетической энергии Wk запишется (r - плотность среды):

Объёмная плотность потенциальной энергии упруго деформируемой среды равна:

 - фазовая скорость волны,  - относительная деформация среды.

Учитывая, что:

               

имеем:

        Причём в каждой точке пространства объёмные плотности кинетической и потенциальной энергий равны. Этот вывод справедлив для любых волн в упругих средах: полная механическая энергия волны в каждой точке есть сумма двух равных слагаемых, потенциальной и кинетической энергий.

        Из вышеприведённой формулы следует, что среднее за период значение объёмной плотности энергии равно: