- •Поверхностная энергия раздела фаз
- •Метод Вильгельми
- •Метод лежачей капли
- •Метод определения по форме висячей капли.
- •Метод вращающейся капли
- •Метод Дю Нуи (метод отрыва кольца).
- •Сталагмометрический, или метод счета капель.
- •Метод максимального давления пузырька (метод Ребиндера).
- •Метод осциллирующей струи
- •Метод стоячих волн
- •Метод бегущих волн
- •Нормируемые показатели пав
- •3) Гидрофильно-липофильный баланс (глб).
- •4) Точка Крафта
- •Факторы адгезионного взаимодействия
- •Молекулярная (адсорбционная) адгезия.
- •Химическая адгезия.
- •Методы определения адгезионной прочности
- •Придание поверхности определенного рельефа,
- •Химическое модифицирование поверхности с формированием активных групп,
- •Создание прочной оксидной пленки на поверхности.
- •2 Абсолютная адсорбция.
- •3 Удельная адсорбция.
- •Уравнение монослойной адсорбции Ленгмюра:
- •Уравнение Никольского.
- •Уравнение изотермы адсорбции теории бэт
- •Уравнение в Ленгмюра вида:
- •Переход электрона с катиона более низкой валентности на катион более высокой валентности
- •Электронные переходы, вызванные дефектами кристаллической структуры
- •Электронные переходы, обуславливающие цвет органических соединений.
- •1 Электрическая проводимость
Уравнение Никольского.
При ионообменной адсорбции происходит стехиометрический обратимый обмен ионов между объемом раствора электролитов и адсорбентом.
Процессы ионного обмена на твердой поверхности характеризуются уравнением Б.П.Никольского:
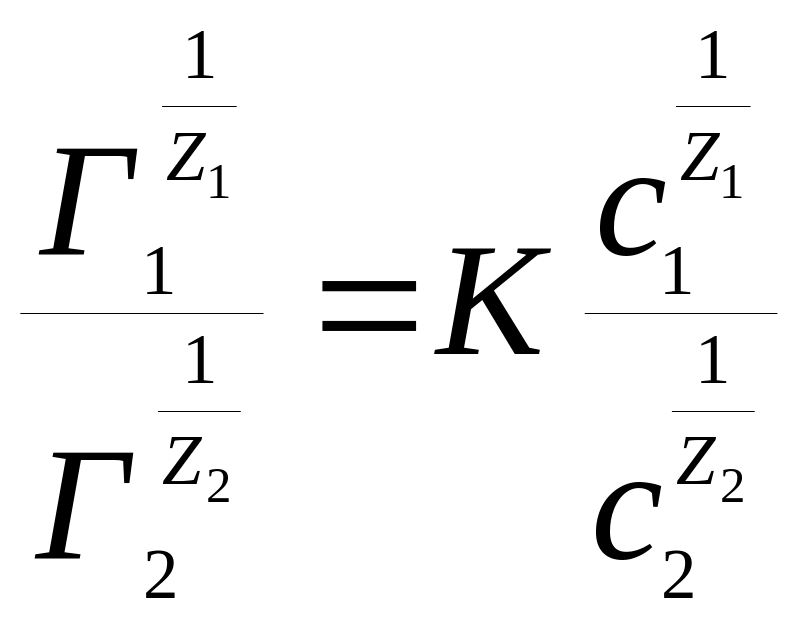
где
![]() и
и
![]() - количество ионов, поглощенных
поверхностью сорбента (кмоль/кг),
- количество ионов, поглощенных
поверхностью сорбента (кмоль/кг),
![]() и
и
![]() - равновесные концентрации ионов в
растворе (кмоль/
- равновесные концентрации ионов в
растворе (кмоль/![]() ),
),
К – константа обмена, зависящая от способности ионов к адсорбции на данном сорбенте.
Графически уравнение Б.П.Никольского изображается прямой, тангенс угла наклона которой и представляют величину константы К.
Уравнение изотермы адсорбции теории бэт
При адсорбции газов и паров на поверхности многих адсорбентов образуется полимолекулярный адсорбционный слой. В этих случаях теория Ленгмюра неприменима и для различного рода расчетов пользуются теорией БЭТ.
Теория БЭТ устанавливает следующую зависимость между Г и p :
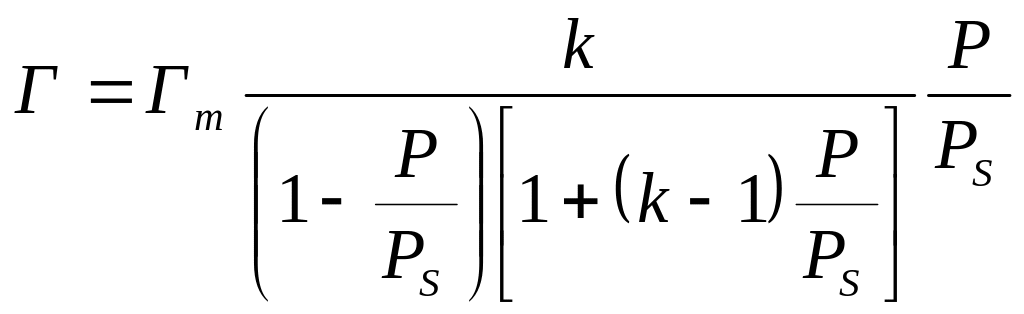
Гm-адсорбционная емкость насыщенного монослоя, определяющаяся размером “посадочной” площадки молекулы газа, т.е. площадью, которую она занимает в насыщенном монослое;
k-константа, зависящая от энергии взаимодействия молекул в адсорбционном слое;
PS-давление насыщенного пара.
Уравнение в Ленгмюра вида:
![]()
Va – адсорбционный объем,
V – равновесный объем адсорбата.
k-константа, пропорциональная энергии взаимодействия молекул газа с адсорбентом.
р – давление (равновесное)
можно привести к виду:
![]()
![]()
В таком виде уравнение БЭТ является уравнением прямой линии, если функцией считать величину, стоящую слева, а аргументом —P/PS.
Теория БЭТ используется для расчета удельной поверхности адсорбентов (поверхности единицы массы адсорбента) по экспериментально полученной изотерме адсорбции.
Для определения удельной поверхности адсорбента S строят график зависимости P/PS/(1- P/PS)Г от P/PS.
По угловому коэффициенту прямой, равному, (k-1)/kГm, и, величине отрезка, отсекаемого на оси ординат при P/PS =0 и равного 1/Гmk, рассчитывают Гm.
Удельная поверхность вычисляется по формуле:
![]()
S0-площадь, занимаемая одной молекулой газа в адсорбционном слое;
Na-постоянная Авогадро.
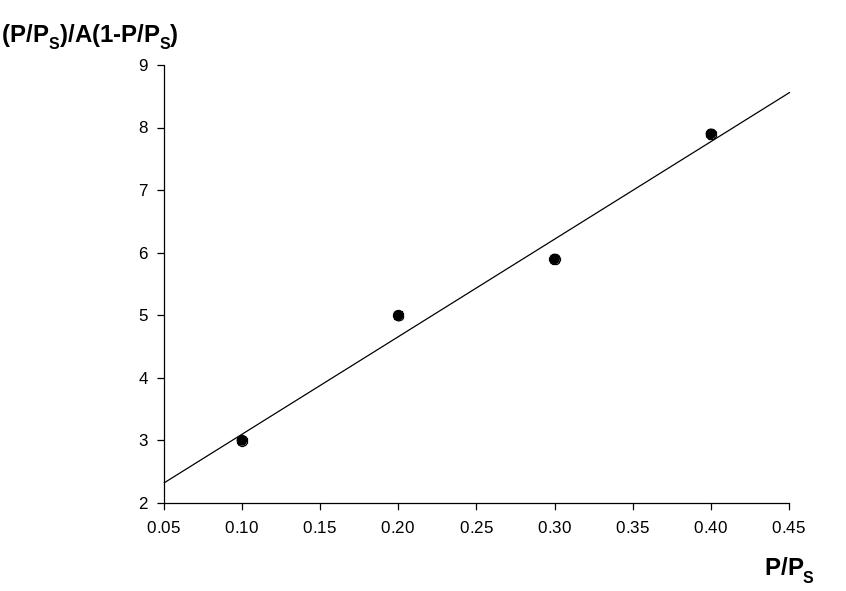
Изотерма адсорбции в координатах линейной формы уравнения БЭТ.
Для адсорбции из растворов линейная форма уравнения БЭТ выглядит таким образом:
![]()
Сs-концентрация насыщенного раствора.
Изотерму адсорбции строят так же, как и в первом случае, в координатах соответствующих этому уравнению. Аналогично вычисляется удельная поверхность:
![]()
Адсорбционное взаимодействие в адгезированных слоях
Обязательная стадия – смачивание.
Адсорбция происходит по разному в зависимости от концентрации полимера или мономера в растворе
Адсорбция из разбавленных растворов
Используется очень редко.
Разбавленными считается раствор, для которого выполняется уравнение Хаггинса:
;
ηпр = ηуд/С
Основной характеристикой адсорбции полимеров из раствора является отношение числа связанных звеньев к сумме связанных и свободных:
![]() ;
;
Величина адсорбции вычисляется формально как отношение:
![]()
![]() ;
;
![]()
![]() ;
;
Для того, чтобы найти удельную адсорбцию используют уравнение:
![]()
![]() ;
;
![]()
![]() ;
;
Это избыточная (гиббсовская) адсорбция и справедлива только для сильно разбавленных растворов.
Истинную адсорбцию можно измерить только с использованием меченых атомов при адсорбции из растворов эллипсометрически или с использованием весов Мак-Бена при адсорбции из газовой фазы, методом рассаеивания рентгеновсого излучения и др. методами (НВПО – нарушенное полное внутреннее отражение, МНВПО – многократное нарушенное полное внутреннее отражение).
Адсорбция из полуразбавленных, концентрированных растворов и расплавов
Вязкость дисперсий зависит как от вязкости жидкости, так и от количества и свойств твердой фазы, наполняющей систему. Эти величины связаны уравнением Эйнштейна:
ηc = ηж (1+2,5φ),
где ηc - вязкость суспензии;
ηж - вязкость жидкости;
φ - объемное содержание твердой фазы
Это уравнение выполняется когда:
1) частицы твердой фазы имеют сферическую форму,
2) суспензии разбавленные,
3) в системах нет взаимодействия между фазами.
В полуразбавленном растворе в равновесии находятся мицеллы и свободные молекулы.
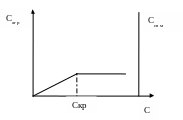
Если молекула дифильна, то Скр=ККМ, если недифильна, то это критическая концентрации агрегации.
Наступление адсорбционного равновесия определяется двумя факторами:
энергией адсорбции, т.е. прочностью адсорбционных связей;
скоростью адсорбции, которая определяется диффузией молекул или агрегатов.
Подвижность больше у отдельных молекул. Высокомолекулярные фракции (труднорастворимые) будут адсорбироваться сильнее, чем низкомолекулярные, но последние в свою очередь обладают большей подвижностью.
Оптические свойства наполненных полимерных систем
Отражение света
Внешний вид поверхности напрямую зависит от характера взаимодействия света с веществом. При падении света на поверхность происходит его отражение, поглощение и рассеяние. Это приводит к определенным цветовым ощущениям.
Отраженный
свет может быть направлен в какую-то
одну сторону или рассеян в определенном
телесном угле (![]() ).
).
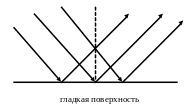
Если падающий свет отражается в одну сторону и при этом угол отражения равен углу падения, то такое отражение называется зеркальным.
![]() ;
;
где
![]() - угол падения и отражения света
соответственно (измеряются от нормали).
- угол падения и отражения света
соответственно (измеряются от нормали).
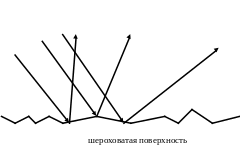
Если свет рассеивается неровностями поверхности или микронеоднородностями в ее верхнем слое, то отражение называется диффузным.
Ниже приведены схемы зеркального, диффузного отражения (рисунок ).
|
|
||
Рисунок 1 - Диффузное отражение |
|||
|
|
|
|
Рисунок - Зеркальное отражение |
|
||
В большинстве случаев имеет место смешанное отражение (рисунок 3).

Рисунок 3 – Отражение света поверхностью пигментированного материала
Таким образом, направление отраженного света играет большую роль в восприятии внешнего вида покрытия. Если имеет место высокое зеркальное отражение, то, поверхность, воспринимается блестящей, и, наоборот, если луч света отражается во всех направлениях, поверхность пигментированного лакокрасочного материала воспринимается матовой [3-7].
В соответствии с ГОСТ Р 52489 – 2005 (Материалы лакокрасочные. Колориметрия Часть 1) спектральный коэффициент отражения - отношение отраженного светового потока в полусферу к падающему потоку излучения [8].
В общем случае
коэффициент отражения
![]() складывается из коэффициентов зеркального
отражения
складывается из коэффициентов зеркального
отражения
![]() и коэффициентов диффузного отражения
и коэффициентов диффузного отражения
![]() [5]:
[5]:
![]() ;
;
В соответствии с ГОСТ 26148-84 (Фотометрия. Термины и определения) коэффициент зеркального отражения - величина, определяемая отношением зеркально отраженного потока излучения к падающему потоку излучения.
Коэффициент определяет блеск и глянец материала и зависит в первую очередь от качества его поверхности (рельефа поверхности). Изменить рельеф поверхности покрытия можно варьированием степени наполнения лакокрасочного материала, при этом в области близкой к критическому объемному содержанию (КОСП) наблюдается резкое изменение оптических свойств. Это обусловлено изменением формы полосы поглощения света из-за возможного отражения различной кратности и промежуточного проникновения света в вещество [3,4,7-11].
Коэффициент диффузного отражения - величина, определяемая отношением диффузно отраженного потока излучения к падающему потоку излучения, определяет собственно цвет покрытия и зависит от оптических свойств пигментированного материала, т.е. от коэффициентов поглощения и рассеяния света [9].
Спектральная зависимость коэффициентов диффузного отражения от длины волны («спектр отражения», «кривая отражения») является однозначной объективной характеристикой цвета пигментированных покрытий. На рисунке 4 приведены спектральные коэффициенты отражения пигментированных материалов белого, черного, синего, зеленого и красного цвета. Цвет идеального черного совпадает с осью абсцисс, цвет идеального белого образца параллелен оси абсцисс и коэффициент отражения в этом случае равен 1,0 [3,5].
1
ρ
4
5
2
3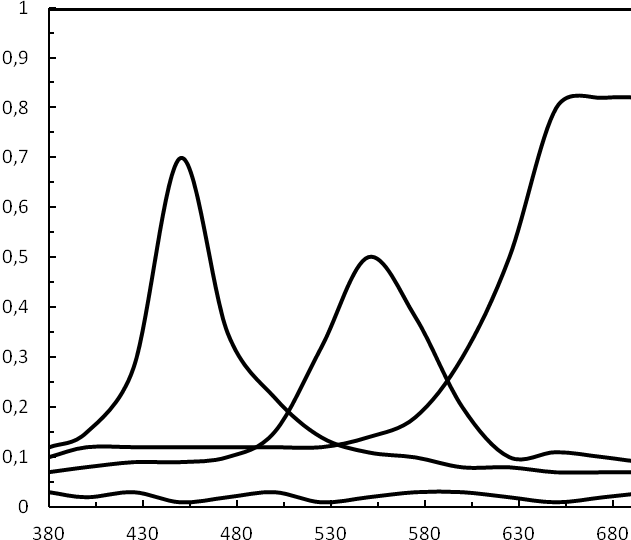
![]() ,
нм
,
нм
1 - идеальный белый (MgO), 2- черный, 3-синий, , 4- зеленый, 5 – красный
Рисунок –Спектры отражений некоторых реальных покрытий.
Рассеяние и поглощение света
Рассеяние света - это процесс преобразования света, сопровождающийся изменением направления распространения света. Направление рассеяния зависит от коэффициента преломления. Рассеяние за счет преломления увеличивается до критической точки, при которой длина волны падающего света соизмерима с размером частиц [3,4].
Рассеяние излучения внутри пигментированного лакокрасочного материала распространяется в различных направлениях, поскольку частицы пигмента имеют чаще неправильную форму и углы отражения и преломления могут принимать любые значения. Кроме рассеяния в частицах пигмента и в пленкообразователе может происходить поглощение излучения. Поглощение света – явление уменьшения энергии электромагнитного излучения в ультрафиолетовой, видимой и инфракрасной областях спектра при его распространении в веществе вследствие преобразования его энергии в другие виды энергии, а также рассеяния не в направлении потока [2,3,12].
Поглощение света подчиняется закону Бугера – Ламберта -Бера:
![]() ;
;
где I, I0 – интенсивность монохроматического света на входе и выходе слоя поглощающего вещества толщиной х,
к – коэффициент поглощения.
Отсюда следует:
![]() ;
;
Логарифм отношения интенсивности падающего света к интенсивности прошедшего света называется оптической плотностью системы [13]:
![]()
Если пигмент состоит из крупных частиц, значительно превышающих по размерам длины волн видимого света, рассеяние сводится к многократному зеркальному отражению светового потока поверхностями частиц. Свет, падающий по нормали (вертикально) к поверхности или к любой границе раздела двух сред с различными показателями преломления, согласно закону Френеля частично будет отражаться в обратном направлении.
При нормальном падении монохроматического света из среды с коэффициентом преломления n1 в среду с коэффициентом преломления n2 коэффициент отражения определяется уравнением Френеля:
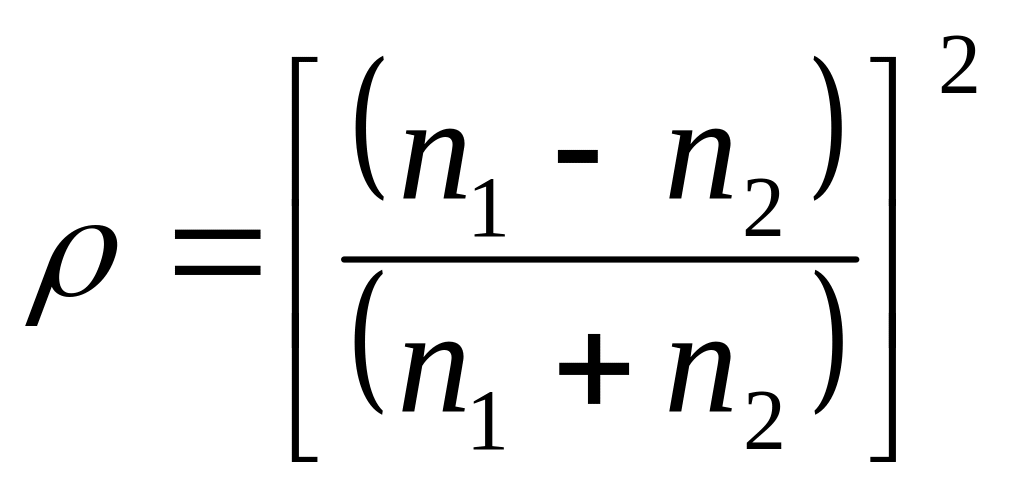
Формула Френеля справедлива в том случае, когда граница раздела двух сред гладкая, среды изотропны, угол отражения равен углу падения, а угол преломления определяется законом Снеллиуса: когда луч проходит сквозь среду с показателем преломления n1 и входит в среду с показателем преломления n2, то он отклоняется под углом в соответствии с уравнением [4]:
![]()
где iп. – угол падения,
iотр. – угол преломления.
В случае неровной поверхности, особенно когда характерные размеры неровностей одного порядка с длиной волны, большое значение имеет диффузное рассеяние света на поверхности. Таким образом, если частицы пигмента соизмеримы с длиной волны, рассеяние света не подчиняется закону Френеля.
При прохождении света через однородную среду все частицы подвергаются поляризации, зависящей от частоты электромагнитных колебаний. В результате поляризации образуются диполи с переменным электрическим моментом, которые тоже излучают свет, т.е. сами являются источниками электромагнитных колебаний. Согласно принципу Гюгейнса, свет, излучаемый диполями, распространяется в том же направлении, что и падающий поток, с интенсивностью падающего потока. Если в системе присутствуют частицы с большей или меньшей поляризуемостью, чем среда, а показатель преломления этих частиц отличается от показателя преломления среды, то диполи, получающиеся в результате поляризации, имеют другие значения дипольных моментов. Излучение этих диполей не равно излучению среды. Такое некомпенсированное излучение представляет собой рассеянный свет, интенсивность которого для сферических непоглощающих частиц определяется уравнением Рэлея :

где Is-интенсивность рассеянного света;
I0- интенсивность падающего света;
- частичная концентрация;
d- диаметр частиц;
n1 и n0 – показатель преломления частицы и среды соответственно;
- длина волны падающего света.
Согласно этому закону интенсивность рассеянного средой света обратно пропорциональна 4-й степени длины волны возбуждающего света. Именно поэтому голубые и синие лучи, имеющие меньшую длину волны по сравнению с желтыми и красными лучами рассеиваются сильнее, обуславливая тем самым голубой цвет неба [12-16].
Уравнение Рэлея справедливо только для сферических непоглощающих свет частиц (белых золей), при таких концентрациях, когда частицы не контактируют между собой.
Теория Релея успешно используется для определения среднего размера частиц водных дисперсий полимеров, используемых в лакокрасочной промышленности.
Более совершенный закон рассеяния света поглощающими свет частицами основан на теории Ми с поправками Ганса.
По теории Ми интенсивность рассеянного света для данной длины волны и данного размера частиц определяется не только соотношением показателей преломления частицы и среды, но и коэффициентом поглощения.
Согласно теории Рэлея и теории Ми, рассеяние света возрастает с ростом показателя преломления частиц дисперсной фазы. Однако, в теории Ми рассматривается рассеяние изолированными частицами и не учитывается многократное рассеяние и эффект интерференции света при большом объемном содержании пигмента, когда размеры частиц, расстояние между ними и длина волны падающего светового потока имеют один порядок.
Для частиц неправильной формы и систем с высокой концентрацией теория Ми уточнена Гансом.
Уравнение для расчета интенсивности рассеянного света Is по теории Ми имеет следующий вид [2]:
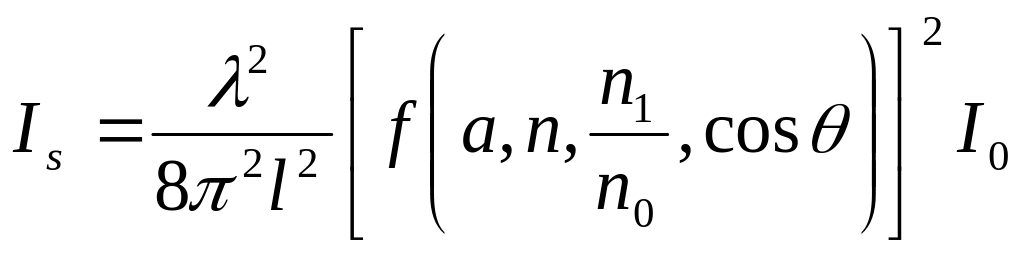
где λ длина волны;
l – расстояние от частицы до точки измерения интенсивности;
![]() ;
;
где
![]() - комплексный показатель преломления
-
- комплексный показатель преломления
-
![]() ;
;
![]() - действительная
часть, определяющая поляризацию света
(преломление света ввиду различия в
скоростях света в среде и частицах);
- действительная
часть, определяющая поляризацию света
(преломление света ввиду различия в
скоростях света в среде и частицах);
![]() - мнимая часть,
характеризующая диссипацию энергии
(рассеивание энергии в виде тепла) т.е.
поглощение света;
- мнимая часть,
характеризующая диссипацию энергии
(рассеивание энергии в виде тепла) т.е.
поглощение света;
n1, nо – комплексные показатели преломления дисперсной фазы и среды соответственно
![]() -
угол между направлениями рассеянного
и падающего света.
-
угол между направлениями рассеянного
и падающего света.
Типичная зависимость показателя преломления от длины волны для сред с областью поглощения представлена на рисунке 5.
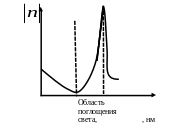
Рисунок 5 – Зависимость показателя преломления от длины волны
Модуль
![]() ;
;
имеет значения от 1 до 3;
![]() - имеет значения
от 0 до сотен. Если вещество свет не
поглощает
- имеет значения
от 0 до сотен. Если вещество свет не
поглощает
![]() ;
;
Теории Ми и Ганса могут быть использованы для оценки оптических свойств наполненных систем. Однако, для их применения в технике чаще всего не хватает данных по коэффициентам преломления, как действительной, так и мнимой части. Поскольку все пигменты являются кристаллическими веществами, у которых в разных направлениях кристаллических осей оптические показатели различны, измерить их на частицах порядка нанометра или микрометра трудно или невозможно.
Для описания оптических свойств пигментированных материалов в видимой области спектра применяют теорию двухпотокового приближения, согласно которой оптические свойства пигментированных материалов могут быть охарактеризованы двумя константами: коэффициентом поглощения К и коэффициентом рассеяния S (К и S имеют размерность L-1), показывающих ослабление падающего светового потока, отнесенного к единицы длины, за счет поглощения или рассеяния. Коэффициенты К и S не зависят от условий освещения и характеризуют только свойства самого элементарного объема.
Используя коэффициенты поглощения и рассеяния, Гуревич, Кубелка и Мунк рассмотрели оптические явления, происходящие в пленке (рисунок 6), и впервые предложили уравнение, описывающее поглощение и пропускание света образцами в зависимости от соотношения поглощения и рассеяния K/S .
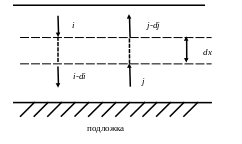
Рисунок 6 – Прохождение света через элементарный слой покрытия в соответствии с теорией ГКМ
Рассмотрим направленный вниз (падающий поток) и направленный вверх (отраженный поток).
Идущий вниз световой поток (интенсивность i) проходя сквозь пигментированный слой покрытия толщиной dx перпендикулярно к поверхности:
- уменьшается за счет поглощения на (-Kidx), где K - коэффициент поглощения;
- уменьшается за счет рассеяния на (-Sidx), где S - коэффициент рассеяния;
Навстречу световому потоку i идет поток j, отраженный от подложки, который:
- уменьшается за счет поглощения на (-Kjdx);
- уменьшается за счет рассеяния на (-Sjdx);
Следует отметить, что в теории Гуревича, Кубелки, Мунка коэффициент рассеяния учитывает не полное рассеяние света во всех направлениях, а только рассеяние в направлении, противоположном световому потоку. Поэтому световой поток, возникающий в результате рассеяния потока i, должен быть прибавлен к потоку j, а световой поток, получившийся за счет рассеяния потока j, - к потоку i. Таким образом, для изменения светового потока при прохождении через элементарный слой dx дифференциальное уравнение имеет вид:
![]()
или
![]()
Аналогично, изменение светового потока j:
![]()
При решении приведенных выше уравнений был введен коэффициент отражения ρ∞:
![]()
Коэффициент отражения для бесконечно толстой пленки, т.е. когда поток i не доходит до подложки и увеличение толщины которой уже не влияет на коэффициент отражения.
Связь коэффициента отражения с коэффициентами поглощения и рассеяния описывается формулой ГКМ [2-5]:
![]()
Двухпараметрическая теория рассеяния света не имеет принципиальных ограничений для применения в том или ином спектральном диапазоне. Ограничения теории ГКМ по существу состоят в следующем:
показатели поглощения К и рассеяния S должны быть постоянны по всей толщине слоя среды;
характер рассеяния должен быть независим от условий освещения и постоянен по всему объему среды [3,4].
Функция ГКМ лежит в основе расчета рецептур пигментированных материалов и широко используется для оптимизации состава пигментных паст на стадии диспергирования [2-5,17,18].
Оптимизация процесса диспергирования с использованием функции ГКМ
Известно, что оптическая эффективность пигментов в покрытии увеличивается с уменьшением размера частиц [2,18]. С ростом дисперсности пигментов увеличивается их укрывистость, красящая способность и чистота цвета.
Изменение красящей способности, выражаемое изменением значения функции Гуревича - Кубелки - Мунка F, описывается следующим уравнением [2,18]:
F = Кt - КFt/F∞
где К - константа скорости диспергирования;
t - продолжительность диспергирования;
F∞ - максимально достижимое значение функции Гуревича - Кубелки - Мунка, соответствующее бесконечно большой продолжительности диспергирования.
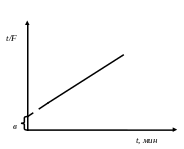
Эта зависимость может быть представлена в виде уравнения прямой (рисунок ):
t/F=t/F∞ +1/К.
|
По экспериментальным данным строят зависимость t/F=f(t) и аппроксимируют ее линейным уравнением:
y=ax+b.
|
Рисунок – Зависимость t/F от времени диспергирования |
|
Значение F∞ определяют как обратную величину углового коэффициента а или тангенса угла наклона прямой к оси абсцисс, и константу диспергирования К, как обратную величину сводного члена b или отрезка, отсекаемого на оси ординат:
![]() ;
;
![]() ;
;
Отношение максимально достижимого значения функции ГКМ к константе скорости диспергирования численно равно продолжительности диспергирования, необходимой для достижения половины предельного значения красящей способности. Это время, называемое сопротивлением диспергирования, является количественным критерием диспергируемости пигмента в тех или иных условиях.
![]() ;
;
Оптимальным временем диспергирования является время диспергирования, необходимое для достижения 0,9 F∞.[19].
При прочих равных условиях успешное диспергирование возможно только при правильном выборе соотношений пигмент : пленкообразователь и пленкообразователь : растворитель, т.е. при правильном выборе наполнения и концентрации пленкообразователя в растворе.
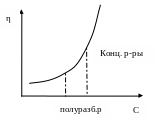
Рабочие концентрации пленкообразователя для диспергирования выбирают по зависимости вязкости или электрической проводимости его раствора от концентрации. Наиболее приемлемы для диспергирования концентрации пленкообразователя, которые соответствуют максимуму или началу выхода на плато на кривых зависимости электрической проводимости от концентрации, или на 2-3 % меньшие, чем концентрации, отвечающие подъему вязкости на реологических кривых [2,18].
Для определения оптимального для диспергирования содержания пигмента в пасте проводят диспергирование двух образцов, содержащих различное количество пигмента. Объемное содержание пигмента в образцах должно различаться примерно на 10 %. Верхний предел не должен превышать значение критического объемного содержания пигмента.
Используя значения констант скорости диспергирования, определенных для двух значений содержания пигмента в пасте при постоянной концентрации пленкообразователя, оптимальное для диспергирования содержание пигмента Спопт можно вычислить по следующей формуле:
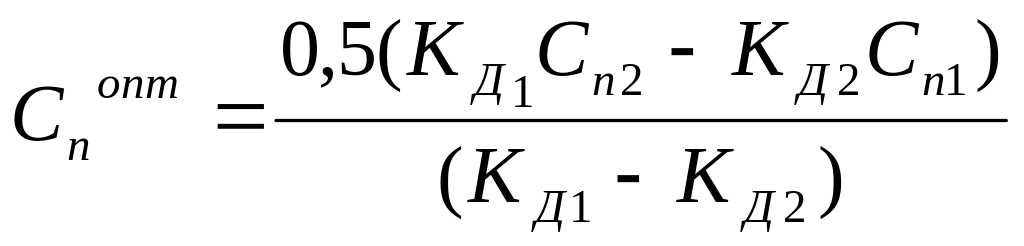 ;
;
где КД1,КД2 – константы скорости диспергирования для объемных содержаний пигмента в пасте Сп1,.Сп2.
При изменении концентрации пленкообразователя или изменении его состава в общем случае изменяется и значение оптимального для диспергирования объемного содержания пигмента. Однако в большинстве случаев при варьировании концентрации одного и того же пленкообразователя в области концентраций, лежащей левее начала структурирования, оптимальное объемное содержание пигмента меняется незначительно, оставаясь практически постоянным [18].
Влияние объемного содержания пигментов на оптические свойства композиционных материалов
Объемное содержание пигментов является одним из основных факторов, определяющих оптические, и, в том числе, колористические свойства композиционных покрытий. С увеличением объемного содержания пигментов в составе композиционных материалов до определенной величины оптическая плотность материалов увеличивается, при этом поглощение света преобладает над светорассеянием для материалов, поглощающих в видимой области. В результате этого при увеличении содержания пигментов наблюдается уменьшение светлоты для покрытий, наполненных различными пигментами, поглощающих в видимой области спектра.
Область критического наполнения соответствует переходу от матричного распределения частиц наполнителя или пигмента в объеме композиционного материала к контактному. В этой области частицы наполнителя или пигмента контактируют друг с другом через адсорбционные оболочки, а пространство между частицами заполнено полимером. Непрерывность полимерной фазы может сохраняться за счет адсорбционных оболочек. Именно в области критического наполнения наблюдается резкое изменение хода зависимостей большинства свойств наполненных композиционных материалов от содержания в них наполнителей или пигментов (изменяются реологические свойства лакокрасочных материалов, блеск, механические и защитные свойства покрытий) (рисунок 8) [2,22].
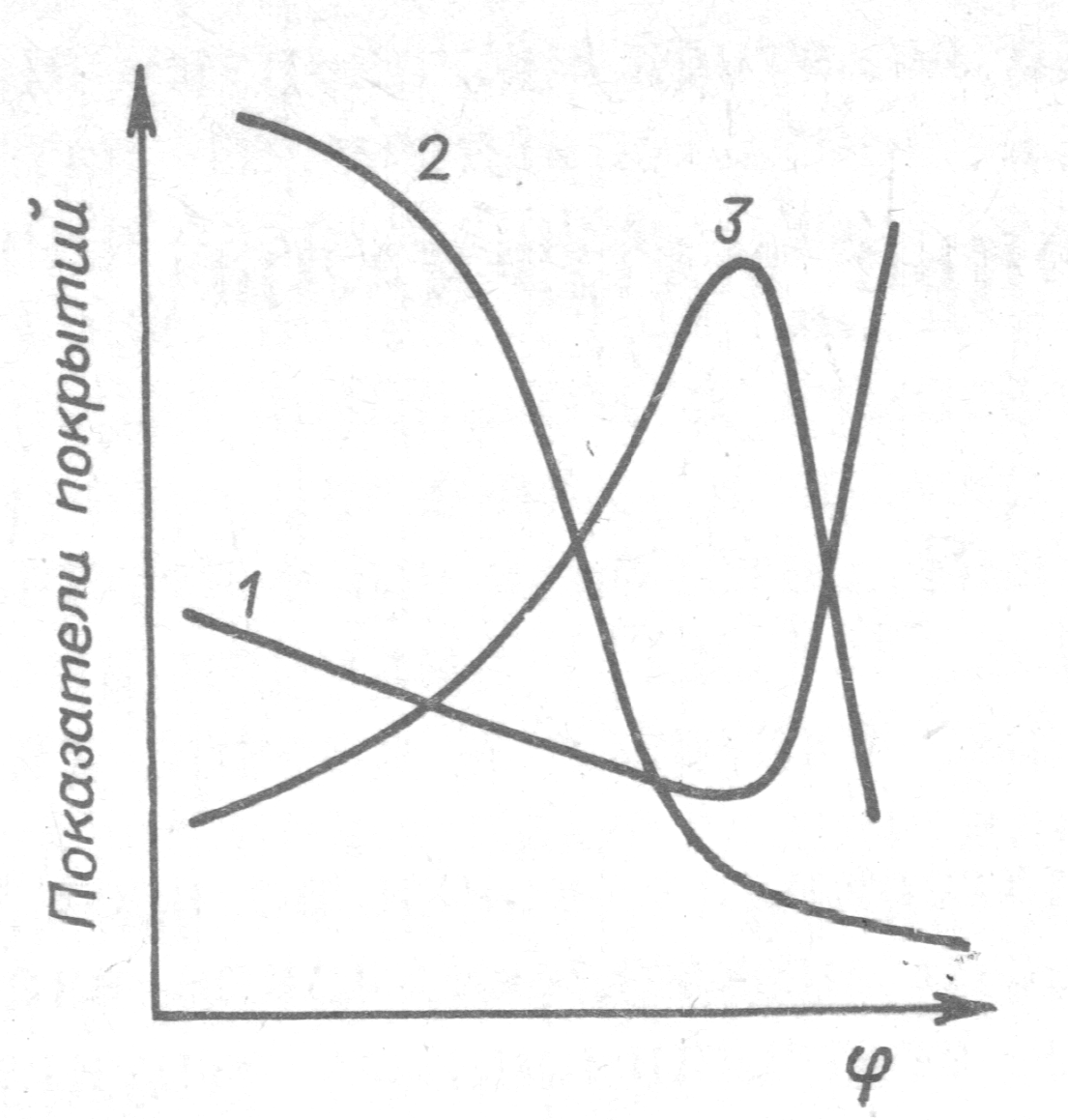
1 – паро и газопроницаемость, 2 – блеск, 3 – прочность при разрыве.
Рисунок 8 – Зависимость свойств пигментированных композиционных материалов от объемного содержания пигмента
Теоретически для сферических частиц, независимо от их диаметра, при наиболее плотной гексагональной упаковке φкр должно составлять 0,74 общего объема системы.
φкр=0,74 Vобщ;
Практически полидисперсные частицы упакованы не идеально плотно и φкр составляет обычно менее 0,55 общего объема.
В ряде лакокрасочных покрытий объемное содержание пигмента превышает критическое. К таким материалам относятся фасадные краски и краски для внутренней отделки помещений, у которых для обеспечения паропроницаемости покрытия необходима определенная пористость.
При повышении содержания пигмента выше критического обычно имеет место резкое возрастание укрывистости. В области, где объемная доля пигментов или наполнителей φ превышает ее критическое значение φкр, существенный вклад в совокупность свойств наполненных полимерных материалов вносит наличие в них пустот (воздуха), то есть пористость. При увеличении содержания наполнителя в их составе объемное наполнение растет вплоть до φкр. В закритической области оно остается практически постоянным, причем часть полимера замещается воздухом, т.е. материал становится пористым. Исходя из постоянства объемной доли наполнителя или пигмента в закритической области, Стигом введен индекс пористости, характеризующий объемную долю воздуха в промежутках между частицами.
Влияние дисперсного состава и формы частиц на оптические свойства пигментированных лакокрасочных материалов
Укрывистость, красящая способность цветных и разбеливающая способность белых пигментов, а также такие колористические показатели, как доминирующая длина волны (цветовой тон) и чистота цвета пигментов при неизменном химическом составе и кристаллической модификации зависит, прежде всего, от их дисперсности. Достаточно точное прогнозирование цвета на практике имеет ряд сложностей, связанных с тем, что спектр диффузного отражения в отличие от спектра пропускания зависит не только от положения и формы полосы поглощения, но и дисперсности пигментов, которая в значительной степени определяет характер рассеяния света.
Как следует из теории Релея и теории Ми, рассеяние света зависит от размера частиц. Согласно теории Ми, зависимость светорассеяния от размеров частиц выражается кривой с максимумом. Размер сферических частиц пигментов и наполнителей характеризуются диаметром, кубические (гранулированные пигменты)- длиной ребра куба, зернистые и игольчатые характеризуются наибольшим и наименьшим размерами, пластинчатые или чешуйчатые эквивалентным размером или диагональю.
Оптимальный с точки зрения укрывистости размер частиц белых пигментов (в нм) определяется уравнением Вебера:
![]() ;
;
λ – длина волны, нм;
n1 и n0 – коэффициенты преломления пигмента и связующего.
Из этого уравнения следует, что размер частиц пигментов, соответствующий максимальному рассеянию света в пигментированном покрытии и, соответственно, максимальной укрывистости, определяется соотношением показателей преломления связующего и пигмента [3].
Зависимость оптической эффективности хроматических пигментов от размера частиц можно представить следующим образом (рисунок 12) [28,29].
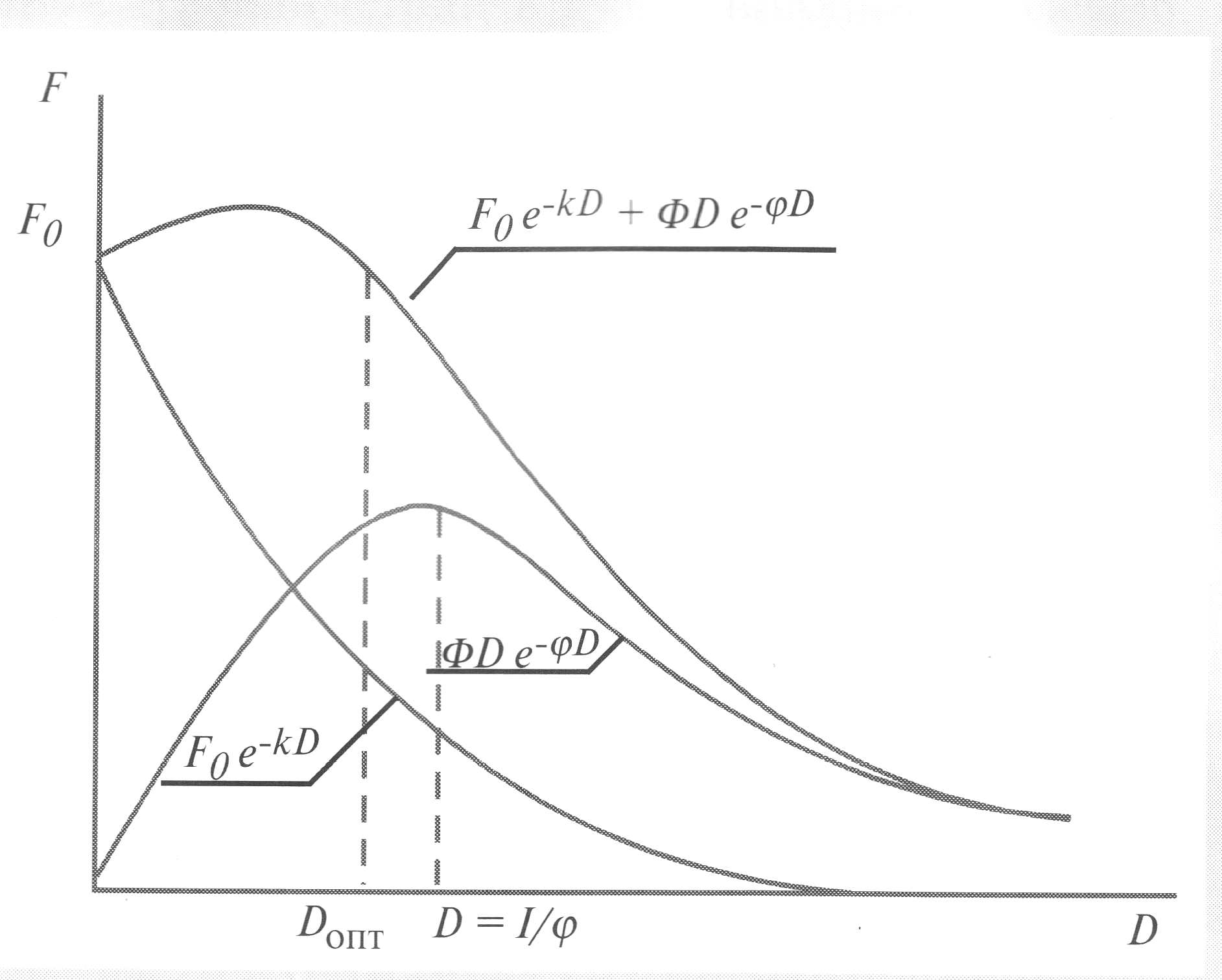
Рисунок 12 – Зависимость функции ГКМ хроматических пигментов от размера частиц как суперпозиция двух функций
С одной стороны, с ростом размера частиц экспоненциально уменьшается поглощение в максимуме абсорбции света и, соответственно, уменьшается значение функции ГКМ (F), начиная с F0. Эта зависимость описывается уравнением [29]
F = F0exp(-kD).
C другой стороны, имеет место экстремальное изменение зеркального отражения света от поверхности частиц в области «аномального» коэффициента преломления поглощающих свет частиц. Возникающее при этом диффузное отражение света, имеющего цвет дополнительный к поглощенному, повышает эффективную чистоту цвета. Эта завистмость подчиняется уравнению [29].
F1 = Dexp(-D);
где F1 можно считать виртуальным коэффициентом поглощения.
Таким образом, зависимость оптической эффективности хроматических пигментов от дисперсности может быть выражена уравнением:
F = F0 exp(-kD) + Dexp(-D);
где F0 – предельное значение функции ГКМ (для D 0);
к, Ф и - коэффициенты, имеющие размерность L-1.
В результате анализа этого уравнения и, учитывая нецелесообразность
повышения степени дисперсности выше значений, при которых скорость повышения интенсивности резко замедляется, получено [29] следующее уравнение для вычисления оптимального размера частиц:
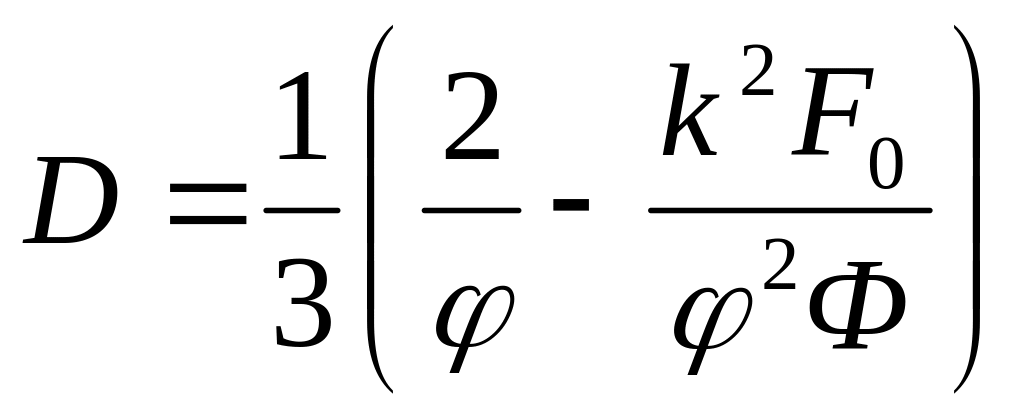 ;
;
Пренебрегая малыми величинами в высоких степенях, получаем, что положение максимума на кривой, описываемой зависимостью оптической эффективности хроматических пигментов от дисперсности, соответствует размеру частиц:
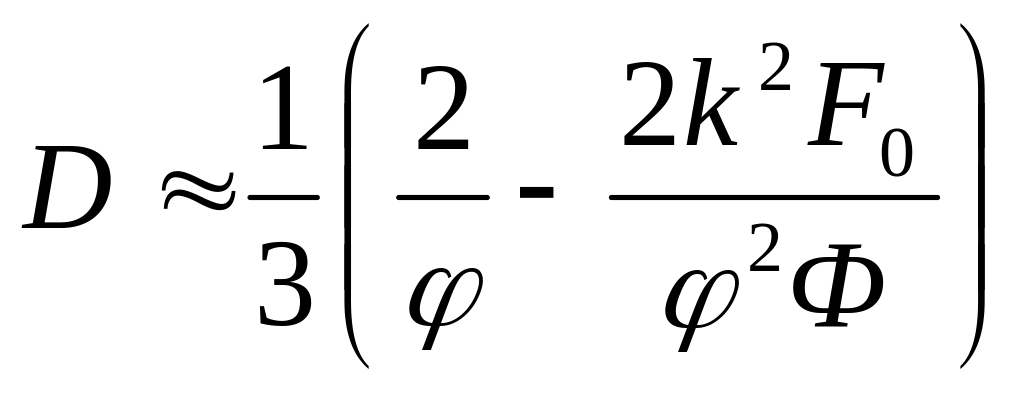 ;
;
Следует отметить, что максимума на зависимости оптической эффективности хроматических пигментов от дисперсности в области положительных значений может и не быть. Практически, это имеет место для многих пигментов. Максимуму функции F1 соответствует D = 1/. Этот размер, как отмечалось выше, подчиняется правилу Вебера. Таким образом, при условии, что – длина волны света, имеющего цвет, дополнительный к поглощенному, n1 и n0 - показатели преломления пигмента и среды для данной длины волны, соответственно, можно записать:
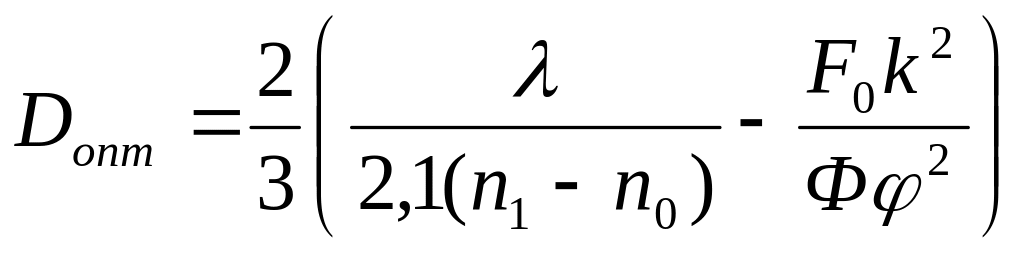 ;
;
Анализируя полученное уравнение видно, что оптимальный размер частиц хроматических пигментов равен двум третям размера частиц, соответствующих максимальному рассеянию света, за вычетом некоторой величины F0k2/Ф2. Практически, для всех пигментов коэффициент примерно в два раза больше к, откуда следует, что с достаточной степенью точности можно считать, что
![]() ;
;
Таким образом, чем выше коэффициент преломления пигмента на участке спектра, где пигмент имеет минимум поглощения света, и выше коэффициент поглощения на участке максимума поглощения, тем меньше оптимальный размер частиц хроматического пигмента.
Для большинства пигментов второй член уравнения уменьшает Dопт не более чем на 30%, а чаще всего на значительно меньшую величину, определяющуюся соотношением F0 и Ф. Поэтому для ориентировочных расчетов можно пользоваться упрощенной формулой:
![]() ;
;
Если известны показатели преломления среды и пигмента для участка спектра, соответствующего большему отражению или рассеянию, то, используя минимум экспериментальных данных, зависимость оптической эффективности от размера частиц приближенно может быть выражена уравнением [28,29]:
F
F0exp![]() + ФDexp
+ ФDexp![]() ;
;
Для максимума разбеливающей способности характерна узкая фракция размеров частиц, отвечающая оптимальному радиусу частицу rопт. Если rн<rопт, то пигмент имеет голубоватый оттенок, при rн>rопт – желтоватый [3].
На цвет пигментов влияет и форма частиц.
Изменение распределения частиц пигментов и наполнителей при формировании покрытий из наполненных композиционных материалов, происходящее вследствие флокуляции и коагуляции частиц также оказывает влияние на колористические характеристики покрытий.
Механизм зрения
В соответствии с современными представлениями восприятие того или иного цвета человеком происходит за счет воздействия лучистой энергии на
три типа фоторецепторов, чувствительных к красному, зеленому и синему свету, имеющихся в сетчатке глаза. Мозг воспринимает суммарный сигнал от рецепторов каждого типа как определенный цвет.
Наибольшее световое ощущение вызывает монохроматическое излучение с длиной волны 555 нм.
Непосредственно светочувствительными элементами являются зрительные рецепторы - палочки и колбочки. В сетчатке глаза имеется примерно 120 млн. палочек и 7 млн. колбочек.
В функциональном отношении палочки отвечают за скотопическое (ночное) зрение, т.е. за зрение при низких уровнях освещенности (менее 0,1 люкс). При высоких уровнях освещенности (свыше 500 люкс) палочки не работают, и цветовое зрение полностью обеспечивается колбочками. Это зрение называют фототропическим или дневным. Между этими двумя уровнями освещенности зрение обеспечивается и палочками и колбочками, такое зрение называют мезопическим или сумеречным зрением.
На рисунке 13 представлена кривые чувствительности человеческого глаза. Пики чувствительности колбочек лежат в синей (420 нм), зеленой (530 нм) и желто-зеленой (560 нм) областях спектра, в то время как длина волны пика чувствительности палочек расположена в 496 нм. Если построить спектры поглощения в зависимости от волнового числа (величины, обратной длине волны), то они будут иметь одинаковую форму и ширину полос.
Длина волны, нм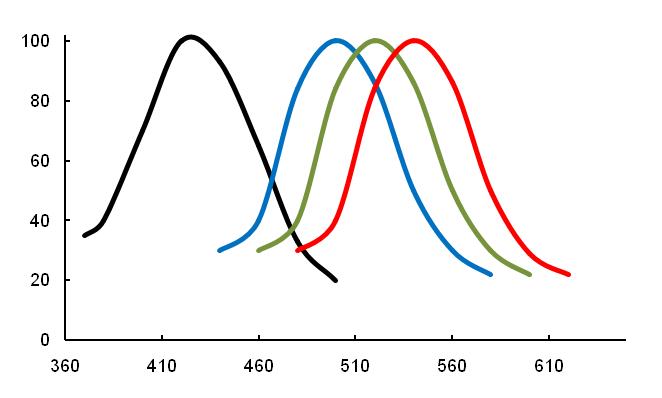
Максимум длины волны спектра поглощения:
Палочки:
родопсин, 419 нм;
Колбочки:
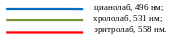
Рисунок– Кривые чувствительности фоторецепторов человеческого глаза
Любое изменение в спектре поглощения зрительных пигментов будет приводить к изменению дневной спектральной чувствительности зрительной системы. При отсутствии колбочек, чувствительных к длинноволновому излучению (протанопии), глаз воспринимает только средний и коротковолновый участок видимого спектра. Длина волны максимума чувствительности у протанопов сдвигается в сторону коротких длин волн.
Длина волны, нм
нормальный
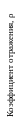
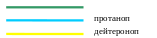
Рисунок - Смещения чувствительности глаза от чувствительности среднего наблюдателя
С другой стороны, кривая спектральной чувствительности для дейтеранопов складывается из спектров поглощения коротко- и длинноволновых колбочек.
Менее 0,01% всех людей страдают полной цветовой слепотой (монохроматы). Монохроматы различают только градации серого.
Нарушения цветового зрения гораздо чаще встречаются у мужчин, чем у женщин. Частота протаномалии у мужчин составляет примерно 0,9%, протанопии - 1,1%, дейтераномалии 3-4% и дейтеранопии - 1,5%. Тританомалия и тританопия встречаются крайне редко. У женщин дейтераномалия встречается с частотой 0,3%, а протаномалии - 0,5%.
Цвет пигментированных лакокрасочных материалов
В соответствии с ГОСТ Р 52489 – 2005 цвет - это свойство излучаемого, прошедшего через объект, рассеянного или отраженного света вызывать определенные зрительные ощущения в соответствии с его спектральным составом.
Электромагнитное излучение принято делить по частотным диапазонам (таблица 2). Между диапазонами нет резких переходов, они иногда перекрываются, а границы между ними условны [2-4,33].
Таблица 2 –Электромагнитные излучения
Название диапазона |
Длины волн, λ |
Источники |
Радиоволны: - сверхдлинные; - длинные; - средние; - короткие; - ультракороткие. |
более 10 км 10 км - 1 км 1 км - 100 м 100 м - 10 м 10 м - 2 мм |
Атмосферные явления. Переменные токи в проводниках и электронных потоках (колебательные контуры). |
Оптическое излучение: 1) Инфракрасное излучение: - коротковолновая область; - средневолновая область; - длинноволновая область 2) Видимое излучение
3) Ультрафиолетовое: - ближний диапазон; - дальний диапазон (вакуумный). |
0,74—2,5 мкм 2,5—50 мкм 50—2000 мкм 760-360 нм
380—200 нм 200-10 нм
|
Излучение молекул и атомов при тепловых и электрических воздействиях |
Излучение атомов под воздействием ускоренных электронов. |
||
Ионизирующее электромагнитное излучение: 1) Рентгеновское
2) Гамма излучение
|
0,005-10 нм
< 5×10−3 нм |
Радиоактивный распад, в результате комптон-эффекта гамма-излучения
Изомерный переход, ядерные реакции, синхротронное излучение |
Иногда, характеризуя выбранный участок спектра, пользуются не длиной волны, а частотой колебаний (в с-1) [3,4]:
![]() ;
;
где с = 3. 1010 см/с – скорость света в вакууме;
- длина волны, см.
Или обратной величиной длины волны (волновым числом, см-1).
В пределах видимого глазом излучения человек различает изменение длины волны как изменение цвета. Первые попытки классификации цветов были сделаны еще в Древней Греции.
Исаак Ньютон, изучавший солнечный свет и причины возникновения цветов, доказал, что существуют семь основных цветов, смешением которых можно получить все имеющиеся в природе оттенки. Это цвета спектра солнечного света: красный, оранжевый, желтый, зеленый, голубой, синий и фиолетовый.
Ньютон впервые ввел понятие цветовой модели, которая в дальнейшем получила название цветового круга Ньютона. Он использовал этот цветовой круг для систематизации многообразия цветов и определения цвета их смеси. В основу графического сложения цветов Ньютон положил правило нахождения центра тяжести [3-5].
На рисунке 15 представлен спектр разложения белого света, проходящего через призму [34].
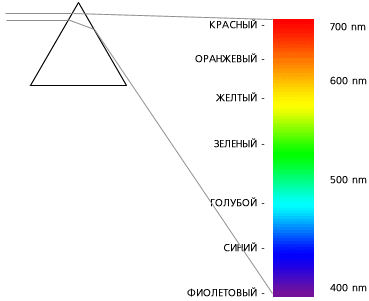
Рисунок 15 – Спектр, полученный при прохождении белого света через призму.
Задача оценки цвета не решается простым измерением распределения энергии излучения по спектру. По интервалу, занимаемому излучением, цвет можно указать вполне однозначно: если тело излучает или отражает в пределах 565- 580 нм, то цвет его всегда жёлтый. Однако обратное заключение верно не всегда - по известному цвету излучения невозможно уверенно указать его спектральный состав.
Если вещество поглощает какую-то часть спектра, то оно будет окрашено в цвет, дополнительный к поглощенному. Дополнительными называют цвета, способные при сложении давать белый цвет.
Причины окрашенности органических и неорганических соединений
Как известно, свет определенной длины волны (определенной частоты или, следовательно, определенной энергии) поглощается в том случае, если его энергия перехода соответствует энергии перехода электрона в более высокое энергетическое состояние. Частота электромагнитных колебаний, которые могут вызвать переход электрона с более низкого энергетического уровня на более высокий, определяется вторым квантовым уравнением Бора, так называемым частотным уравнением:
![]()
где Е1 – энергия атома в исходном состоянии;
Е2 – энергия атома в возбужденном состоянии;
h – постоянная Планка;
ν – частота.
В любом случае, для того чтобы соединение было окрашенным, необходимо наличие электронов в атоме, которые могут быть подняты на более высокий уровень таким образом, чтобы частота ν из второго квантового уравнения Бора соответствовала области видимого света. Электронные переходы, удовлетворяющие этому условию, могут иметь различный характер.
d-d переход.
Поскольку энергия видимого света сравнительно невелика, то, следовательно, необходимым условием окрашенности соединения является наличие так называемых рыхлосвязанных электронов. Как правило, легче возбуждаются электроны в ионах с незавершенной электронной оболочкой, т.е. в том случае, когда есть неспаренные электроны. Так почти все соединения элементов побочных подгрупп периодической системы, у которых валентность обычно не совпадает с номером группы, являются окрашенными. Иными словами, окрашенными обычно являются соединения элементов с незавершенными d - орбиталями.
Каждый электронный слой с главным квантовым числом 3 имеет набор из пяти d - орбиталей, отличающихся пространственным расположением (рисунок 16) [7,34].
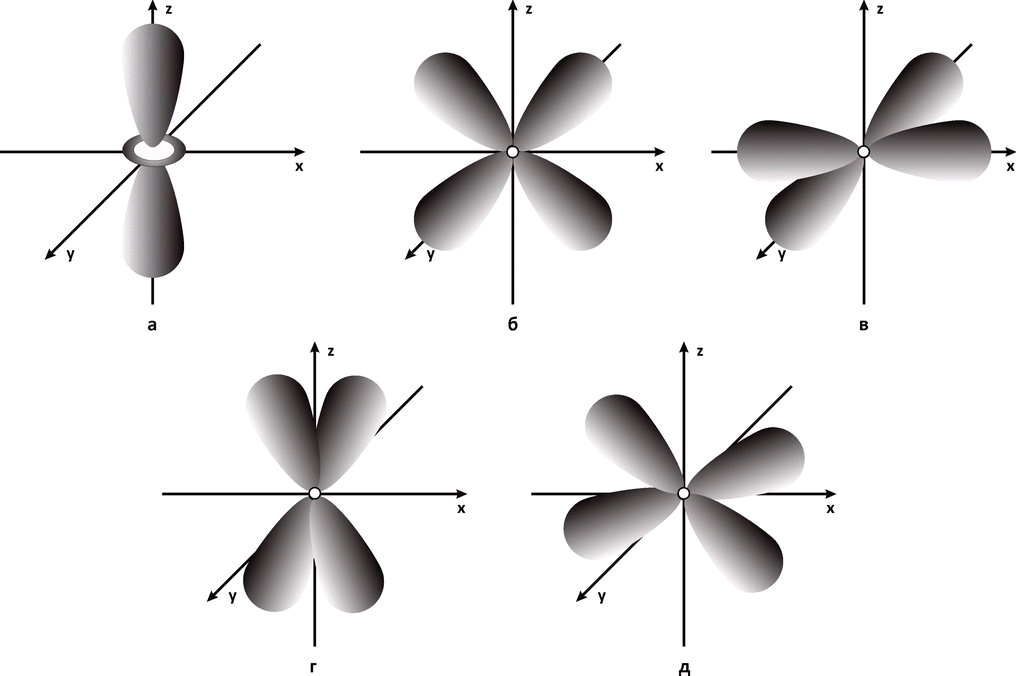
а - 3dz2-орбиталь; б - 3dxz-орбиталь; в - 3dx2y2-орбиталь; г - 3dyz-орбиталь; д - 3dху-орбиталь
Рисунок – Схемы пространственного расположения d - атомных орбиталей
Если катион d – элемента не находится в окружении заряженных групп, то все пять орбиталей энергетически эквивалентны. Таким образом, d – электрон может с одинаковой вероятностью находиться на любой из пяти орбиталей. Однако, если катион находится под влиянием электростатического поля отрицательных зарядов, окружающих его и расположенных в вершинах октаэдра, тетраэдра или занимающих в пространстве другие фиксированные положения, d – орбитали не будут энергетически эквивалентны. Наиболее энергетически выгодными будут орбитали, максимально удаленные от отрицательных зарядов, т.е. будет иметь место так называемое расщепление d – орбиталей в электростатическом кристаллическом поле на уровни разной энергии. Переход электрона с одного уровня на другой вследствие расщепления d – орбиталей в электростатическом кристаллическом поле носит название d – d перехода.
d – d Переходом обусловлена зеленая окраска оксида хрома (III) и изумрудной зелени, где ион Cr3+ имеет строение внешнего электронного слоя 3s23p63d3 и его основное состояние расщепляется в поле лигандов на три уровня. Таким переходом вызвана окраска медянки, где ион Cu2+ имеет строение внешнего электронного слоя 3s23p63d9 и его основное состояние расщепляется на два уровня. При синтезе диоксида титана предгидролизный раствор имеет интенсивную фиолетовую окраску, вызванную присутствием ионов [Ti(H2O)6]3+, где конфигурация внешнего электронного слоя у титана 3s23p63d1. Ион титана находится в октаэдрическом поле лигандов, и его d – орбиталь расщепляется на два уровня.
П3 – переход.
Второй причиной поглощения света является переход электрона в возбужденном состоянии с орбитали, почти полностью сконцентрированной у одного атома, на орбиталь, которая почти полностью принадлежит другому атому. Такой переход называют переходом с переносом заряда (ПЗ переход). Цвет многих кристаллических соединений обусловлен электронными переходами с молекулярных орбиталей, локализованных преимущественно на лигандах, на орбитали, локализованные на атоме металла. Данные переходы происходят под действием электромагнитных колебаний, соответствующих видимой части спектра. Этот переход обычно наиболее энергетически возможен, если кристаллическая решетка состоит из сильно поляризующих катионов и сильно поляризующих анионов. Для этого нужно, чтобы катионы имели небольшой ионный радиус и высокую валентность, а анионы – больший ионный радиус и низкую валентность. Увеличение поляризуемости аниона и поляризующей способности катиона приводит к снижению энергии, необходимой для осуществления перехода, т.е. сдвигает максимум поглощения света в длинноволновую область (батохромный эффект). Так, например, происходит углубление окраски при переходе от PbO к PbO2, вызванное уменьшением ионного радиуса свинца от 1,26 до 0,76 и возрастанием степени окисления свинца. Такое же явление наблюдается при переходе от Fe(OH)2 к Fe(OH)3 (ионные радиусы железа 0,8 и 0,67 соответственно). ПЗ – переходом обусловлена окраска таких важнейших групп хроматических пигментов, как крона (пигменты, в состав которых входит ион CrO42-) и железооксидные пигменты [2,7].