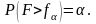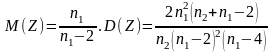- •1.Означення та приклади подій : випадкова, достовірна, неможлива, елементарна, складна.
- •2.Означення та приклад повної групи подій та простору елементарних подій.
- •3.Класичне означення ймовірності випадкової події
- •5.Дати означення відносної частоти появи події.
- •6. Дати геометричне та статистичне означення ймовірностей.
- •7.Дати визначення умовної ймовірності.
- •8.Формула множення ймовірностей для залежних та незалежних подій.
- •9.Формула для обчислення появи хоча б однієї події.
- •10. Формула повної ймовірності
- •11.Формула Баєса.
- •13.Формула Бернуллі для обчислення ймовірностей,умова використання. Наслідки.
- •14. Найімовірніше число наступів події в схемі Бернуллі.
- •15.Сформулювати локальну теорему Мауавра-Лапласа.
- •16.Сформулювати інтегральну теорему Мауавра-Лапласа.
- •17.Функція Гаусса та її властивості
- •18.Функція Лапласа та її властивості.
- •19.Формула Пуассона,умови її використання.
- •20.Означення випадкової величини, дискретної та неперервної випадкової величини.
- •21.Закон розподілу випадкової величини.
- •22.Інтегральна функція розподілу випадкової величини: означення.Властивості.
- •30.Означення закону розподілу багатовимірної випадкової величини.
- •32. Коефіцієнт кореляції та його властивості
- •Щільність імовірностей системи п випадкових величин є функція
- •34.Двовимірний нормальний закон.
- •35.Біномінальний закон розподілу двв, числові характеристики.
- •36. Пуасонівський закон розподілу двв, числові характеристики.
- •37.Геометрический закон розподілу двв, числові характеристики.
- •38. Гіпергеометричний закон розподілу двв, числові характеристики.
- •39.Рівномірний закон розподілу.
- •40. . Нормальний закон розподілу
- •41.Показниковий закон та його використання в теорії надійності та теорії черг.
- •43. Правило трьох сигм. Логарифмічний нормальний закон розподілу
- •45. Теорема Чебишова
- •46. ) Теорема Бернулі
- •48.Предмет і задачі математичної статистики.
- •49. Утворення вибірки. Генеральна та вибіркова сукупність.
- •50. Статистичним розподілом вибірки
- •51.Емпірична функція розподілу, гістограма та полігон.
- •52.Числові характеристики : вибіркова середня, дисперсія вибірки, середньоквадратичне відхилення.
- •53.Мода й медіана,емпіричні початкові та центральні моменти, асиметрія та ексцес.
- •54.Дати визначення статистичної оцінки.
- •55.Точкові та інтервальні статистичні оцінки.
- •56.Дати визначення довірчого інтервалу.
- •57.Що таке нульова та альтернативна статистичні гіпотези.
- •58.Перевірки правдивості нульової гіпотези про нормальний закон розподілу ознаки генеральної сукупності.
- •59.Емпіричні та теоретичні частоти.
- •60.Критерії узгодження Пірсона та Колмогорова.
- •61.Помилки 1-го і 2-го роду.
- •62.Статистичний критерій.Критична область.
- •63.Дати означення моделі експерименту.
- •64.Дати поняття одно фактичний аналіз.
- •65.Що таке таблиця результатів.
- •66.Загальна дисперсія,між групова та внутрішньо групова дисперсія.
- •67.Загальний метод перевірки впливу фактора на ознаку способом порівняння дисперсії.
- •68.Поняття про функціональна ,статистична і кореляційна залежності.
- •70. Вибірковий коефіцієнт кореляції
- •71. Множина регресії ,множинний коєфіцієнт кореляції та його властивості .
38. Гіпергеометричний закон розподілу двв, числові характеристики.
Гіпергеометричний закон розподілу має випадкова величина X , якщо вона набуває
послідовні невід’ємні цілі значення, а відповідні ймовірності знаходяться за формулою
P
(X=k)=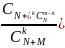
де K,m,N,M – невід’ємні цілі числа.
39.Рівномірний закон розподілу.
Якщо ймовірність потрапляння випадкової величини на інтервал пропорційна до довжини інтервалу і не залежить від розташування інтервалу на осі, то вона має рівномірний закон розподілу. Щільність такого розподілу:
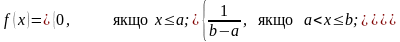
Рівномірний закон розподілу легко моделювати. За допомогою функціональних перетворень із величин, розподілених рівномірно, можна діставати величини з довільним законом розподілу. Числові характеристики розподілу:
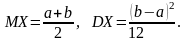
40. . Нормальний закон розподілу
задається
щільністю

Параметри
 ,
які входять до виразу щільності розподілу,
є відповідно математичним сподіванням
та середнім квадратичним відхиленням
випадкової величини. Нормальний
закон розподілу широко застосовується
в математичній статистиці. Для обчислення
ймовірності потрапляння випадкової
величини, розподіленої нормально, на
проміжок використовується функція
Лапласа:
,
які входять до виразу щільності розподілу,
є відповідно математичним сподіванням
та середнім квадратичним відхиленням
випадкової величини. Нормальний
закон розподілу широко застосовується
в математичній статистиці. Для обчислення
ймовірності потрапляння випадкової
величини, розподіленої нормально, на
проміжок використовується функція
Лапласа:
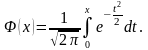
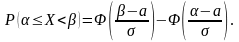
Часто застосовується також формула:
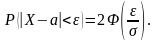
41.Показниковий закон та його використання в теорії надійності та теорії черг.
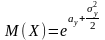 .
.
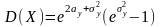 .
.
Щільність розподілу випадкової величини, розподіленої за показниковим законом, задається формулою:
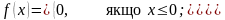
Випадкові величини з таким законом розподілу широко застосовуються в задачах з теорії надійності та теорії масового обслуговування. Числові характеристики:
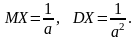
Ме=ln2/a.
Серед усіх законів неперервних випадкових величин лише експоненціальному притаманна властивість – відсутність післядії, а саме: якщо пов”язати випадкову величину із часом, то для цього закону минуле не впливає на передбачення подій у майбутньому. Цю властивість закону використовують у харківських випадкових процесах, теорії масового обслуговування, теорії надійності.
42.
Розподіл
Стьюдента.
Розподіл Стьюдента з n
cтупенями волі має випадкова величина
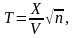 де Х
— нормально розподілена величина з
нульовим математичним сподіванням і
одиничною дисперсією, а
де Х
— нормально розподілена величина з
нульовим математичним сподіванням і
одиничною дисперсією, а
 .
Випадкова величина
.
Випадкова величина
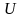 не залежить від Х
і має розподіл
не залежить від Х
і має розподіл
 з
n
ступенями волі. Щільність розподілу
з
n
ступенями волі. Щільність розподілу
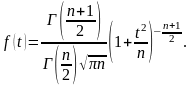 Графік щільності розподілу Стьюдента
за зовнішнім виглядом нагадує нормальні
криві. Але вони значно повільніше
спадають до осі t,
якщо
Графік щільності розподілу Стьюдента
за зовнішнім виглядом нагадує нормальні
криві. Але вони значно повільніше
спадають до осі t,
якщо
 особливо
за малих значень n
особливо
за малих значень n
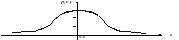
Складено
таблиці розподілу Стьюдента, здебільшого
виду
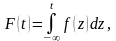 для кількості ступенів волі від 1 до 20.
Якщо кількість ступенів волі більша,
то можна застосовувати нормальний закон
розподілу з нульовим математичним
сподіванням і одиничною дисперсією.
для кількості ступенів волі від 1 до 20.
Якщо кількість ступенів волі більша,
то можна застосовувати нормальний закон
розподілу з нульовим математичним
сподіванням і одиничною дисперсією.
M(Z)=0.
 .
.
Розподіл
Фішера.
Якщо випадкові величини
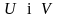 незалежні і мають
— розподіл відповідно з
незалежні і мають
— розподіл відповідно з
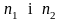 ступенями волі, то випадкова величина
ступенями волі, то випадкова величина
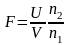 має розподіл Фішера з
має розподіл Фішера з
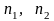 ступенями волі. Щільність цього розподілу
подається формулою:
ступенями волі. Щільність цього розподілу
подається формулою:
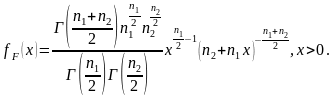 Щільність
розподілу Фішера має графік, зображений
на
Щільність
розподілу Фішера має графік, зображений
на
 Для
розподілу Фішера складено таблиці, в
яких для відповідної кількості ступенів
волі для ймовірностей
Для
розподілу Фішера складено таблиці, в
яких для відповідної кількості ступенів
волі для ймовірностей
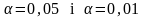 наведено значення
наведено значення
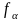 –
–