13.Формула Бернуллі для обчислення ймовірностей,умова використання. Наслідки.

Імовірність того, що в n незалежних випробуваннях, у кожному з яких імовірність Р(А) = р, подія А відбудеться m раз, подається так:

Формула застосовується, якщо

Імовірність того, що в результаті n незалежних експериментів подія А з’явиться від mi до mj раз, обчислюється так:

Умови використання. Якщо відбувається декілька випробувань, причому ймовірність події А в кожному з випробувань не залежить від результатів інших випробувань, то такі випробування називають незалежними відносно події А.

В різних незалежних випробуваннях подія А може мати або різні ймовірності, або одну й ту ж саму ймовірність. Будемо розглядати тільки варіант зі сталою ймовірністю.

Нехай відбувається n незалежних випробувань, в кожному з яких подія А може з'явитися або не з'явитися. Домовимося вважати, що ймовірність події А в кожному з випробувань стала, а саме дорівнює p. Тоді, ймовірність ненастання події А в кожному з випробувань також стала і дорівнює q = 1 - p.

Поставимо собі задачу обчислити ймовірність того, що при n випробуваннях подія А відбудеться рівно k разів і, відповідно, не відбудеться n - k разів. Важливо підкреслити, що не вимагається, щоб подія А повторилась рівно k разів в певній послідовності.

Поставлену задачу можно вирішити за допомогою формули Бернулі.

14. Найімовірніше число наступів події в схемі Бернуллі.

Якщо проводиться n незалежних випробувань, в кожному з яких ймовірність появи події А одна і та ж і дорівнює p, то ймовірність того, що подія А з'явиться в цих n випробуваннях m раз, виражається формула Бернуллі

P_n(m) = Cⁿ_k·p^m·q^n-m, де q = 1-p. Число m₀ називається найімовірнішим числом  наступів події А в n випробуваннях і одно цілої частини числа (n+1)p, а при цілому (n+1)p найбільше значення досягається при двох номерах: m₁=(n+1)p-1 і m₂=(n+1)p.  Якщо р≠0 і р≠1, число m₀ можна визначити з подвійного нерівності

np-q ≤ m₀ ≤ np+p.

15.Сформулювати локальну теорему Мауавра-Лапласа.

Імовірність того, що в n незалежних випробуваннях, у кожному з яких Р(А) = р, подія А відбудеться m раз, подається такою наближеною залежністю:

Локальна теорема Лапласа дає змогу обчислювати ймовірності ,

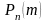якщо n > 10 i p > 0,1.

16.Сформулювати інтегральну теорему Мауавра-Лапласа.

Імовірність того, що подія А відбудеться від до 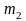раз при проведенні n незалежних випробувань, у кожному з яких подія А відбувається з імовірністю р, подається формулою:

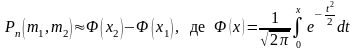—функція Лапласа;

Значення функції Лапласа наводяться у спеціальних таблицях.

17.Функція Гаусса та її властивості

У математиці функцією Гауса (названа за іменем Карла Фрідріха Гауса) є функція, що виражається залежністю

для дійсних чисел константа a > 0, b, c > 0, і e ≈ 2.718281828 (Число Ейлера).

Властивості. Ґаусова функція є такою, що її логарифм дає квадратичну фунцію.

Через параметр c можна виразити ширину піку (FWHM) на половині його висоти згідно з формулою: 

Гаусова функція є аналітичною, і її границя при x→±∞ є 0.

Визначений інтеграл від ґаусової функції дає функцію помилок

Визначений інтеграл з нескінченними границями має властивість

Цей інтеграл рівний 1 тоді і тільки тоді, коли a = 1/(c√(2π)), і в цьому випадку Гаусіан є щільністю нормального розподілу випадкової величини з математичним очікуванням μ=b і дисперсією σ²=c².

При перетворенні Фур'є функції Гауса з параметрами a, b=0 і c отримуємо іншу функцію Гауса, з параметрами ac, b=0 і 1/c. Отже, як частковий випадок, функція Гауса з b=0 і c=1 є інваріантом щодо перетворення Фур'є