60.Критерії узгодження Пірсона та Колмогорова.

Критерій узгодженості Пірсона - один з найвідоміших критеріїв  , тому його часто і називають просто "критерій хі-квадрат". Використовується для перевірки гіпотези про закон розподілу.

Ґрунтується на групованих даних. Область значень передбачуваного розподілу   ділять на деяке число інтервалів. Після чого будують функцію відхилення ρ по різницях теоретичних імовірностей попадання в інтервали групування й емпіричних частот.

Нехай X=(X₁,…, X_n) — вибірка з розподілу  . Перевіряється проста гіпотеза   проти складної альтернативи  . Нехай A₁,…, A_k — інтервали групування в області значень випадкової величини з розподілом  . Позначимо для j=1,…,k через   число елементів вибірки, що потрапили в інтервал  : ,

і через   — теоретичну ймовірність   попадання в інтервал   випадкової величини з розподілом  . З необхідністю,  . Як правило, довжини інтервалів вибирають так, щоб 

   

У статистиці критерій узгодженості Колмогорова (також відомий, як критерій узгодженості Колмогорова — Смирнова) використовується для того, щоб визначити, чи підпорядковуються два емпіричних розподіли одному закону, або визначити, чи підпорядковується емпіричний розподіл певній моделі.

Критерій Колмогорова виглядає так:  .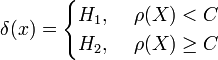

61.Помилки 1-го і 2-го роду.

Похибки першого роду  і похибки другого роду  в математичній статистиці — це ключові поняття завдань перевірки статистичних гіпотез

Нехай дано вибірку   з невідомого розподілу  , і поставлена бінарна задача перевірки статистичних гіпотез: Н0 Н1

де   — нульова гіпотеза, а   — альтернативна гіпотеза. Припустимо, що заданий статистичний критерій

,

що зіставляє кожній реалізації вибірки   одну з гіпотез, які маємо. Тоді можливі чотири ситуації:

1. Розподіл   вибірки 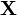  відповідає гіпотезі Н0, і вона точно визначена статистичним критерієм, тобто  .

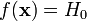2. Розподіл   вибірки   відповідає гіпотезі Н0, але вона невірно знехтувана статистичним критерієм, тобто  .

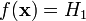3. Розподіл   вибірки   відповідає гіпотезі  , і вона точно визначена статистичним критерієм, тобто  .

4. Розподіл   вибірки   відповідає гіпотезі  , але вона невірно знехтувана статистичним критерієм, тобто  .

У другому і четвертому випадку говорять, що відбулася статистична помилка, і її називають похибкою першого і другого роду відповідно.

62.Статистичний критерій.Критична область.

Статистичний критерій — строге математичне правило, за яким приймається або відкидається та або інша статистична гіпотеза. Побудовою критерію є вибір відповідної функції від результатів спостережень (ряду емпірично набутих значень ознаки), яка служить для виявлення міри розбіжності між емпіричними значеннями і гіпотетичними.

Нехай дано вибірку   з невідомо сумісного розподілу  , і сім'я статистичних гіпотез  . Тоді статистичним критерієм називається функція, що встановлює відповідність між величинами, що спостерігаються, і можливими гіпотезами:

.

Таким чином кожній реалізації вибірки   статистичний критерій зіставляє найбільш підходящу з точки зору цього критерію гіпотезу про розподіл, що породив дану реалізацію.

Значення статистичного критерію підмножини А Î  , при яких нульова гіпотеза приймається, називається областю прийняття гіпотези, а підмножина значень Ā, при яких гіпотеза Н₀ відхиляється – критичною областю.