56.Дати визначення довірчого інтервалу.

Довірчий інтервал — інтервал, у межах якого з заданою довірчою імовірністю можна чекати значення оцінюваної (шуканої) випадкової величини. Застосовується для повнішої оцінки точності в порівнянні з точковою оцінкою.

Інтервал називається довірчим інтервалом, а імовірність – довірчою імовірністю або надійністю , що відповідає даному довірчому інтервалу

57.Що таке нульова та альтернативна статистичні гіпотези.

Нульовою (основною) гіпотезою H0 називають висунуту гіпотезу.

Альтернативною (конкуруючою) гіпотезою Hi називають про­тилежну до нульової гіпотезу.

Висовувану статистичну гіпотезу називають нульовою (нуль-гіпотезою) і позначають Н0. Часто для стислості нуль-гіпотезу формулюють так: відмінностей немає, а ті, що спостерігаються, випадкові. 

Протилежну гіпотезу, тобто припущення про те, що відмінності не випадкові називають альтернативною і позначають Нa. У загальному випадку альтернативних гіпотез може бути декілька.

Рішення про відхилення чи визнання статистичної гіпотези проводять на основі дослідних даних, які супроводжуються випадковими помилками. Тому не виключена можливість помилки також при прийнятті рішення, причому можливі два варіант помилкових рішень:

1. може бути відхилена, у дійсності вірна, нуль-гіпотеза — це помилка першого роду;

2. може бути визнана, у дійсності невірна, нуль-гіпотеза — це помилка другого роду.

58.Перевірки правдивості нульової гіпотези про нормальний закон розподілу ознаки генеральної сукупності.

Найбільш розповсюдженим критерієм перевірки гіпотези Н₀ про закон розподілу ознаки генеральної сукупності є критерій узгодженості:

де m – число інтервалів, на які розбита вибірка, n – об’єм вибірки, n_i – частота і-го інтервалу, r_і – ймовірність попадання значень ознаки в і-ий інтервал, яка обчислюється для теоретичного закону розподілу.

Спостережуваним значенням К_сп називається значення критерію, обчислене по результатах вибірки.

59.Емпіричні та теоретичні частоти.

Зазвичай емпіричні і теоретичні частоти розрізняються в силу того, що:

• розбіжність випадково і пов'язане з обмеженою кількістю спостережень;

• розбіжність невипадково і пояснюється тим, що статистична гіпотеза про те, що генеральна сукупність розподілена нормально - помилкова.

Таким чином, критерії згоди дозволяють спростувати або підтвердити правильність висунутої при вирівнюванні ряду гіпотези про характер розподілу в емпіричного ряду.

Емпіричні частоти отримують в результаті спостереження. Теоретичні частотирозраховують за формулами. Для закону нормального розподілу їх можна знайти наступним чином:

  

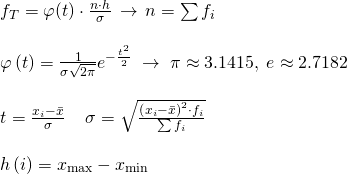
Σƒ_i—сума накопичених (кумулятивних) емпіричних частот

h - різниця між двома сусідніми варіантами

σ - вибіркове середньоквадратичне відхилення

t-нормоване (стандартизоване відхилення)

φ(t)-функція щільності ймовірності нормального розподілу (знаходять по таблиці значень локальної функції Лапласа для відповідного значення t)