48.Предмет і задачі математичної статистики.

 Предмет   математичної   статистики  - це формальна математична сторона статистичних методів дослідження, байдужа до специфічної природи об'єктів, які вивчаються. Згідно з цим визначенням  предмет   математичної   статистики  є чисто математичною теорією математико-статистичних методів незалежно від специфіки  і  сфери їх застосування.

Всі задачі математичної статистики умовно можна розчленити на дві групи.

Першою з них є розробка методів збору і групування статистичних даних, отриманих в результаті спостережень, опрацювання статистичних звітів чи даних в результаті спеціально поставлених експериментів.

Друга задача полягає в розробці методів аналізу статистичних даних залежно від мети. Сюди належать:

а) оцінка ймовірності події; знаходження функції розподілу випадкової величини; оцінка залежності випадкової величини від інших випадкових величин, тощо; оцінка невідомих параметрів розподілу;

б) перевірка статистичних гіпотез про зроблені вище припущення.

Висновки за допомогою методів математичної статистики, зроблені зі зібраних статистичних даних, повинні правильно відображати загальні ймовірносні характеристики процесу, що досліджується.

49. Утворення вибірки. Генеральна та вибіркова сукупність.

два способи можливого утворення вибірки:

з повторенням, коли елемент після вивчення повертається назад до сукупності, що вивчається та може бути повторно вивчений;

без повторення, коли елемент після вивчення назад до сукупності не повертається.

На практиці статистичних досліджень відрізняють два види дослідів:

• суцільний, коли розглядаються всі елементи сукупності

• вибірковий, де вивчається лише деяка частина елементів.

     Вся сукупність елементів, яку треба вивчити називається генеральною сукупністю. Поняття генеральної сукупності, в певному сенсі, є аналогічним поняттю випадкової величини (закону розподілу ймовірностей), бо повністю обумовлене певним комплексом умов.      Та частина об’єктів, що її відібрано для безпосереднього вивчення із генеральної сукупності, називається вибірковою сукупністю (або просто – вибіркою). Кількість елементів у генеральній чи вибірковій сукупності називають їх об’ємами.

     Вибіркова сукупність розглядається, як деякий емпіричний аналог генеральної сукупності. Сутність вибіркового методу полягає в тому, щоб за деякою частиною генеральної сукупності(за вибіркою) робити висновки про її властивості вцілому, наприклад, про її закон розподілу, або про числові значення її певних параметрів. Головним недоліком вибіркового методу є помилки досліду, які також називають помилками репрезентативності.

50. Статистичним розподілом вибірки

називається таблиця, в якій вказані значення х ознаки Х у зростаючому порядку (в цьому випадку значення утворюють дискретний варіаційний ряд, самі значення ознаки називаються варіантами), а також відповідні частоти або відносні частоти

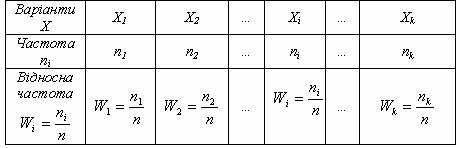
де n=n₁+n₂+…n_k,  , якщо i>j,  ;

51.Емпірична функція розподілу, гістограма та полігон.

Емпіричною функцією розподілу F_n(x) називається відносна частота (частість) того, що ознака (випадкова величина Х) прийме значення, менше ніж заданий х, тобто

F_n(x)=w(X<x)= 

Іншими словами емпірична функція розподілу являє собою нагромаджену частість  =

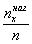
Можна помітити, що статистичний ряд – це статистичний аналог розподілу ознаки (випадкової величини Х). В цьому сенсі полігон (гістограма) – аналог кривої розподілу, а емпірична функція розподілу - функції розподілу випадкової величини Х.

Полігон, як правило, використовують для зображення дискретного статистичного ряду, він являє собою ламану, для якої кінці відрізків мають координати (x_i,n_i).

Гістограму використовують для зображення лише неперервних статистичних рядів (вона являє собою ступінчасту фігуру із прямокутників з основами, що дорівнюють значенням ознаки k_i=x_i+1–x_i, та висотами, що дорівнюють частотам (частостям) n_і (w_i) інтервалів). Якщо з’єднати середини верхніх сторін відрізками, то отримаємо полігон того ж самого розподілу.