1.Означення та приклади подій : випадкова, достовірна, неможлива, елементарна, складна.

Достовірна подія обов’язково настає, неможлива подія обов’язково не настає, а випадкова подія настає, або не настає, у результаті експерименту.

Подія називається випадковою ,якщо в результаті експерименту вона може настати або настати залежно від дії численних дрібних факторів.

Приклад: Монету підкидають один раз,поява герба-подія випадкова.

Елементарні події — наслідки випадкового експерименту, з яких під час експерименту відбувається рівно один. Приклади простору наслідків експеримента,   — елементарних подій:

 (Якщо об'єкти злічені, а простір наслідків — натуральні числа, елементарними подіями є будь-які множини  , де  .)

Випадкова подія наз. складною, якщо її можно розкласти на прості події.

2.Означення та приклад повної групи подій та простору елементарних подій.

Повною групою подій у теорії ймовірності називається система випадкових подій така, що в результаті проведеного випадкового експерименту неодмінно станеться одне з них.

Хай   є імовірнісний простір. Будь-яке розбиття простору елементарних подій   називається повною групою подій.

Повна група подій зазвичай використовується в формулі повної ймовірності.

Нехай, проводиться підкидання монети. В результаті цього експерименту обов'язково станеться одна з наступних подій:

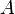• : монета впаде орлом;

• : монета впаде решкою;

Події, які в реальному житті не можуть відбутися, ми не розглядаємо. Наприклад:

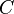• : монета впаде на ребро;

• : монета зависне в повітрі.

Таким чином, система   є повною групою подій.

Простір елементарних подій — множина всіх можливих наслідків стохастичного експерименту. Тобто, множина елементарних подій. Зазвичай позначаєтеся літерою Ω, також S або U.

Простір елементарних подій називається дискретним, якщо множина Ω скінченна або зліченна.

Довільна підмножина простору елементарних подій є подією, всі вони утворюють алгебру подій.

Припустимо, що монету підкидають один раз. Простір елементарних подій, цього експерименту має вигляд Ω = {Г, Р}, де Г означає появу герба, буква Р — появу решки. Монету підкидають двічі. Простором елементарних подій цього експерименту є множина Ω = {ГГ, ГР, РГ, РР}. Тут ГР означає, наприклад, що при першому підкиданні з'явився герб, а при другому — решка.

Підкидають шестигранний гральний кубик на якому вибиті очки від 1 до 6. Нас цікавить число очок, яке випало. Простором елементарних подій тут може бути Ω = {1,2,3,4,5,6}.

3.Класичне означення ймовірності випадкової події

Умовність випадкової події А наз. невід’ємне число Р(А), що дорівнює відношенню числа елементарних подій m (0<=m<=n) ,які сприяють появі А, до кількості всіх елементарних подій n простору Ω .

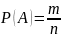
Для неможливої події - Р(ɸ)=0 (m=0)

Для вірогідної події - Р(Y)=1 (m=n)

Для довільної випадкової події 0<P(A)<1

4.Дати означення та вказати властивості перестановки,сполучення, комбінації елементів.

I. Перестановки

Нехай є множина М, яка складається із n елементів: а_1, a₂, а₃,…, а_n. Якщо переставляти ці елементи можливими способами, залишаючи незмінним їх загальне число, одержуємо декілька послідовностей: а₁, а₂, а₃,…,а_n,…,а_n-1,а_n-2,…, а₁ і т. д. Кожна з таких послідовностей є перестановкою із даних n елементів.

Перестановкою (the permutation) із n елементів називається будь-яка скінченна послідовність (progression), яка одержується в результаті упорядкування деякої скінченної множини, складеної з nелементів. Число всіх перестановок із n елементів позначається Р_n. Це число дорівнює добутку всіх цілих чисел від 1 до n. Позначають:

.

II Сполучення (комбінації)

Нехай є множина М, яка складається з n різних елементів. Будь-яка підмножина множини М, яка містить kелементів (k=0, 1, 2, ..., n), називається сполученням (combination) або комбінацією з даних n елементів по k елементів, якщо ці підмножини відрізняються хоча б одним елементом. Число різних сполучень із nелементів по k позначається   .Іноді замість   пишуть ( ).

Формулу для  можна записати в іншому вигляді. Помноживши чисельник i знаменник дробу в правій частині на добуток  , одержуємо:

.

III Розміщення

Кожна впорядкована підмножина, яка містить k елементів даної множини з n елементів, називаєтьсярозміщенням (accommodation) із n по k елементів. Таким чином, два різних розміщення із даних n елементів по k відрізняються один від одного або складом елементів, або порядком їх розміщення.