
7 Билет:
Теорема
об арифметических операциях с пределами:
пусть
 сходящиеся
последовательности: тогда
сходящиеся
последовательности: тогда
 тоже сходится,
причем
тоже сходится,
причем

Доказательство:
пусть
 тогда
в силу теореме об общем виде сходящихся
последовательностей
тогда
в силу теореме об общем виде сходящихся
последовательностей

Тогда
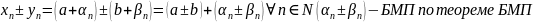
Итак представили в виде суммы числа и БМП
значит
сходящаяся и
представили в виде суммы числа и БМП
значит
сходящаяся и

2) тоже
сходящиеся, причем
тоже
сходящиеся, причем
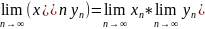
Доказательсто:
по теореме
о БМП

 БМП как произведение
огр. Последовательности на БМП ( по
теореме о БМП)
)-
БМП ( по теореме о БМП)
БМП как произведение
огр. Последовательности на БМП ( по
теореме о БМП)
)-
БМП ( по теореме о БМП)
 - БМП ( по теореме
о БМП). По теореме об общем виде сходящихся
послед. Поскольку
- БМП ( по теореме
о БМП). По теореме об общем виде сходящихся
послед. Поскольку
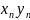 представили в виде суммы числа и БМП,
то она сходится, а это число является
ее пределом, т.е.
представили в виде суммы числа и БМП,
то она сходится, а это число является
ее пределом, т.е.

3)
если
 ,
то последов.
,
то последов.
 тоже содится и
тоже содится и

Доказательство:
пусть
 .
Докажем сначала что
.
Докажем сначала что
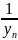 ограничена
ограничена
Рассмотрим
 тогда
тогда
 ;
;
 если
если
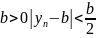 если
если
 если
если

В
случае
 – огр.
– огр.
Т.к.
 сходится то ее можно представить в виде
сходится то ее можно представить в виде

Анологично
 где
где

Осталось
доказать, что

Т.к.
 – БМП и
– БМП и
 - БМП, то и
- БМП, то и
 тоже БМП.
тоже БМП.
Ранее
дрказали. Что
ограничена, значит
 - БМП, как произведение бмп на огр.послед.
- БМП, как произведение бмп на огр.послед.
Итак
 где
где
 -
БМП, значит
-
БМП, значит
 сходится и
сходится и

8 Билет
Теорема о предельном переходе в неравенствах:
Если
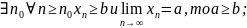 соотв.
соотв.

Доказательство(от
противного):пусть
 возьмем
возьмем
 – противоречия.
– противоречия.
Следствие1:
если

Следствие2:
если
 сходится, то
сходится, то

Доказательство:
расмотр.

 сходится как
разность сход.послед и
сходится как
разность сход.послед и

В
силу теор.о предельном переходе

Теорема о стабилизации знака в неравенстве:
Пусть

Доказательство:
расм.
Следствие:
если

Доказательство:
расм.
 .
Тогда в силу теор.о стабилизации знака
.
Тогда в силу теор.о стабилизации знака

9 Билет:
Теорема
о сжимающихся последовательностях или
о двух милиционерах:
пусть

Доказательство:
расм.

Т.к.

Возьмем

Итак
 .
Следовательно
.
Следовательно

10 Билет:
Опр1: послед. наз-ся:
Возраст. если
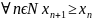
Убыв. Если

Монотонной, если послед. явл-ся возр. или убывающей
Строго возр.если

Строго убыв.если

Строго монотонной, если послед.явл-ся.строго возр.или строго убыв.
Опр2: послед.наз-ся:
Огр.сверху если

Огр.снизу если

Послед.наз-ся огран.если она ограничена и сверху и снизу
Опр3: число М наз-ся наименьшей верхней гранью или супремумом послед. Если М явл-ся н.в.гр. множества значений послед.
Число m наз-ся наиб.нижн.гр. или инфинимумом послед. если m явл-ся н.н.гр. множества значений пос-ти.
Критерий:

M=inf
Теорема о признаке сходимости монотонной послед-ти:
Возр.огран.сверху послед.сходится
Убывающая огр.снизу послед.сходится
Монотонная огр.послед.сход-ся
Доказательство: докажем что 1) и 2) док.одинаково, в 3) следует из 1 и2.
Т.к.
посед.огр.сверху, то она имеет конечный
sup .
.
a=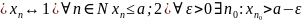 ;
расм.
.
В силу 1) и
2)
;
расм.
.
В силу 1) и
2)
 .
В силу монотонности
:
.
В силу монотонности
:
 .
Итак
.
Итак


