12 Билет:

Опр.: пусть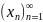 - последов.и пусть строго возрастающая послед.натур.чисел .выберем из послед. члены с номерами равными (k=1,2,3…) при этом получается новая последоват. Это последовательность последовательности.

Замечание: сама послед.явл-ся своей же послед. вообще говоря

Теорема: послед.сходится и только тогда когда сходится все ее посл-ти. При этом все подпослед-ти сходящейся посл-ти имеют один и тот же предел, равный пределу самой посл-ти.

Доказательство: пусть Пусть - произвольная подпослед-ть посл-ти . Докажем сто . . Расмотр. тогда если k , то . Следоа-но 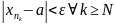. Итак

Пусть -послед-ть посл-ти и . Тогда и предел самой посл-ти тоже равен а, т.к. она явл-ся своей же посл-тью.

13 Билет:

Теорема Больльцано-Вейерштрасса:

Из огр.посл-ти можно выделить сходящуюся подпосл-ть.

Док-во: т.к. огр.то . Разобьем этот отрезок пополам и выберем в качестве отрезка [a1,b1] ту из его половин, которая содержит бесконечное число членов (если обе, то возьмем каждую из них)

Далее разобьем отрезок [a1,b1] пополам и возьмем в качестве [a2,b2] ту из его половин, которая в итоге получаем систему отрезков удовл.след.условиям:

1)

2)

По теореме о стяг.отрезках

Т.к. 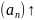и ;

Причем т.к. . Выберем [a1,b1] произвоьным образом. Далее выберем [a2,b2] так что n2>n1. Это можно сделать т.к. отрезок [a2,b2] содержит бесконечное число членов посл-ти значит и членов со сколь угодно большими номерами. Далее выберем [a3,b3] так что n3>n2 и т.д. на к-том шаге выберем

[aк,bк] так что и т.д. в итоге получаем посл-ть посл-ти так что . Мы знаем что , значит по теор.о сжимающ.посл.(о 2-х милиционерах)

14Билет:

Теорема критерий коши:

Послед-ть сходится тогда и только тогда, когда она фундаментальна.

Док-во: пусть посл-ть сходится, т.е.

Расмотр. n,m N |

Итак, | < фундоментальна.

Теперь, сначала докажем, что она огр.

| < в частности

Расм.множ-во {x1,x2….. это множ-во конечно значит

И M’=

Возьмем

Поскольку

Так как посл.огр. то по теор. Больцано-вейерштрасса - посл-ть так что

Докажем, что

Т.к.

Выберем номер N =

Тогда

Итак

16Билет:

Предел ф-ии в бесконечности:

Пусть ф-ия y=f(x) определена на неогранич.множ-ве

Опр1(по коши): число А наз-ся пределом ф-ии f(x) при x

Геометрически это означает что полосы огранич.гориз.прямыми y=A- при |x|>

Гр.ф-ии y=f(x) лежит внутри данной полосы.

Прямую y=A наз.гориз.асимптотой ф-ии если расст.от точек графика ф-ии до этой прямой стремится к 0 при и озночает что прямая y=A явл-ся гориз.асимптотой.

Опр2(по гейне): число А наз-ся пределом ф-ии y=f(x) при если

18 билет Теорема 1. (о предельном переходе в равенстве) Если две функции принимают одинаковые значения в окрестности некоторой точки, то их пределы в этой точке совпадают.

Þ .

Теорема 2. (о предельном переходе в неравенстве) Если значения функции f(x) в окрестности некоторой точки не превосходят соответствующих значений функции g(x) , то предел функции f(x) в этой точке не превосходит предела функции g(x).

Þ .

Теорема. Пусть две функции f и g, определённые на одном и том же невырожденном промежутке, содержащем число а, имеют в а пределы A,BeR: lim_af=A, limag = B. Если А < В, то существует окрестность точки а, в которой f(x) < g(x), за исключением, может быть, самой точки а. В частности, если f и g непрерывны в точке а и f(a) < g(a), то существует окрестность точки а, в которой f(x) < g(x). Доказательство. Поскольку точки А и В различны, у них существуют непересекающиеся окрестности. Например, если взять положительное число ε = (В — А)/2, ε-окрестность точки А расположена на числовой оси левее ε-окрестности точки В. По определению предела для этого ε найдутся положительные 6f и 6₆ такие, что при 0< |х - а| < 6f Α-ε<ί(χ)<Α + ε и (1) В - ε < g(x) < В + ε (2) при 0< |х - а| < 6_g. Тогда, взяв δ = min { δ>, 6_g } > О, при 0< |х - а| < δ получаем оба условия (1) и (2) одновременно. Значит, δ-окрестность точки а - искомая, т.к. f(x) < А + ε = (А + В)/2 = В - ε < g(x) при а-б<х<а + б, х*а. Если ещё f и g непрерывны в точке а, то f(x) < g(x) при всех хе(а-б, a+δ). ^ Следствие (о стабилизации знака). Допустим, сохраняя условие последней теоремы, что g(x)=0, т.е. lim_af < 0. Тогда f(x) < 0 в некоторой окрестности точки а, кроме, возможно, самой точки а. В частности, если f непрерывна в точке а и f(a) < 0, то f(x) < 0 в некоторой окрестности точки а. Аналогично, в случае lim_af > 0.

19 билет Непрерывность функции в точке

Определение 1. Функция у =f(х), определенная в некоторой окрестности точки а, называется непрерывной в точке а, если

Простейшими примерами непрерывных в любой точке а функций являются постоянная, функция у = с (поскольку ) и функция у = х (так как

Непрерывность в точке является локальным свойством функций

Использовав для предела функции определения «на языке бесконечно малых», «на языке окрестностей», получим соответствующие определения непрерывности функции, эквивалентные друг другу и определению 1. Наличие разных определений одного и того же понятия удобно тем, что в различных ситуациях полезным оказывается то или иное определение.

Чтобы сформулировать определение непрерывности «на языке бесконечно малых», введем понятие приращения функции: разность значений функции f(x) в точках х и а, т. е. f(х) — f(а) называют приращением функции и обозначают . Тогда получим следующее определение:

Определение 2. Функция у = f(х), определенная в некоторой окрестности точки а, называется непрерывной в точке а, если приращение функции бесконечно мало при .

Прежде чем сформулировать определения непрерывности «на языке - M» и на «языке окрестностей», заметим, что в случае непрерывности функции в точке а нельзя исключать из рассмотрения саму точку а. Поэтому соответствующие

определения примут следующий вид :

Определение 3. Функция y =f(x), определенная в некоторой окрестности точки а, называется непрерывной в точке а, если для любого >0, существует б>0 такое, что при всех х из неравенства |х — а| <б следует неравенство |f(x)-f(a)|< . Короче:

>0)( >0)( x: |x – a| <б)|f(x)-f(a)|<

Определение 4. Функция у =f(х), определенная в некоторой окрестности точки а, называется непрерывной в точке а, если для любого >0 можно указать такую б-окрестность точки а, в которой выполняется неравенство |f(x)-f(a)|< .

Используя свойства пределов, сформулируем соответствующие свойства непрерывных функций (их доказательства легко провести самостоятельно).

Теорема 1 (необходимое и достаточное условие непрерывности функции в точке).

Для того чтобы, функция у = f(х), определенная в некоторой окрестности точки а, была непрерывна в точке а, необходимо и достаточно, чтобы существовали односторонние пределы и равные друг другу и значению функции в точке а:

f(a-0)=f(a+0)=f(a).

Теорема 2 (о локальной ограниченности непрерывной функции).

Если функция непрерывна в точке, то она ограничена в некоторой окрестности этой точки.

Теорема 3 (о сохранении непрерывной функцией постоянного знака в окрестности точки).

Если функция у =f(х) непрерывна в точке а и f(a)>0 (f(а)<0), то в некоторой окрестности точки а выполняется неравенство f(x)>0 (f(x)<0).

Теорема 4 (об арифметических операциях над непрерывными функциями).

Если функции у =f(х} и у =g(х) непрерывны в точке а, то их сумма, произведение и частное (в случае g(а) 0) также

непрерывны, в точке а.

Используя последнюю теорему, нетрудно доказать такое утверждение.

Теорема 5. Всякая рациональная функция, т. е. функция вида, у = Р(х)/Q(х), где Р(х) и Q(х) — многочлены, непрерывна в любой точке а, в которой Q(a) 0.

Пример. Вычислить

Рассмотрим рациональную функцию f(x)= Ее знаменатель не обращается в нуль при х = — 1; значит, по теореме 5 функция непрерывна в точке х= —1. Тогда в силу определения 1 имеем . Таким образом находим

= =- .

ТОЧКИ РАЗРЫВА И ИХ КЛАССИФИКАЦИЯ

 Функция f(x) называется непрерывной в точке х0, если: 1 - Она определена в этой точке и её окрестности; 2 - Существуют односторонние пределы функции в этой точке; 3 - Односторонние пределы равны между собой; 4 - Значение функции в точке х0, равно пределу слева и равно пределу функции справо. Если в точке х0 нарушается хотя бы одно из условий (1 - 4), то точка х0 называется точкой разрыва функции.

Классификация:

1 - Если точка х0, является точкой разрыва функции, и при этом выполняется пункт №2, то х0 называется точкой разрыва 1-го рода. 2 - Если точкой х0 является точка разрыва, и при этом в ней нарушается пункт №2, то х0 - точка разрыва 2-го уровня 3 - Если х0 - точка разрыва функции, и при этом в ней выполнятеся пункты №2 ; №3 определения, то х0 - устранимая точка разрыва и относится к разрывам 1-го рода Точки разрыва следует искать среди точек, в которых функция неопределена и в точках смены видимости, если она не эллементарная. -Эллементарная : f(x) = ((x +2) * arctgx)/e^x -Не элементарная : f(x) = { 1-ая строчка х +2, х >= 2 ; 2-ая строчка e^x, x <2

20 билет Теорема. Если две функции и определены в одном и том же промежутке и обе непрерывны в точке то в той же точке будут непрерывны и функции

(последняя — при условии, что

Это непосредственно вытекает из теорем о пределе суммы, раз­ности, произведения и частного двух функций, имеющих порознь пре­делы

Остановимся для примера на частном двух функций. Предполо­жение о непрерывности функций и в точке равносильно наличию равенств.

Но отсюда, по теореме о пределе частного (так как предел знаме­нателя не нуль), имеем:

а это равенство и означает, что функция непрерывна в точке

Теорема. Функция непрерывна в точке  тогда и только тогда, когда бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции в точке, т. е. .

Докажем теорему. Пусть  непрерывна в точке .Тогда  по определению. Если обозначить , то  и тогда равенство, определяющее непрерывность, можно переписать так:  или  и тогда . Аналогично доказывается это утверждение в другую сторону: если , то .

Сформулируем основные теоремы о непрерывных функциях.

Теорема. Пусть заданные на одном и том же множестве Х функции и непрерывны в точке . Тогда функции , и (если ) непрерывны в точке .

Теорема (о непрерывности сложной функции). Пусть функция  непрерывна в точке , а функция  непрерывна в точке . Тогда сложная функция непрерывна в точке .

Всевозможные арифметические комбинации простейших элементарных функций, которые рассматривают в школьном курсе алгебры и начал анализа, мы будем называть элементарными функциями. Например, является элементарной.

Все элементарные функции непрерывны в области определения. Так что  всюду непрерывна, так как всюду определена, а функция  разрывна в точке .

Дадим теперь классификацию точек разрыва функции. Возможны следующие случаи.

1. Если  и существуют и конечны, но не равны друг другу, то точку называют точкой разрыва первого рода. При этом величину называют скачком функции в точке .