1 Билет:

Опр. Числовой последовательностью наз. любое отображение множества натуральных чисел в множество R

Способы задания ЧП:

1)Аналитический: если задается формула её n-ого члена:x_n=f(n);x_n=2n-1; 2)Описательный: объясняет из каких элементов строится последовательность;2,3,5-возр. последоват.;1,1,1-стац. последов. 3)Рекуррентный: указывает правило ,позволяющее вычислить n-й член последовательности если известны её предыдущие:x₁=1,x₂=1,x_n=x_n-2+x_n-1;

Арифмитические операции

Опр. Суммой последовательностей называется последовательность т.е.

Частным последоват. где называется послед. т.е.

Виды ЧП:

Опр1.Последовательность {x_n} называется ограниченной сверху(снизу),если существует число M(числоm) такое,что любой элемент x_n этой последовательности удовлетворяет неравенству x_n≤M(x_n≥m);

Опр2. Последовательность {x_n} называется ограниченной,если она ограничена и сверху и снизу,т.е. существуют числа mи Mтакие,что любой элемент x_nэтой последовательности удовлетворяет неравенству m≤ x_n ≤M;

Опр3.Последовательность {x_n} называется неограниченной ,если для любого положительного числаАсуществует элемент x_n этой последовательности, удовлетворяющей неравенству [x_n]>A(т.е. x_n>A или x_n<-A);

2 Билет:

Опр1. Число а называется пределом последовательности {x_n}, если для любого числа £ существует номер Nтакой,что при n>N выполняется неравенство [x_n-a]<£;

Опр2. Последовательность имеющая предел ,называется сходящейся. Если последовательность {x_n} сходится и имеет своим пределом число а,то символически это записывается так: =1;

Опр3.Последовательность,не являющая сходящейся,называется расходящейся.

Пример: Докажем что =1;

Возьмем любое £>0,т.к. [x_n-1]=[ ,то для нахождения значенияn,удовлетворяет неравенству[x_n-1]<£,достаточно решить неравенство откуда получаем n>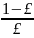 .Следовательно, в качестве N можно взять целую часть числа ,т.е. N=[ ].Тогда неравенство [x_n-1]<£ будет выполнятся при всех n>N.Этим и доказано,что =1.

Лемма1. Если все элементы бесконечно малой последовательности{a_n} равны одному и тому же числу с,тос=0;

Доказательство:Предположимобратное,т.е. что число с≠0.Предположим что £= . Тогда по определению БМП существует номер Nтакой,что при n>N выполняется неравенство [α_n]<£. Так как α_n=с, а £= ,то последнее неравенство можно переписать в виде [c]< , откуда 1< . Получили противоречие => с=0;

Теорема1. Сходящаяся последовательность имеет только один предел.

Доказательство:предположимобратное,т.е. что сходящая последовательность {x_n} имеет 2 предела а и в.Тогда по формуле x_n=a+α_n получаем x_n=a+α_nи x_n=в+β_n, где α_n и β_n –элементы БМП { α_n} и { β_n}. Приравниваем правые части этих соотношений ,найдем что α_n-β_n=в-а.Так как все элементы БМП {α_n-β_n} равны одному и тому же числу в-а,то по лемме1 в-а=0,т.е. в=а.

Теорема2.Сходящаяся последовательность ограничена.

Доказательство:Пусть {x_n} –сходящаяся последовательность и число а-её предел ,пусть £-произвольное положительное число и N-номер,начиная с которого выполняется неравенство [x_n-a]<£.Тогда [x_n]=[(x_n-a)+a]≤[x_n-a]+[a]<[a]+£, для любых n>N.Пусть А=max{[a]+£,[x₁],[x₂],…,[x_n]}.Очевидно ,[x_n]≤A для всех номеров n,что и означает ограниченность последовательности {x_n}.