Инварианты электромагнитного поля.

ИНВАРИАНТЫ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ - величины, характеризующие эл--магн. поле и не изменяющие своего значения (инвариантные) при переходе от одной инерциальной системы отсчёта к другой. И. э. п., как и само поле, являются ф-циями пространственных координат и времени. В вакууме существуют 2 независимых И. э. п.:

I₁=B²-E², I₂=(E.B).

Для эл--магн. поля в среде добавляются ещё 2 И. э. п.:

I₃=H²-D², I₄=(D.H).

Здесь Е и Н - векторы напряжённостей электрнч. и магн. полей соответственно, D и В - векторы индукции этих полей (в вакууме E=D и В=H, следовательно, I₁=I₃, I₂=I₄). Инвариант I₁ определяет ф-цию Лагранжа для эл--магн. поля в вакууме. Величины I₂ и I₄, строго говоря, являются псевдоинвариантами: они меняют знак при преобразованиях отражения и инвариантны относительно преобразований вращения (т. е. являются псевдоскалярами); истинными инвариантами являются I²₂ и I²₄. Инвариантность приведённых выражений следует из Лоренца преобразований для эл--магн. поля. И. э. п. являются инвариантными комбинациями компонентов тензоров электромагнитного поля F_mv и H_mv: 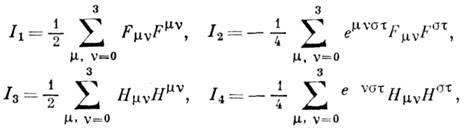   где e^mvst - Леви-Чивиты символ ,верх. и ниж. индексы относятся соответственно к контравариантным и ковариантиым компонентам тензора (см. Ковариантность и контравариантпостъ), связанным между собой при помощи метрич. тензора g_mv=g^mv:    Ковариантный тензор эл--магн. поля F_mv задаётся в 4-мерном пространстве (ct, x, у, z) (с - скорость света, t - время, х, у, z - пространственные координаты) следующим образом: 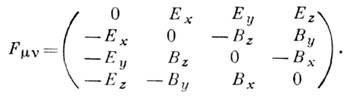   Тензор Н_mv получается из F_mv заменой    Вид тензоров эл--магн. поля и выражения для И. э. п. через их компоненты зависят от способа введения 4-мерного пространства: (ct, х, у, z) или (ict, х, у, z), в последнем случае нет необходимости различать ковариантные и контравариантные объекты. Инвариантность величин I_1,2,3,4 позволяет без непосредств. обращения к преобразованиям Лоренца сделать нек-рые выводы о связях между эл--магн. полями в разл. инерциальных системах отсчёта, напр.: переходом в др. систему отсчёта нельзя преобразовать чисто электрич. поле (Е№0, В=0)в чисто магн. (B№0, E=0) и наоборот; переходом в другую систему нельзя преобразовать острый (тупой) угол между векторами Е и В в тупой (острый); условия равенства полей Е=В или их ортогональности E^B (в этом случае I₁=0 или I₂=0) могут быть выполнены только одновременно во всех инерциальных системах отсчёта. В частности, для поля плоской эл--магн. волны в вакууме оба инварианта поля равны нулю.

Резонанс токов вцепи с индуктивностью и ёмкостью.

Рассмотрим электрическую цепь, состоящую из двух параллель­ных ветвей, одна из которых содержит активное сопротивление r₁ и индуктивное x₁, а другая — активное сопротивление r₂ и емкост­ное x₂ (рис. 161).

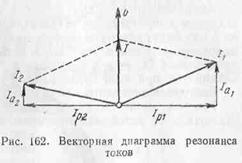
Если реактивные составляющие токов в ветвях с индуктивностью I₁ и емкостью I_С равны между собой (рис. 162), т. е. I_L = Iс, то ток  I на неразветвленном участке цепи совпадает по фазе с напряжением U, а угол j_общ== 0, соs j_общ = 1. Этот случай называется резонансом       токо

.

При резонансе токов реак­тивные токи — индуктив­ный и емкостный — взаим­но компенсируются, так что из сети поступает в цепь только   активный  ток I =I_a1+I_a2.

 

При надлежащем выбо­ре индуктивности L, емко­сти С или частоты f питаю­щей сети можно получить явление резонанса токов в разветвленной цепи. Ток I в общей неразветвленной части цепи при резонансе токов может быть значительно меньше, чем токи в ветвях с индуктивностью и емкостью. Явление резонанса токов используется в схемах радиотехники и в электротехнических установках.

Системы уравнений Максвелла

Дифференциальная форма

Уравнения Максвелла представляют собой в векторной записи систему из четырёх уравнений, сводящуюся в компонентном представлении к восьми (два векторных уравнения содержат по три компоненты каждое плюс два скалярных^[28]) линейных дифференциальных уравнений в частных производных первого порядка для 12 компонент четырёх векторных функций ( ):

Название	СГС	СИ	Примерное словесное выражение
Закон Гаусса			Электрический заряд является источником электрической индукции.
Закон Гаусса для магнитного поля			Не существует магнитных зарядов.[~ 1]
Закон индукции Фарадея			Изменение магнитной индукции порождает вихревое электрическое поле.[~ 1]
Теорема о циркуляции магнитного поля			Электрический ток и изменение электрической индукции порождают вихревое магнитное поле

Жирным шрифтом в дальнейшем обозначаются векторные величины, курсивом — скалярные.

Введённые обозначения:

•  — плотность стороннего электрического заряда (в единицах СИ — Кл/м³);

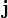•  — плотность электрического тока (плотность тока проводимости) (в единицах СИ — А/м²); в простейшем случае — случае тока, порождаемого одним типом носителей заряда, она выражается просто как  , где   — (средняя) скорость движения этих носителей в окрестности данной точки, 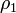  — плотность заряда этого типа носителей (она в общем случае не совпадает с  )^[29]; в общем случае это выражение надо усреднить по разным типам носителей;

•  — скорость света в вакууме (299 792 458 м/с);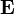

•  — напряжённость электрического поля (в единицах СИ — В/м);

•  — напряжённость магнитного поля (в единицах СИ — А/м);

•  — электрическая индукция (в единицах СИ — Кл/м²);

•  — магнитная индукция (в единицах СИ — Тл = Вб/м² = кг•с⁻²•А⁻¹);

•  — дифференциальный оператор набла, при этом:

 означает ротор вектора,

 означает дивергенцию вектора.

Приведённые выше уравнения Максвелла не составляют ещё полной системы уравнений электромагнитного поля, поскольку они не содержат свойств среды, в которой возбуждено электромагнитное поле. Соотношения, связывающие величины  ,  ,  ,   и   и учитывающие индивидуальные свойства среды, называютсяматериальными уравнениями.