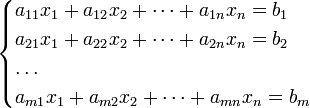Действия над матрицами.

1. Сложение матриц - поэлементная операция

2. Вычитание матриц - поэлементная операция

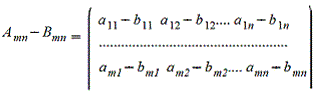
3. Произведение матрицы на число - поэлементная операция

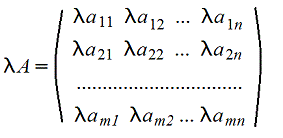
4. Умножение A*B матриц по правилу строка на столбец (число столбцов матрицы А должно быть равно числу строк матрицы B)

A_mk*B_kn=C_mn причем каждый элемент с_ij матрицы C_mn равен сумме произведений элементов i-ой строки матрицы А на соответствующие элемеенты j-го столбца матрицы B , т.е.

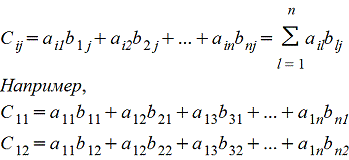
Покажем операцию умножения матриц на примере

5. Возведение в степень

m>1 целое положительное число. А - квадратная матрица (m=n) т.е. актуально только для квадратных матриц

6. Транспонирование матрицы А. Транспонированную матрицу обозначают A^T или A'

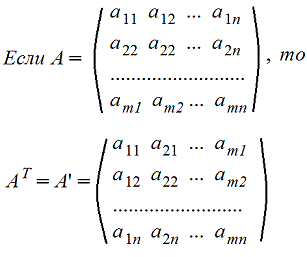
Строки и столбцы поменялись местами

3. Обра́тная ма́трица — такая матрица A⁻¹, при умножении на которую, исходная матрица A даёт в результате единичную матрицу E:

Если определитель матрицы равен нулю, то обратная к ней не существует.

Находим сначала детерминант матрицы А 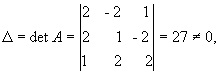     значит, обратная матрица существует и мы ее можем найти по формуле: 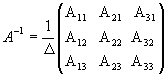  , где А_{i j} (i,j=1,2,3) - алгебраические дополнения элементов а_{i j} исходной матрицы.                    

                    

                   

                  

 откуда    .

4. Система m линейных алгебраических уравнений с n неизвестными (или, линейная система, также употребляется аббревиатура СЛА́У) в линейной алгебре — это система уравнений вида

(1)

Система линейных уравнений от трёх переменных определяет наборплоскостей. Точка пересечения является решением.

Здесь   — количество уравнений, а   — количество неизвестных. x₁, x₂, …, x_n — неизвестные, которые надо определить. a₁₁,a₁₂, …, a_mn — коэффициенты системы — и b₁, b₂, … b_m — свободные члены — предполагаются известными^[1]

Система линейных уравнений может быть представлена в матричной форме как:

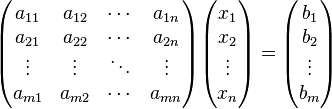
или:

.

Здесь   — это матрица системы,   — столбец неизвестных, а   — столбец свободных членов. Если к матрице   приписать справа столбец свободных членов, то получившаяся матрица называется расширенной.

Система линейных уравнений может:

1) Иметь единственное решение. 2) Иметь бесконечно много решений. 3) Не иметь решений (быть несовместной).

Метод Гаусса - метод последовательного исключения переменных. С помощью элементарных преобразований строк расширенной матрицы D системы матрицу A системы приводят к ступенчатому виду.

Решите систему уравнений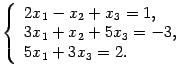 

Решение. Выписываем матрицу системы 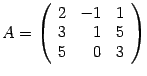  и столбец свободных членов   .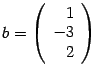

Находим определитель системы: 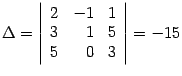  . Определитель отличен от нуля, следовательно, можно применить правило Крамера. Находим дополнительные определители:

Итак,