4. Дифференциальные уравнения первого порядка в симметричной форме.

Простейшие дифференциальные уравнения первого порядка — класс дифференциальных уравнений первого порядка, наиболее легко поддающихся решению и исследованию. К нему относятся уравнения в полных дифференциалах, уравнения с разделяющимися переменными, однородные уравнения первого порядка и линейные уравнения первого порядка. Все эти уравнения можно проинтегрировать в конечном виде.

Отправной точкой изложения будет служить дифференциальное уравнение первого порядка, записанное в т. н. симметричной форме:

где функции   и   определены и непрерывны в некоторой области  .

15( 3-II). Линейные однородные дифференциальные уравнения (определитель Вронского и условия линейной зависимости и независимости системы функций, структура общего решения, формула Лиувилля-Остроградского и ее практическое применение).

Определитель Вронского. Линейная зависимость и независимость системы функций.  Опр. 14.5.3.1. Система функций y₁(x), y₂(x), …, y_n(x) называется линейно зависимой на интервале (a, b), если существует набор постоянных коэффициентов  , не равных нулю одновременно, таких, что линейная комбинация этих функций тождественно равна нулю на (a, b):   для  .  Если равенство   для   возможно только при  , система функций y₁(x), y₂(x), …, y_n(x) называется линейно независимой на интервале (a, b).  Другими словами, функции y₁(x), y₂(x), …, y_n(x) линейно зависимы на интервале (a, b), если существует равная нулю на (a, b) их нетривиальная линейная комбинация. Функции y₁(x),y₂(x), …, y_n(x) линейно независимы на интервале (a, b), если только тривиальная их линейная комбинация тождественно равна нулю на (a, b).  Примеры: 1. Функции 1, x, x², x³ линейно независимы на любом интервале (a, b). Их линейная комбинация  - многочлен степени   - не может иметь на (a, b)больше трёх корней, поэтому равенство   = 0 для   возможно только при  .  Пример 1 легко обобщается на систему функций 1, x, x², x³ , …, xⁿ. Их линейная комбинация - многочлен степени   - не может иметь на (a, b) больше n корней.  3. Функции   линейно независимы на любом интервале (a, b), если  . Действительно, если, например,  , то равенство   имеет место в единственной точке  .  4. Система функций   также линейно независима, если числа k_i (i = 1, 2, …, n) попарно различны, однако прямое доказательство этого факта достаточно громоздко.  Как показывают приведённые примеры, в некоторых случаях линейная зависимость или независимость функций доказывается просто, в других случаях это доказательство сложнее. Поэтому необходим простой универсальный инструмент, дающий ответ на вопрос о линейной зависимости функций. Такой инструмент - определитель Вронского.

Опр. 14.5.3.2. Определителем Вронского (вронскианом) системы n - 1 раз дифференцируемых функций y₁(x), y₂(x), …, y_n(x) называется определитель

.

(26)

14.5.3.3.Теорема о вронскиане линейно зависимой системы функций. Если система функций y₁(x), y₂(x), …, y_n(x) линейно зависима на интервале (a, b), то вронскиан этой системы тождественно равен нулю на этом интервале.  Док-во. Если функции y₁(x), y₂(x), …, y_n(x) линейно зависимы на интервале (a, b), то найдутся числа  , из которых хотя бы одно отлично от нуля, такие что

для  .

(27)

Продифференцируем по x равенство (27) n - 1 раз и составим систему уравнений    Будем рассматривать эту систему как однородную линейную систему алгебраических уравнений относительно  . Определитель этой системы - определитель Вронского (26). При   эта система имеет нетривиальное решение  , следовательно, в каждой точке её определитель равен нулю. Итак, W(x) = 0 при  , т.е.   на (a, b).

Формула Лиуви́лля-Острогра́дского — формула, связывающая определитель Вронского (вронскиа́н) для решений дифференциального уравнения и коэффициенты в этом уравнении.

Пусть есть дифференциальное уравнение вида

тогда   где   — определитель Вронского

Для линейной однородной системы дифференциальных уравнений

 где   — непрерывная квадратная матрица порядка  , справедлива формула Лиувилля-Остроградского

 где   — след матрицы 

Правило дифференцирования определителя размерности 

Пусть 

Тогда для производной   верно

(в  -м слагаемом продифференцирована  -я строка)

Доказательство для линейного дифференциального уравнения произвольного порядка

Линейное дифференциальное уравнение  -го порядка

эквивалентно следующей системе

с матрицей   следующего вида

Вронскианы исходного уравнения и системы совпадают, а след матрицы   равен  . Подстановкой в формулу для системы получаем

Применение формулы Лиувилля-Остроградского

Пусть известно решение   линейного обыкновенного дифференциального уравнения второго порядка. Используя формулу Лиувилля-Остроградского возможно найти линейно независимое от него решение   той же системы.

Распишем вронскиан:

 поэтому

Так как для линейной независимости   и   достаточно  , приняв   получим 

Пример

Пусть в уравнении   известно частное решение  . Воспользовавшись формулой Лиувилля-Остроградского, получим

Тогда общее решение однородного уравнения
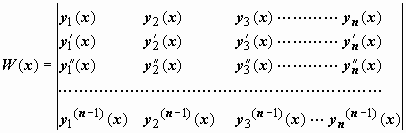