5 Билет

(классическое определение вероятности). Вероятностью события А называют отношение числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу.

Итак, вероятность события А определяется формулой:

 (1)

ЧАСТОТА появления случайного события - отношение m/n, числа m появлений этого события в данной последовательности испытаний к общему числу n испытаний.

Основные свойства вероятности. Пусть задано пространство элементарных событий  Е  , а вероятности  Р  определены на событиях из Е . Тогда:

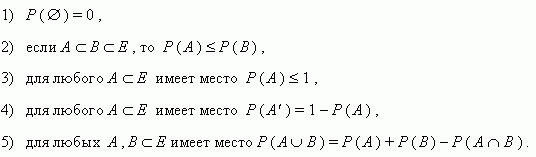
Геометрическая вероятность

Классическое определение вероятности связано с понятием элементарного события. Рассматривается некий набор Ω равновероятных событий A_i, которые в совокупности дают достоверное событие. И тогда все хорошо: всякое событие разбивается на элементарные, после чего считается его вероятность.

Однако, далеко не всегда исходный набор Ω (т.е. пространство всех элементарных событий) является конечным. Например, в качестве Ω можно взять ограниченное множество точек на плоскости или отрезок на прямой.

В качестве события A можно рассмотреть любую подобласть области Ω. Например, фигуру внутри исходной фигуры на плоскости или отрезок, лежащий внутри исходного отрезка на прямой.

Заметим, что элементарным событием на таком множестве может быть только точка. В самом деле, если множество содержит более одной точки, его можно разбить на два непустых подмножества. Следовательно, такое множество уже неэлементарно.

Теперь определим вероятность. Тут тоже все легко: вероятность «попадания» в каждую конкретную точку равна нулю. Иначе получим бесконечную сумму одинаковых положительных слагаемых (ведь элементарные события равновероятны), которые в сумме по-любому больше P(Ω) = 1.

Итак, элементарные события для бесконечных областей Ω — это отдельные точки, причем вероятность «попадания» в любую из них равна нулю. Но как искать вероятность неэлементарного события, которое, подобно Ω, содержит бесконечное множество точек? Вот мы и пришли к определению геометрической вероятности.

Определение

Геометрическая вероятность события A, являющегося подмножеством множества Ω точек на прямой или плоскости — это отношение площади фигуры A к площади всего множества Ω:

2) Для наглядности строят различные графики статистического распределения.

По данным дискретного вариационного ряда строят полигон частот или относительных частот.

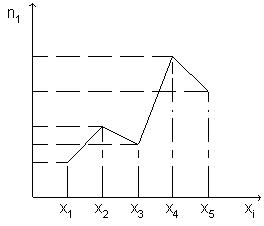
Полигоном частот называют ломанную, отрезки которой соединяют точки (x₁; n₁), (x₂; n₂), ..., (x_k; n_k). Для построения полигона частот на оси абсцисс откладывают варианты x_i, а на оси ординат - соответствующие им частоты n_i. Точки ( x_i; n_i) соединяют отрезками прямых и получают полигон частот (Рис. 1).

Полигоном относительных частот называют ломанную, отрезки которой соединяют точки (x₁; W₁), (x₂; W₂), ..., (x_k; W_k). Для построения полигона относительных частот на оси абсцисс откладывают варианты x_i, а на оси ординат - соответствующие им относительные частоты W_i. Точки ( x_i; W_i) соединяют отрезками прямых и получают полигон относительных частот.

В случае непрерывного признака целесообразно строить гистограмму.

Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиной h, а высоты равны отношению n_i / h (плотность частоты).

Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии n_i / h.

Площадь i - го частичного прямоугольника равна hn_i / h = n_i - сумме частот вариант i - го интервала; следовательно, площадь гистограммы частот равна сумме всех частот, т.е. объему выборки.

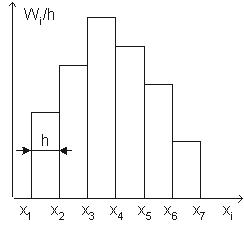
Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиной h, а высоты равны отношению W_i / h (плотность относительной частоты).

Для построения гистограммы относительных частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии W_i / h (Рис. 2).

Площадь i - го частичного прямоугольника равна hW_i / h = W_i - относительной частоте вариант попавших в i - й интервал. Следовательно, площадь гистограммы относительных частот равна сумме всех относительных частот, т.е. единице. 

Рис. 1. Полигон частот

Рис. 2. Гистограмма относительных частот