2 Билет

Формула бинома Ньютона

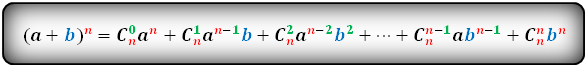
Треугольник Паскаля.

Число различных комбинаций элементов, составленных из различных групп, вида (а¹, а²,... , а^r), где а¹ - элемент l-й группы, содержащей n₁ элементов, равно n₁ ∙ n₂...∙ n_r.

3 Билет

Случа́йное собы́тие — подмножество множества исходов случайного эксперимента; при многократном повторении случайного эксперимента частота наступления события служит оценкой его вероятности.

Случайное событие, которое никогда не реализуется в результате случайного эксперимента, называется невозможным и обозначается символом  . Случайное событие, которое всегда реализуется в результате случайного эксперимента, называется достоверным и обозначается символом  .

Операции над событиями

1. Событие C называется суммой A+B, если оно состоит из всех элементарных событий, входящих как в A, так и в B. При этом если элементарное событие входит и в A, и в B, то в C оно входит один раз. В результате испытания событие C происходит тогда, когда произошло событие, которое входит или в A или в B. Сумма произвольного количества событий   состоит из всех элементарных событий, которые входят в одно из Ai, i=1, ..., m.

 

 2. Событие C произведением A и B, если оно состоит из всех элементарных событий, входящих и в A, и в B. Произведением произвольного числа событий   называется событие состоящее из элементарных событий, входящих во все Ai, i=1, ..., m.

 3. Разностью событий A-B называется событие C, состоящее из всех элементарных событий, входящих в A, но не входящих в B.

 

 4. Событие   называется противоположным событию A, если оно удовлетворяет двум свойствам.

Формулы де Моргана:     и  

 

5. События A и B называются несовместными, если они никогда не могут произойти в результате одного испытания.

События A и B называются несовместными, если они не имеют общих элементарных событий.

C=AxB=V

Тут V - пустое множество.

4 Билет

Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперед неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены.

Обозначать случайные величины прописными буквами X, Y, Z, а их возможные значения — соответствующими строчными буквами х, у, z..

Случайные величины подразделяться на дискретные(дсв) и непрерывные(нсв).

Дискретной  называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями. Число возможных значений дискретной случайной величины может быть конечным или бесконечным.

Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка. Очевидно, число возможных значений непрерывной случайной величины — бесконечно.

Законом распределения дискретной случайной величины называют соответствие между возможными значениями и их вероятностями; его можно задать таблично, аналитически (в виде формулы) и графически.

Биноминальным называют распределение вероятностей, определяемое формулой Бернулли.

Закон назван «биноминальным» потому, что правую часть равенства  можно рассматривать как общий член

разложения бинома Ньютона

Эта формула выражает закон распределения Пуассона вероятностей массовых (n велико) редких (p мало) событий.

Имеются специальные таблицы пользуясь которыми можно найти Рn(k) зная к и λ.

2) Выборка или выборочная совокупность — множество случаев (испытуемых, объектов, событий, образцов), с помощью определённой процедуры выбранных из генеральной совокупности для участия в исследовании.

Характеристики выборки:

• Качественная характеристика выборки – кого именно мы выбираем и какие способы построения выборки мы для этого используем.

• Количественная характеристика выборки – сколько случаев выбираем, другими словами объём выборки.

Статистические ряды распределения представляют собой упорядоченное распределение единиц совокупности  по группам и группировкам.  Ряды распределения изучают структуру совокупности, позволяют изучить ее однородность, размах и границы. Ряды распределения, образованные по качественным признакам, называютатрибутивными. При группировке по количественному признаку выделяются вариационные ряды. Вариационные ряды – ряды распределения единиц совокупности по признакам, имеющим количественное выражение, т. е. образованы численными значениями. 

Вариационные ряды по строению делятся на:

1. Дискретные (прерывные) – основаны на прерывных вариациях признака. Это такие ряды, где значения вариант имеют значения целых чисел (т. е. не могут принимать дробные значения). Дискретные признаки отличаются друг от друга на некоторую конкретную величину.

2. Интервальные (непрерывные) – имеют любые, в том числе и дробные количественные выражения и представлены в виде интервалов. Непрерывные признаки могут отличаться один от другого на сколь угодно малую величину.

Вариационные ряды имеют два элемента:

1. варианта (x)

2. частота (f)

Варианта – отдельное значение варьируемого признака, которое он принимает в ряду распределения.

Частота – численность отдельных вариант или каждой группы вариационного ряда. В некоторых случаях применяется частость. Частоты, выраженные в % или долях процента, называются частостями и рссчитываются как отношение локальной частоты варианты к сумме накопленных частот.

В свою очередь, частота бывает:

• локальной

• накопленной (кумулятивная – нарастающим итогом) 

Если вариационный ряд имеет неравные интервалы, то частоты в отдельных интервалах не сопоставимы, т. к. зависят от ширины интервала. В этих случаях рассчитывают плотность распределения, которая дает правильное представление о характере распределения вариант (единиц совокупности). Плотность распределения, в свою очередь, бывает:

• абсолютная плотность распределения – отношение частоты к величине (ширине) интервала

  

• относительная плотность распределения – отношение частости к ширине интервала

  

Интервалы	Локальная частота (f)	Накопленная частота (Σf)	Частость (ω)	Плотность распределения (φ)
20-30	3	3	0,3	0,03
30-40	5	8	0,5	0,05
40-50	1	9	0,1	0,01
50-60	1	10	0,1	0,01

Для характеристики рядов распределения применяются следующие показатели:

• средняя степенная

• мода

• медиана