Свойства
Операции ковариации и корреляции симметричны относительно своих аргументов;
Ковариация и корреляция между независимыми переменными равны 0;
;
;
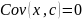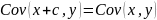Случайная переменная и закон её распределения. Закон распределения Фишера. Квантиль, f крит уровня и её расчёт в Excel.
Опр1. Случайной называют переменную которая в результате испытания примет одно и только одно возможное значение, наперед не известное и зависящее от случайных причин, которые невозможно заранее учесть.
Опр2. Переменная x с областью изменения X называется случайной, если свои возможные значения q из множества X переменная x принимает в результате некоторого опыта со случайными элементарными исходами вида .
Закон распределения – функция скалярного аргумента q, определенная на всей числовой прямой, характеризующую объективную возможность появления в опыте значений q случайной переменной x.
Полной характеристикой СП служит её дифференциальный закон распределения (ЗР). Так называется функция скалярного аргумента q, определённая на всей числовой прямой, характеризующая объективную возможность появления в опыте значений СП x. Если x – ДСП, то
Для дискретной величины
Случайная переменная (СП) x именуется дискретной (ДСП), если множество X состоит из конечного или счётного количества констант qi, то есть
X = {q1, q2, ..., qn }.
Для непрерывной величины
Если X есть некоторый интервал числовой прямой, конечный или бесконечный, то есть
X = (a, b), то СП x называется непрерывной (НСП).
Закон распределения Фишера
Пусть
-
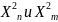две независимые случайные переменные,
имеющие
распределение
с числом степеней свободы n
и
m.
Случайная
переменная
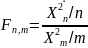называется дробью Фишера. Это позволяет
при любом альфа вычислить
,
удовлетворяющее уравнению
,
также называется
Fкрит
уровня
,это
(1-α)-квантиль
распределения Фишера с числом степеней
свободы n,m.
Эту
величины также можно вычислить в Excel,
используя функцию FРАСПОБР
по аргументам
.
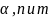Случайный вектор и его основные количественные характеристики (на примере вектора левых частей схемы Гаусса – Маркова при гомоскедастичном неавтокоррелированном остатке).
Рассмотрим
набор случайных переменных
.
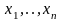Этот упорядоченный набор называется
случайным вектором и обозначается
:
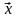(1)
Его основными характеристиками служат:
Вектор ожидаемых значений компонент:
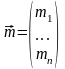
так
называют вектор констант, компоненты
которого – мат. ожидания компонент
вектора
.
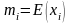Ковариационная матрица:
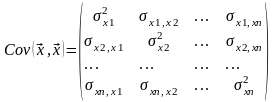(2)
По
главной диагонали располагаются
дисперсии компонент случайного вектора.
Недиагональные элементы это ковариации
компонентов. Например,
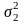- это дисперсия компоненты
вектора (1). Элемент
- это ковариация компонент
и
вектора (1) Матрица является симметричной.
Количественные характеристики
Свойство операции вычисления ожидаемого значения вектора.
Если
обобщить свойство
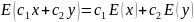на аффинное преобразование случайного
вектора
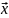в случайный вектор
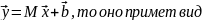
Свойство операции вычисления ковариационной матрицы случайного вектора.
Если
же обобщить свойство
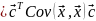на
аффинное преобразование случайного
вектора
в случайный вектор
.
13.Основные
количественные характеристики выхода
аффинного преобразования случайного
вектора (на примере вектора
мнк – оценок коэффициентов линейной
модели при гомоскедастичном
неавтокоррелированном остатке).
Рассмотрим набор
случайных переменных
.
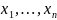Этот упорядоченный набор называется
случайным вектором и обозначается
:
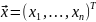(1)
Его основными характеристиками служат:
Вектор ожидаемых значений компонент:
так называют вектор
констант, компоненты которого – мат.
ожидания компонент вектора
.
Ковариационная матрица:
(2)
По главной диагонали
располагаются дисперсии компонент
случайного вектора. Недиагональные
элементы это ковариации компонентов.
Например,
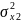- это дисперсия компоненты
вектора (1). Элемент
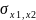- это ковариация компонент
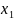и
вектора (1) Матрица является симметричной.
Количественные характеристики
Свойство операции вычисления ожидаемого значения вектора.
Если обобщить свойство на аффинное преобразование случайного вектора в случайный вектор
Свойство операции вычисления ковариационной матрицы случайного вектора.
Если же обобщить свойство
на аффинное преобразование случайного вектора в случайный вектор .