53. Модели нестационарных временных рядов. Идентификация модели тренда.

1. Аддитивная модель временного ряда имеет следующую спецификацию

(1)

Алгоритм выбора тренда T(t) в модели (1):

1. Наблюдаем уровни ряда y_t, для которого создаем модель (1)

2. Из наблюдаемых уровней отбираем уровни базовых периодов. Пусть отобрано m уровней базовых периодов: y₁, y₂,…,y_m. (2)

3. Вычисляем по уровням (2) при τ=1,2,…,m-1 разности Δy_τ=y_τ+1-y_τ

4. Задаваясь значениями τ=1,2,… и Δτ=1, вычисляем значения индикаторов функции тренда:

I₁(τ)=Δ⁽²⁾y_τ=Δy_τ+1-Δy_τ

I₂(τ)= Δ⁽³⁾y_τ=ΔI₁(τ)=I₁(τ+1)-I₁(τ)

I₃(τ)=Δ( )=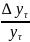

I₄(τ)=Δ(

I₅(τ)=Δ(τΔy_τ)=(τ+1)Δy_τ+1-τΔy_τ

I₆(τ)=Δ⁽²⁾(

5. Отмечаем те индикаторы, значения которых в ответ на изменение переменной τ, колеблются вокруг нуля. По данному индикатору выбираем соответствующую функцию тренда T(t) (наиболее простую):

- для I₁- линейная

-для I₂-парабола второго порядка

- для I₃-показательная

- для I_4-степенная

- для I₅-логарифмическая

- для I₆- логистическая

2. Модель броуновского движения

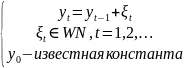
Временной ряд yt обладает следующими характеристиками

m_y(t)=y₀, σ_y²=σ_ξ²t, σ_yy(I,j)= σ_ξ²min(I,j)

53. Оценивание линейной модели с автокоррелированным остатком ar(1) алгоритмом Хильдретта – Лу.

М одель AR(1) имеет следующую спецификацию:

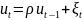
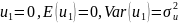
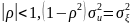
t, t-1

уравнение модели запишем в идее:

1. Задаемся на промежутке [0,1) набором пробных значений по правилу

(1)

где N-некоторое натуральное число

2. При каждом значении (1) составляем систему уравнений наблюдений

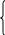
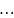
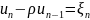
И вычислим на основании этой системы МНК-оценки ,

3. Выбираем из множества пробных значений (1) такую величину , при которой имеет место экстремум .

Выбранные величины и будут искомыми оценками параметров модели AR(1)

56. Проблема мультиколлинеарности, типы и симптомы мультиколлинеарности. Методика отбора регрессоров в линейной модели в ситуации мультиколлинеарности.

Мультиколлинеарность- ситуация, в которой в уравнениях наблюдений столбцы матрицы X становятся практически линейно зависимыми, что входит в противоречии с исходной предпосылкой теоремы Гаусса-Маркова. В ситуации мультиколлинеарности оценки параметров линейной регрессионной модели становятся ненадежными.

В условиях мультиколлинеарности текущий уровень ряда, как правило, может быть во многом объяснен предыдущими значениями

x_t≈c₀+c₁x_t-1+c₂x_t-2 (1)

Если (1) превращается в точное равенство, возникает ситуация совершенной мультиколлинеарности.

Симптомы:

1. резкое изменение значений оценок модели при незначительной вариации состава обучающей выборки;

2. наличие в оцененной модели небольших по модулю значений 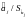при достаточно высоком значении коэф-та детерминации;

3. большое значение коэф-та детерминации между каждой объясняющей пер-ой линейной модели и ее остальными объясняющими пер-ми.

Отбор объясняющих переменных методом дополнительной регрессии

2 принципа такого отбора:

- в модели следует оставлять только значащие факторы, используя при определении значащих факторов T-тест

- при отборе фактора х_j в модель строится для этого фактора дополнительная регрессия

x_jt=b₀+b₁x_1,t+…+b_j-1x_j-1,t+b_j+1x_j+1,t+…+v_j,t и вычисляется R_j²

в модели сохраняются те факторы, у которых коэффициенты детерминации в дополнительной регрессии наименьшие, а коэффициента корреляции стремятся к максимуму