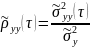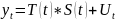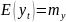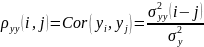- •1. Назначение экономико-математических моделей (эмм). Два принципа их спецификации. Типы уравнений в эмм: поведенческие уравнения и тождества (на примере макромодели).
- •2. Типы переменных в экономических моделях. Структурная и приведённая форма модели (на примере макромодели). Компактная запись.
- •4. Спецификация и преобразование к приведённой форме эконометрических моделей. Эконометрическая модель Самуэльсона–Хикса делового цикла экономики. Компактная запись.
- •Порядок оценивания линейной эконометрической модели из изолированного уравнения в Excel. Смысл выходной статистической информации функции линейн.
- •Случайная переменная и закон её распределения. Нормальный закон распределения и его параметры.
- •Случайная переменная и закон её распределения. Распределение хи-квадрат.
- •Случайная переменная и закон её распределения. Распределение Стьюдента, Квантиль, t крит уровня и её расчёт в Excel.
- •Ковариация Cov(X, y), и коэффициент корреляции, Cor(X, y) пары случайных переменных (X, y). Частная ковариация и частный коэффициент корреляции.
- •Свойства
- •Случайная переменная и закон её распределения. Закон распределения Фишера. Квантиль, f крит уровня и её расчёт в Excel.
- •Случайный вектор и его основные количественные характеристики (на примере вектора левых частей схемы Гаусса – Маркова при гомоскедастичном неавтокоррелированном остатке).
- •Случайный вектор и факторизация его ковариационной матрицы. Случайный вектор случайных остатков в схеме Гаусса – Маркова при гетероскедастичном неавтокоррелированном остатке.
- •Временной ряд и его структура (На примере ввп России).
- •Модели тренда временного ряда.
- •17. Моделирование сезонной составляющей при помощи фиктивных переменных.
- •18. Регрессионная зависимость случайных переменных. Функция регрессии, стандартные модели функции регрессии.
- •19.Схема Гаусса–Маркова (на примере модели Оукена).
- •20.Понятие статистической процедуры оценивания параметров эконометрической модели. Линейные статистические процедуры. Требования к наилучшей статистической процедуре.
- •21. Теорема Гаусса-Маркова: выражение вектора оценок коэффициентов и доказательство их несмещённости.
- •22. Теорема Гаусса-Маркова: выражение Cov( , ) и его обоснование.
- •24. Теорема Гаусса-Маркова: выражение .
- •25. Взвешенный метод наименьших квадратов (вмнк). Простейшая модель гетероскедастичности случайного остатка. Практическая реализация вмнк.
- •27. Система нормальных уравнений и явный вид её решения при оценивании методом наименьших квадратов (мнк) линейной модели парной регрессии (на примере модели Оукена).
- •28. Ковариационная матрица оценок коэффициентов линейной модели парной регрессии: явные выражения .
- •29.Свойства мнк-оценок параметров линейной модели множественной регрессии (лммр) при нормальном векторе случайных остатков: независимость случайных векторов
- •30.Свойства мнк-оценок параметров линейной модели множественной регрессии (лммр) при нормальном векторе случайных остатков: закон распределение оценки .
- •31. Свойства мнк-оценок параметров линейной модели множественной регрессии (лммр) при нормальном векторе случайных остатков: закон распределения дроби .
- •32. Оценивание параметров линейной модели множественной регрессии (лммр) при нормальном векторе случайных остатков методом максимального правдоподобия (ммп).
- •34. Спецификация и оценивание нелинейных по коэффициентам моделей множественной регрессии со специальными функциями регрессии (на примере производственной модели с функцией Кобба-Дугласа).
- •35. Оптимальное точечное прогнозирование значений эндогенной переменной по линейной модели (случай гомоскедастичного и неавтокоррелированного случайного остатка) на примере модели Оукена.
- •Тест Голдфелда-Квандта гомоскедастичности случайного остатка в лммр
- •37.Тест Дарбина–Уотсона отсутствия автокорреляции случайного остатка в лммр.
- •38.Коэффициент детерминации как мерило качества спецификации эконометрической модели (на примере модели Оукена). Скорректированный коэффициент детерминации.
- •39. Связь коэффициента детерминации с коэффициентом корреляции эндогенной переменной и её оценки (на примере модели Оукена).
- •41. Процедура интервального прогнозирования по оценённой линейной эконометрической модели значений эндогенной переменной (на примере модели Оукена).
- •42.Процедура проверки адекватности оценённой линейной эконометрической модели (на примере модели Оукена).
- •43.Последствия, симптомы и методика устранения ошибки спецификации эконометрической модели, состоящей в неверном выборе функции регрессии.
- •44.Последствия и симптомы ошибки спецификации линейной эконометрической модели, состоящей во включении незначимой объясняющей переменной.
- •45. Последствия и симптомы ошибки спецификации линейной эконометрической модели, состоящей в пропуске значимой объясняющей переменной.
- •46. Последствия и симптомы ошибки спецификации линейной эконометрической модели, состоящей в непостоянстве значений её параметров в области изменения объясняющих переменных; тест Чоу.
- •47. Основные характеристики временного ряда.
- •48. Стационарный временной ряд. Белый шум.
- •49.Оценка характеристик стационарного временного ряда.
- •Частная автокорреляционная функция стационарного временного ряда и алгоритм её оценивания.
- •Модель ar(p) и её идентификация.
- •Модель ma(q) и её идентификация.
- •Оптимальный линейный алгоритм прогнозирования уровней стационарного временного ряда.
- •Модели нестационарных временных рядов. Идентификация модели тренда.
- •Оценивание линейной модели с автокоррелированным остатком ar(1) алгоритмом Хильдретта – Лу.
- •Проблема мультиколлинеарности, типы и симптомы мультиколлинеарности. Методика отбора регрессоров в линейной модели в ситуации мультиколлинеарности.
- •Модели с лаговыми переменными: авторегрессионная модель и модель распределённых лагов; проблемы оценивания этих моделей.
- •Эконометрические модели в виде систем линейных одновременных уравнений (слоу): примеры и проблема идентификации (на примере модели спроса-предложения блага).
- •Эконометрические модели в виде систем линейных одновременных уравнений (слоу): примеры и проблема оценивания параметров структурной формы (на примере макромодели Кейнса).
- •60. Необходимое условие идентифицируемости поведенческого уравнения модели слоу (правило порядка)
- •61. Критерий идентифицируемости поведенческого уравнения модели слоу (правило ранга)
- •62. Понятие инструментальных переменных. Оценивание параметров структурной формы двухшаговым м-ом наименьших квадратов на примере простейшей макромодели Кейнса
- •63. Теорема Слуцкого и оценивание параметров структурной формы косвенным методом наименьших квадратов (кмнк) – на примере простейшей макромодели Кейнса.
47. Основные характеристики временного ряда.
Временным рядом
(динамическим рядом) называют экономическую
переменную
,
датированную
дискретным моментом времени,

(Альтернативное
определение) Временной ряд - упорядоченные
во времени значения некоторого
количественного показателя экономического
объекта (например, ВВП):

Основные модели временного ряда:
1 - аддитивная модель временного ряда, 2 - мультипликативная модель.
 тренд,
тренд,
 сезонная составляющая.
сезонная составляющая.
Сечения
(уровни) ряда как случайные переменные
- это значения, датированной переменной
в фиксированные моменты времени
(Например, при
 значения
значения
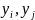 называются сечениями временного ряда
.
Расстояния во времени между сечениями
ряда
- это модуль разности временных моментов
этих сечений
называются сечениями временного ряда
.
Расстояния во времени между сечениями
ряда
- это модуль разности временных моментов
этих сечений
 .
Наличие случайного остатка означает,
что сечения (уровни) ряда
являются случайными переменными
.
Наличие случайного остатка означает,
что сечения (уровни) ряда
являются случайными переменными
Математические характеристики.
Математическое
ожидание
ряда
 - детерминированная функция времени,
вокруг графика которой "вьются"
графики реализаций временного ряда.
- детерминированная функция времени,
вокруг графика которой "вьются"
графики реализаций временного ряда.
Замечание:
значения
при каждом фиксированном
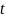 являются случайной переменной. Это
обстоятельство отметим
являются случайной переменной. Это
обстоятельство отметим
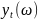 ,
где
,
где
 - символ элементарного исхода. На практике
экономисту доступна обычно только
некоторая реализация временного ряда
- символ элементарного исхода. На практике
экономисту доступна обычно только
некоторая реализация временного ряда
 .
.
Дисперсия
временного ряда

Автоковариационная
функция
ряда
 - функция двух аргументов
- функция двух аргументов
 ,
значения которой имеют смысл ковариаций
уровня ряда.
,
значения которой имеют смысл ковариаций
уровня ряда.
Автокорреляционная
функция ряда

48. Стационарный временной ряд. Белый шум.
Исходный временной ряд называется стационарным, если его основные характеристики удовлетворяют 3 требованиям:
математическое ожидание ряда является постоянным, т.е. не зависит от времени

Дисперсия ряда - некоторая константа
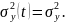
Автоковариационная функция зависит не от двух аргументов , а от одного аргумента
 - расстояние между сечениями.
- расстояние между сечениями.
 .
Автоковариационная функция стационарного
ряда - четная функция аргумента
.
.
Автоковариационная функция стационарного
ряда - четная функция аргумента
.

Белый шум. Стационарный ряд называется белым шумом, если его математическое ожидание равно 0, а сечения не коррелированы.

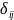 -
символ Кронекера,
-
символ Кронекера,
49.Оценка характеристик стационарного временного ряда.
Ряд
именуется стационарным, если его
ожидаемое значение и дисперсия постоянны
(не зависят от переменной времени t),
а автоковариационная и автокорреляционная
функции являются четными функциями
одного аргумента
 :
:
Ряд именуется нестационарным, если хотя бы одно условие 1-4 не выполняется.
основные характеристики временного ряда:
Математической ожидание ряда
Дисперсия временного ряда

Автоковариационная функция ряда
 – функция двух
аргументов
– функция двух
аргументов
 при перестановке которых значения
функций не меняются.
при перестановке которых значения
функций не меняются.
Автокорреляционная функция ряда

Оценки этих характеристик могут быть найдены по одной реализации этого ряда
Оценка математического ожидания:
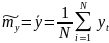
Оценка дисперсии:

Оценка автоковариационной функции:

Оценка автокорреляционной функции: