42.Процедура проверки адекватности оценённой линейной эконометрической модели (на примере модели Оукена).

1. Результаты наблюдений объекта сле­дует разделить на два класса. В первый класс (обучающую выборку) включить основ­ной объем результатов наблюдений 95% выборки. Оставшиеся результаты наблюдений (например, пара ( 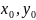)) составят контролирующую выборку.

2. По обучающей выборке оценить модель.

3. Задаться доверительной вероятностью и по значени­ям регрессоров, входящих в контролирующую выборку, построить доверительные интервалы для соот­ветствующих этим регрессорам значений эндогенной переменной модели ( ).

4. Проверить, попадают ли значения эндогенной переменной из контролирующей выборки в соответству­ющие доверительные интервалы (в интервал ). Если да, то признать оцененную модель адекватной; если нет, то оцененная модель не может быть признана адекватной и подлежит доработке.

Модель Оукена:

(1)

4. В обучающую выборку включим наблюдения за 2001 -2009 года; в контролирующую – наблюдения 2010 года.

5. Оцененная модель:

(2)

Оценки модели вычисляются с помощью функции ЛИНЕЙН для обучающей выборки ( ; ;1;1).

;

6. Вычислим при помощи оцененной модели (2) по значению прогноз величины : .

Далее определим стандартную ошибку прогноза:

, где . Так как модель Оукена – это модель парной регрессии, тo можно вычислить по формуле:

=0,19;

При доверительной вероятности и числе степеней свободы при помощи функции СТЬЮДРАСПОБР находим =2,37 и вычисляем границы доверительного интервала:

значение попадает в доверительный интервал , делаем вывод, что оцененная модель (2) адекватна и может быть использована для изучения объекта: прогноза темпа прироста реального ВВП по величине изменения уровня безработицы.

43.Последствия, симптомы и методика устранения ошибки спецификации эконометрической модели, состоящей в неверном выборе функции регрессии.

Пусть экономист составил спецификацию регрессионной модели (например, модель парной регрессии)

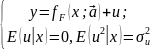(1)

с ошибочно функцией регрессии (2)

Для определенности будем полагать, что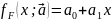 (3)

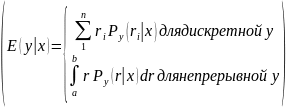(4)

Пусть истинная: функция регрессииу на x(4)имеет уравнение такое, что при любом векторе коэффициентов функции (3) и, по крайней мере, некотором значении х имеет место неравенство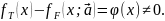 (6)

Данное неравенство означает; что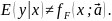 (7)

Из неравенства (7) следует, что заявленная в спецификации (1) предпосылка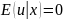 (8)является ложной, поскольку справедливо иное соотношение:

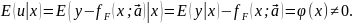(9)

Значит, последствием ошибочного выбора типа функции в урав­нении регрессии являетсянарушение предпосылки(8) о нулевомматематическом ожидании случайного остатка. Исходя из соотношения (9) при оценивании модели (1) с линейной функцией регрессии по обучающей выборке оказывается нарушенной предпосылка теоремы Гаусса-Маркова(о том, что 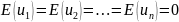). В итоге оценки коэффициентов модели (1): 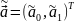(10) оказываются смешенными, а их характеристики точности утрачивают объективность. В конечном счете прогноз (точечный и интервальный) значения экзогенной переменной у, вычисленный при 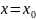по оцененной модели с ошибочной функцией регрессии

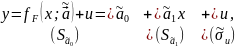(11)

оказывается неадекватным в силу того, что в основе прогноза прежде всего лежит (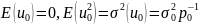 ) именно предпосылка (8):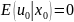

Главное последствие неверно выбранного типа функции регрессии — неадекватные прогнозы.

Симптомы:

1) несоответствие диаграммы рас­сеяния, построенной по выборке , графику функции (2)

2)длительное постоянство знака оценок случайных остатков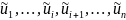 в упорядоченных уравнениях наблюдений(по возрастанию значений объясняющей перемен­ной). Этот симптом, называемый ложной корреляцией, можно выявить статистикой DWДарбина — Уотсона в динамических моделях с автокоррелированным остатком.

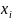3)Чтобы выявить третий симптом, следует разделить обучающую выборку на две примерно равные по количеству наблюдений части и (12) так, чтобы различие в элементах ,матрицX₁иX₂ - было по воз­можности существенным. Затем по каждой из выборок (12) оценить модель (1).Сильное отличие одноимен­ных коэффициентов в двух оцененных вариантах модели — третий симптом неверного выбора функции регрессии.

Методика устранения ошибки:Если наличие данной ошибки подтвердилось, следует, используя диаграмму рассеивания, выбрать более подходящую функцию регрессии и повторить процедуру построения регрессионной модели.