37.Тест Дарбина–Уотсона отсутствия автокорреляции случайного остатка в лммр.

Рассмотрим предпосылку №3 Теоремы Гауса-Маркова.Если эта предпосылка справедлива, то так же будет справедлива следующая гипотеза . Именно она проверяется тестом Дарбина-Уотсона.

Альтернативой гипотезы H₀ служит гипотеза H₁ о наличии положительной корелляции случайных остатков в соседних уравнениях наблюдений:

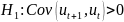
Замечание ; не редко, гипотеза H₁ справедлива в той ситуации, когда ошибочно выбрана модель функции регрессии(например, ошибочно выбрано, линейное уравнение этой функции или в линейной функции пропущены значащие объясняющие переменные)

Статистика критерия гипотезы H₀ вычисляется по следующему правилу: , где - оценка случайного остатка уравнений наблюдений t.

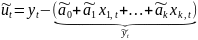, t=1,2,3,…n ;

Область изменения случайной переменной DW это интервал числовой прямой от 0 до 4. Можно проверить, что при справедливой гипотезе H₀ значение статистики DW концентрируется в окрестности константы =2.

Критерием гипотезы H₀ служит интервал числовой прямой I₁ – левой границей является число 0, а правой границей величина 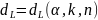, которая является функцией уровня знач. 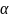, количество объясняющих переменных – k, n- число уравнений наблюдений.

Значение 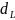выбирается из таблиц, рассчитанных автором теста Дарбина и Уотсоном. Областью применения гипотезы H₀ служит интервал I₃, левая граница которого 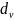так же выбирается из таблиц

Наконец, если статистика DW попадает в интервал I₂, то гипотезу H₀ нельзя не принять. Следует, для достижения определенности, количество уравнений наблюдений.

38.Коэффициент детерминации как мерило качества спецификации эконометрической модели (на примере модели Оукена). Скорректированный коэффициент детерминации.

Обратимся к выражению и перепишем его в след.виде : (*)

Первые слагаемые в правых частях уравнения объясняются предопределенными переменными модели; вторые слагаемые, напротив, предопределенными переменными не объясняются, т.к. порождены неучтенными в модели факторами.

Можно убедиться, что из уравнений (*) следует равенство

(**)

В левой части этого равенства расположена вариация эндогенной переменной модели – TSS; первое слагаемое в правой части – это та часть вариации эндогенной переменной, которая объясняется предопределенными переменными модели – RSS; второе слагаемое эта та часть вариации эндогенных переменных, которая порождена неучтенными факторами –ESS.

Разделим обе части уравнения (**) на величину TSS и перепишем его в следующем виде: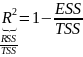

Величина носит название коэффициента детерминации модели, является случайной переменной и имеет смысл доли вариации эндогенной переменной, которая объясняется предопределенными переменными модели ( в рамках обучающей выборки), т.к. это доля, то 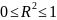и чем ближе тем удачнее выбрал экономист объясняющие переменные. Экономисты всегда размещают величину в записи оцененной модели. Если близко к 0, то те переменные плохо объясняют модель.

Замечание : при добавлении объясняющих переменных в модель, последнее(2-е) слагаемое в правой части (**), как правило уменьшается. След-но, возрастает, даже в той ситуации, когда доп.объясняющие переменные экономически не обоснованы.

В эконометрике помимо величины скорректированный коэффициент детерминации, который вычисляется по правилу:

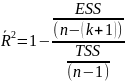
С добавлением объясняющих переменных в модель, этот коэффициент не обязательно увеличивается. Если при добавлении объясняющей переменной скорректированный коэффициент возрастает, то это служит сигналом целесообразности включения в модель соответствующей объясняющей переменной.