Моделирование экономических процессов в виде смо с однородными заявками
Пример СМО с однородными заявками – модель бензоколонки. Предприниматель собирается вложить деньги в строительство новой бензоколонки и хотел бы ориентировочно знать, какова должна быть оптимальная структура бензоколонки и на получение какой прибыли он может рассчитывать.
Представление модели бензоколонки как СМО.
Имеется поток клиентов, желающих быть обслуженными (в данном случае это поток автомашин, желающих заправиться бензином).
Имеются устройства или агрегаты, которые обеспечивают удовлетворение заявок клиентов (в данном случае одна или несколько раздаточных колонок).
Имеется определенный набор правил обслуживания клиентов (в данном случае можно, например, считать, что все клиенты равноправны, т.е. никто не имеет права на заправку вне очереди).
Концептуальная модель.
Пусть имеется СМО с переменным числом
каналов
,
которое может принимать любое значение
в диапазоне от одного до
.
Входной поток заявок – простейший,
следовательно, время между соседними
заявками имеет показательное распределение
с известным математическим ожиданием
(средним значением)
.
Время обслуживания заявки в любом канале
– величина случайная, имеющая показательное
распределение с известным средним
временем обслуживания
.
Все заявки однородны и независимы.
Правило (дисциплина) обслуживания
состоит в том, что очередная заявка
поступает в тот канал, который раньше
других освободился. Если время ожидания
начала обслуживания превышает заданную
величину
,
то заявка покидает СМО необслуженной.
Период функционирования СМО характеризуется
величиной
.
Входные характеристики модели.
Число каналов (1, …, ).
Среднее время между соседними заявками .
Среднее время обслуживания заявки .
Максимально допустимое время ожидания .
Период работы СМО .
Число случайных реализаций моделируемого процесса
.
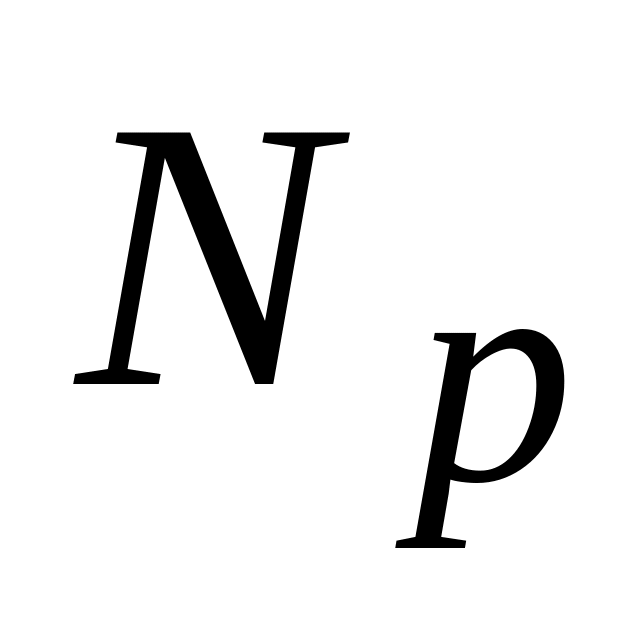Выходная характеристика модели:
среднее число обслуженных заявок
.
Выбор показателя и критерия эффективности.
В качестве основы для формирования показателя эффективности работы СМО будем рассматривать среднюю прибыль, определяемую по формуле:
,
где
– чистая прибыль, полученная в результате
обслуживания одной заявки;
– издержки обслуживания всех заявок,
зависящие от числа каналов.
Разделив обе части равенства на величину , получим следующее выражение для расчета показателя эффективности:
,
где
– средняя относительная прибыль.
Величину
(отношение издержек обслуживания к
чистой прибыли, полученной в результате
обслуживания одной заявки) будем
рассматривать как функцию числа каналов,
для которой необходимо подобрать
подходящую аппроксимацию. Примем
следующую аппроксимацию:
.
Окончательно имеем следующее выражение для показателя эффективности:
.
В качестве критерия выбора наивыгоднейшей структуры СМО примем оптимальное число каналов, обеспечивающее максимум средней относительной прибыли:
,
где
– оптимальное число каналов.