Имитационное моделирование случайных величин с произвольным распределением

Задача. Требуется смоделировать случайную величину Y, имеющую заданную плотность распределения f(x) с помощью случайной величины  с равномерным распределением на отрезке [0,1].

Принцип моделирования. Плотность распределения f(x) аппроксимируется кусочно-постоянной функцией, определенной на интервале . Это значит, что данный интервал разбит на n частичных интервалов , , плотность распределения на каждом из которых принимается постоянной. Величины , , выбираются так, чтобы вероятности попадания в любой частичный интервал были одинаковы, т.е.

, .

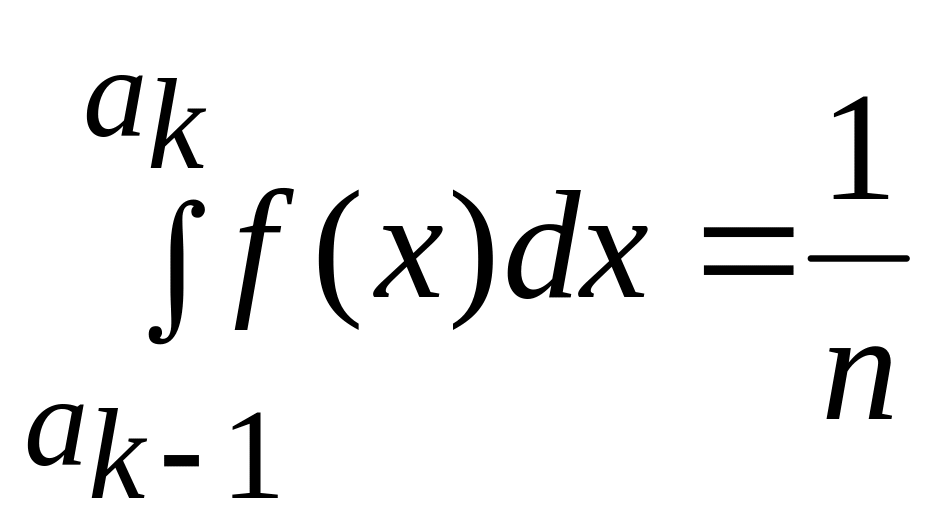Попадание случайной величины Y в любой частичный интервал можно рассматривать как событие, входящее в полную группу несовместных событий. А если случайная величина Y попадает в данный частичный интервал, то имеет на нем равномерное распределение.

Алгоритм моделирования.

Основные этапы моделирования.

1. С помощью датчика случайных чисел с равномерным распределением, вырабатывающего величину , моделируют дискретную случайную величину – номер интервала k.

2. Вторично разыгрывают случайную величину  и определяют возможное значение случайной величины Y при условии ее попадания в найденный интервал k:

, .

Схема алгоритма показана на рис. 4.

Способы построения моделирующих алгоритмов, организация квазипараллелизма

В зависимости от состава алгоритмов активностей, наличия связей между компонентами, целей и задач моделирования выбирается тот или иной способ представления компонент и реализации активностей в имитационных моделях.

Наиболее распространенные способы описания имитационной модели (формализации объекта моделирования):

• непосредственно активностями;

• аппаратом событий;

• транзактами;

• агрегатами;

• процессами.

Каждому способу формализации объекта моделирования соответствует свой способ организации квазипараллелизма обслуживания управляющей программой модели активностей, из которых составлена модель.

Наиболее распространенные способы организации квазипараллелизма в имитационной модели:

• просмотр активностей;

• составление расписания событий;

• управление обслуживанием транзактов;

• управление агрегатами;

• синхронизация процессов.

Одну и ту же сложную систему принципиально можно представить любым из указанных способов формализации, однако имитационные модели, построенные на их основе, будут отличаться размерами и количеством ресурсов, затрачиваемых на их создание, испытание и использование.

Описание активностями имитационной модели

Условия применения. Все функциональные действия компонент реальной системы различны, причем для выполнения каждого из них требуется выполнение своих условий. Эти условия конкретны, известны заранее исследователю и могут быть представлены алгоритмически. В результате выполнения функциональных действий в системе происходят различные события. Связи между функциональными действиями отсутствуют, все функциональные действия функционируют независимо друг от друга.

Состав имитационной модели:

• множество активностей ;

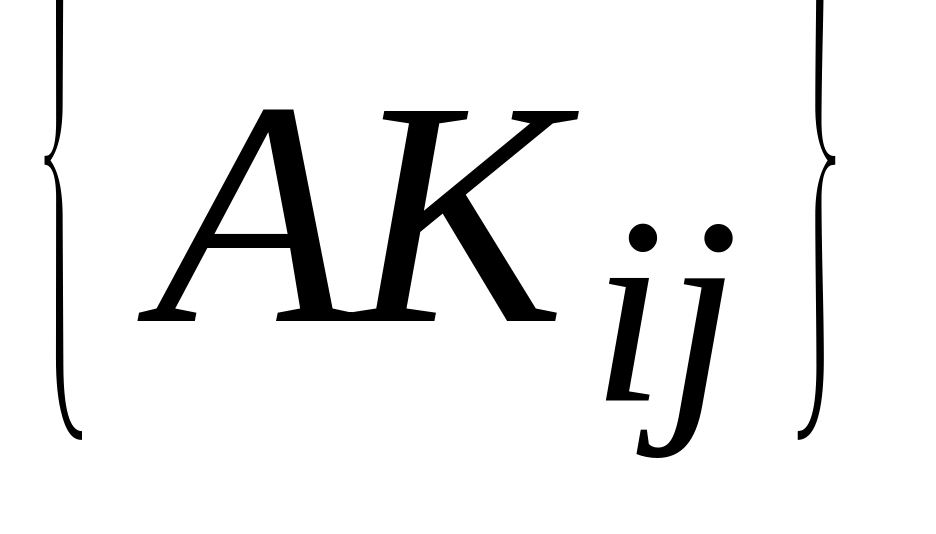• набор процедур проверки выполнимости условий инициализации активностей.

Инициализация активности – это передача управления от управляющей программы модели на выполнение алгоритма данной активности.

Процедура проверки выполнимости условий инициализации активностей – это процедура, в которой реализуется зависимость выполнения функционального действия от конкретной ситуации, имеющей место в реальной системе на каждый момент времени.

Обслуживание активности – это выполнение на ЭВМ алгоритма данной активности. Оно завершается выполнением оператора модификации временной координаты компоненты . По этому оператору управление возвращается управляющей программе модели.

Сущность имитации на ЭВМ при описании активностями. Имитация на ЭВМ представляет собой чередование выполнения алгоритмов активностей, операторов модификации временной координаты и алгоритма управляющей программы модели. Вся имитационная модель представляет собой набор активностей , каждая из которых после выполнения на ЭВМ возвращает управление управляющей программе модели.