Имитационное моделирование случайных величин с показательным распределением
Задача. Требуется смоделировать
случайную величину X,
имеющую показательное распределение,
задаваемое функцией распределения
,
где – параметр
распределения, с помощью случайной
величины с
равномерным распределением на отрезке
[0,1].
Принцип моделирования. Применив
метод обратной функции, получим =F(X)=
,
откуда
.
Учитывая, что случайная величина (1-)
имеет также равномерное распределение
на отрезке [0,1], окончательно имеем:
.
Имитационное моделирование случайных величин с равномерным распределением
Задача. Требуется смоделировать случайную величину X, имеющую равномерное распределение на отрезке [a,b], с помощью случайной величины с равномерным распределением на отрезке [0,1].
Принцип моделирования первым
способом. Применив метод обратной
функции, получим =F(X)=
,
откуда X=a+(b-a).
Принцип моделирования вторым
способом.
,
где
– среднее значение случайной величины
X,
.
Имитационное моделирование случайных величин с нормальным распределением
Задача. Требуется смоделировать случайную величину Y, имеющую нормальное распределение с математическим ожиданием M(Y) и среднеквадратическим отклонением (Y), с помощью случайной величины с равномерным распределением на отрезке [0,1].
Принцип моделирования. Метод обратной функции для имитационного моделирования нормально распределенной случайной величины неприменим, так как нельзя найти аналитическое выражение для нормальной функции. Вместо метода обратной функции используется центральная предельная теорема теории вероятностей, согласно которой при сложении достаточно большого числа одинаково распределенных независимых случайных чисел получается случайная величина, имеющая нормальное распределение. Как показали исследования, уже при сложении более десяти случайных величин с равномерным распределением на отрезке [0,1] получается случайная величина, которая с точностью, достаточной для большинства практических задач, может считаться распределенной нормально.
Процедура моделирования.
Сложим 12 взаимно независимых случайных величин с равномерным распределением на отрезке [0,1]:
.
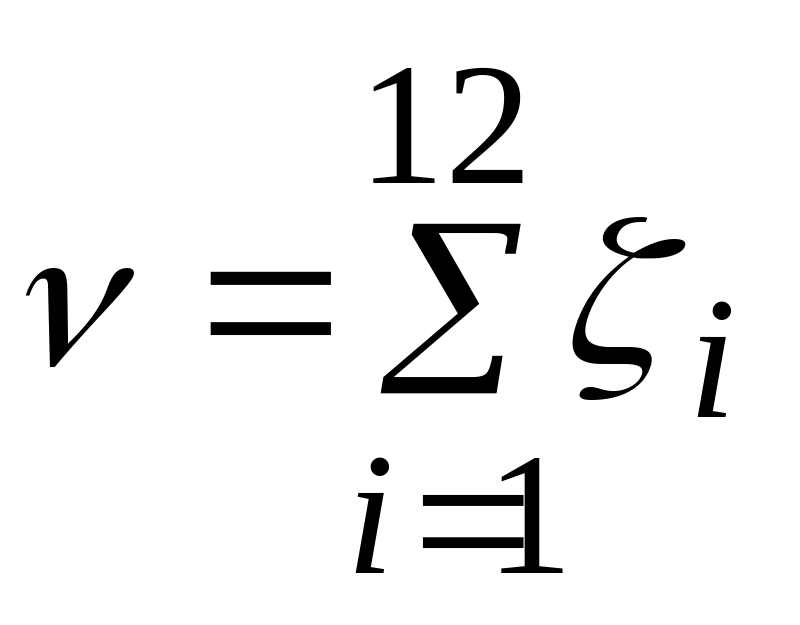Использовав известные теоремы о сумме
математических ожиданий и дисперсий
независимых случайных величин, можно
установить, что в данном случае случайная
величина имеет
математическое ожидание M()=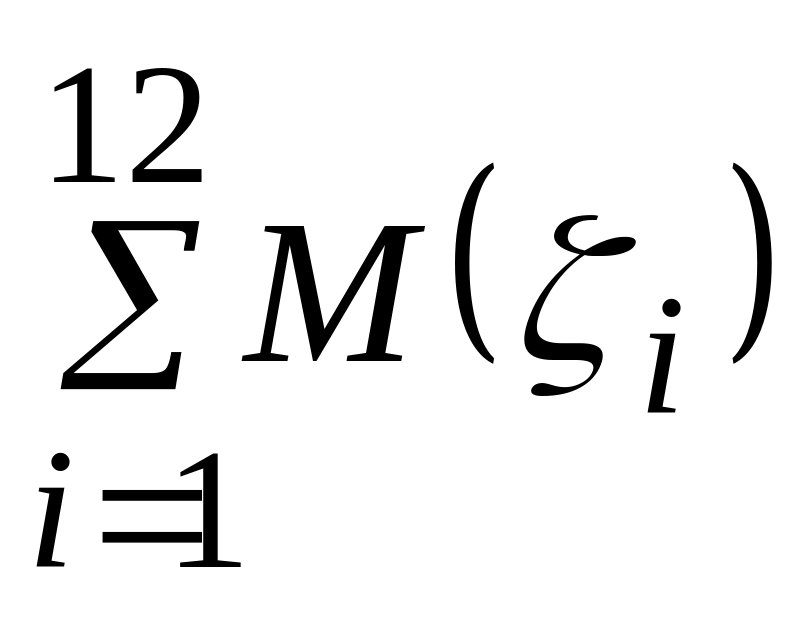
=
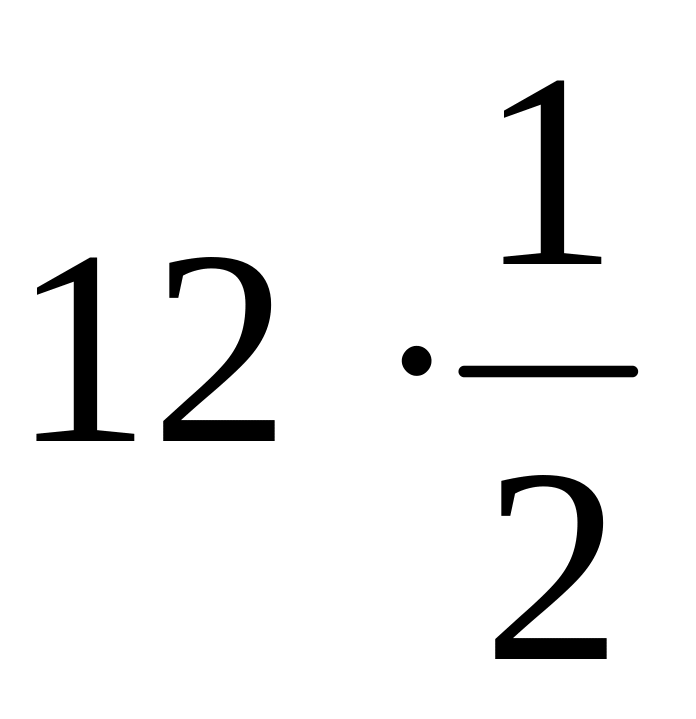=6,
дисперсию D()=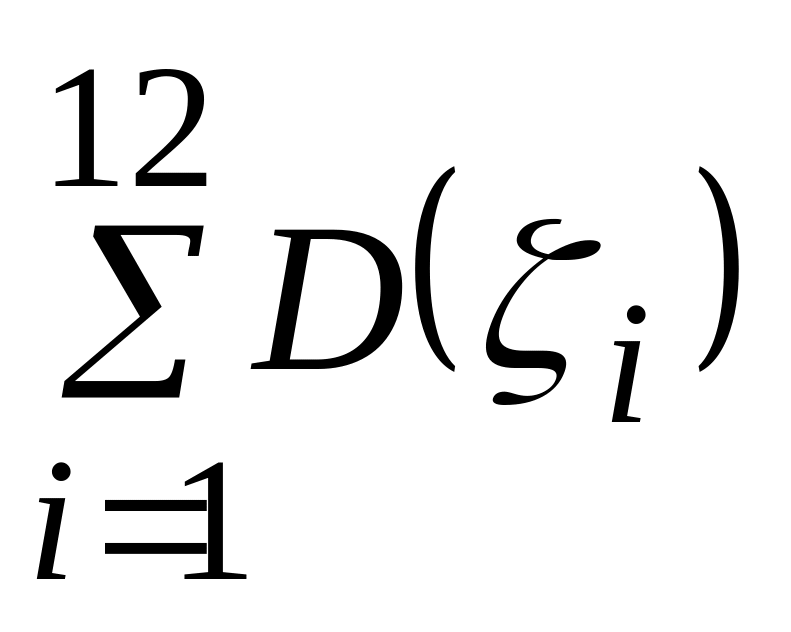
=
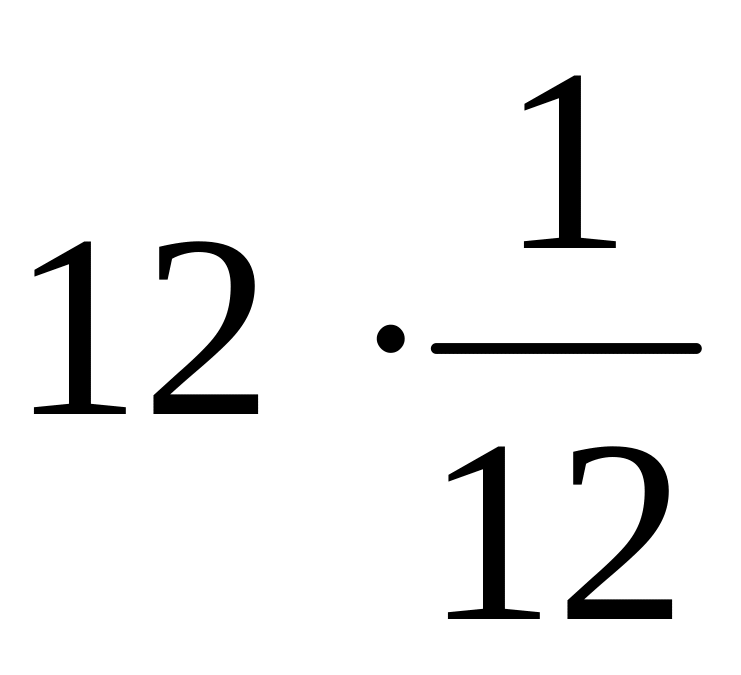=1
и среднеквадратическое отклонение
()=
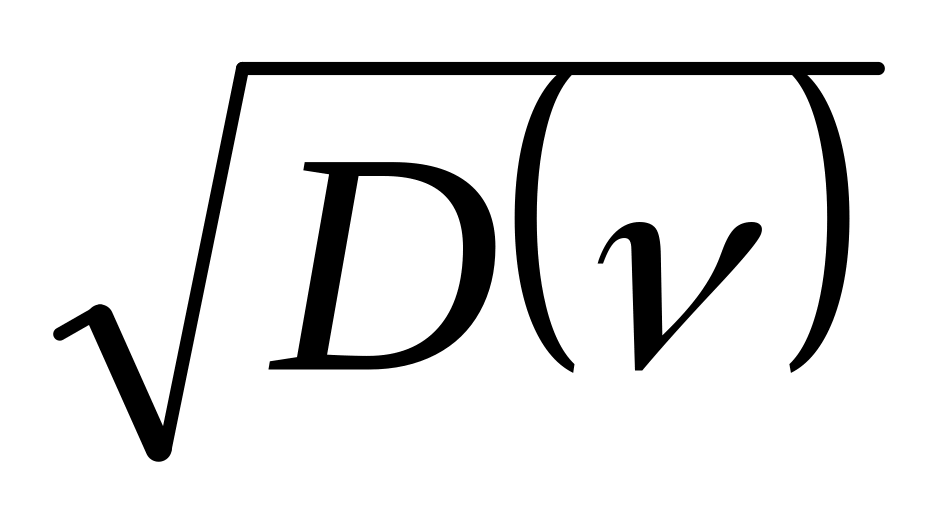=1.Нормируем и центрируем случайную величину , т.е. перейдем к величине =(—M())/()=—6.
От нормированной и центрированной случайной величины перейдем к искомой случайной величине Y:
.
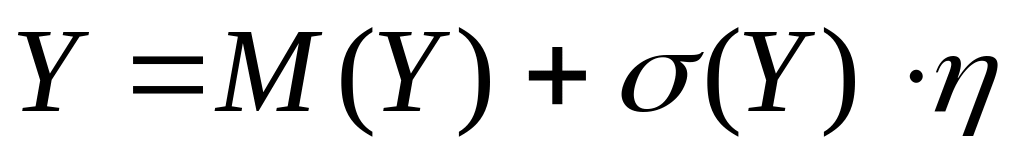Окончательно имеем:
.
Имитационное моделирование случайных величин с усеченным нормальным распределением
Понятие усеченного нормального распределения.
Параметры распределения:
математическое ожидание M(Y) нормального распределения;
среднеквадратическое отклонение (Y) нормального распределения;
максимальное и минимальное значения
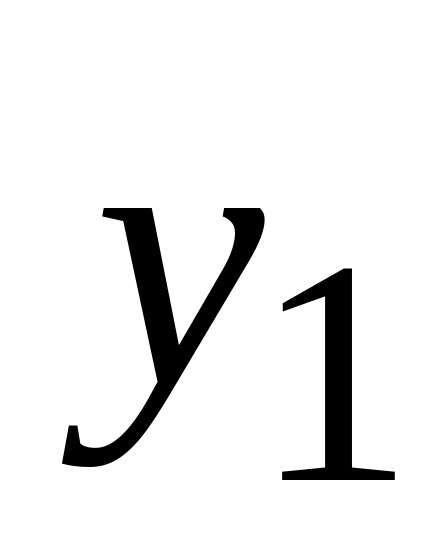и
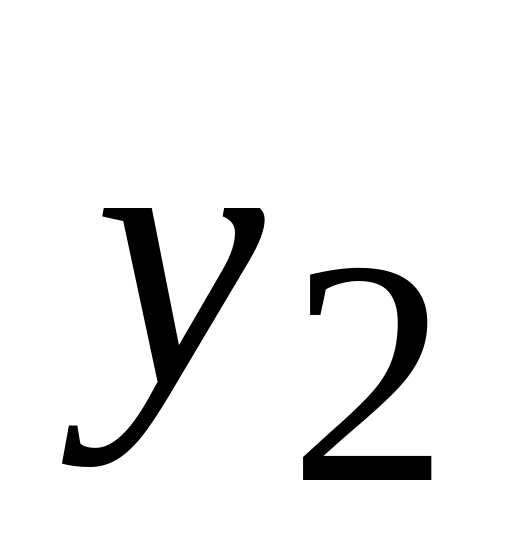(точки усечения).
Функция распределения:
где
;
;
;
.
Задача. Требуется смоделировать случайную величину Y, имеющую усеченное нормальное распределение с математическим ожиданием M(Y) нормального распределения, среднеквадратическим отклонением (Y) нормального распределения и точками усечения и , с помощью случайной величины с равномерным распределением на отрезке [0,1].
Принцип моделирования. Используется процедура имитационного моделирования нормального распределения и дополняется процедурой усечения.
Алгоритм моделирования.
Оператор 1 обращается к процедуре моделирования случайной величины Y, нормально распределенной с заданными параметрами M(Y) и (Y).
Оператор 2 проверяет условие попадания случайной величины Y в неусеченную область. При выполнении этого условия значение случайной величины Y с усеченным нормальным распределением считается найденным. В противном случае управление в алгоритме передается вновь на вход оператора 1, и генерируется другая случайная величина.
