Классификационные признаки смо

Характеристики входа СМО.

• Число заявок на входе (размер популяции): либо бесконечное (неограниченная популяция), либо конечное (ограниченная популяция).

• Режим поступления заявок в СМО: характеризуется параметрами входящего потока.

• Поведение клиентов: ограниченное или неограниченное время ожидания в очереди, возможность перехода из одной очереди в другую.

Характеристики очереди.

• Длина очереди: ограниченная или неограниченная.

• Правило обслуживания (характеризуется приоритетами обслуживания).

Характеристики процесса обслуживания.

• Структура СМО (состав СМО по числу каналов и числу фаз обслуживания, а также функциональные связи между ними).

• Режим обслуживания (характеризуется временем обслуживания заявки).

Характеристики качества (параметры моделей очередей) смо

Наиболее распространенные технические характеристики качества СМО.

• Среднее время, которое клиент проводит в очереди.

• Средняя длина очереди.

• Среднее время, которое клиент проводит в СМО (время ожидания плюс время обслуживания).

• Среднее число клиентов в СМО.

• Вероятность того, что СМО окажется незанятой.

• Вероятность определенного числа клиентов в СМО.

Наиболее распространенные экономические характеристики качества СМО.

• Издержки ожидания в очереди.

• Издержки ожидания в СМО.

• Издержки обслуживания.

Компактная запись математических моделей смо в форме Кендалла-Башарина

Применение. В научной литературе для компактной записи математических моделей СМО часто пользуются обозначениями, предложенными Д. Кендаллом, и модифицированными – Г.П. Башариным.

Структура. Математическую модель СМО обозначают последовательностью символов.

1. Первый символ обозначает функцию распределения промежутков между вызовами.

2. Второй символ обозначает функцию распределения длительности обслуживания.

3. Третий и последующие символы обозначают схему и дисциплину обслуживания.

Символика.

• M – показательный закон распределения.

• E – эрланговский закон распределения.

• D – детерминированная величина.

• G – произвольный закон распределения.

• (стрелка над символами) – многомерный случай.

• S – схема системы телетрафика.

• v – число линий (если схема представляет собой полнодоступный пучок линий, то вместо S пишется v).

• r – число мест для ожидания в очереди.

• f (с индексами) – обозначение приоритетов в обслуживании.

Примеры.

• M / M / S – схема S, на которую поступает поток с показательной функцией распределения промежутков между вызовами (простейший поток вызовов) и показательной функцией распределения длительности обслуживания.

• M / M / v< – полнодоступный пучок с конечным числом линий, который обслуживает с потерями простейший поток вызовов с показательной функцией распределения длительности обслуживания.

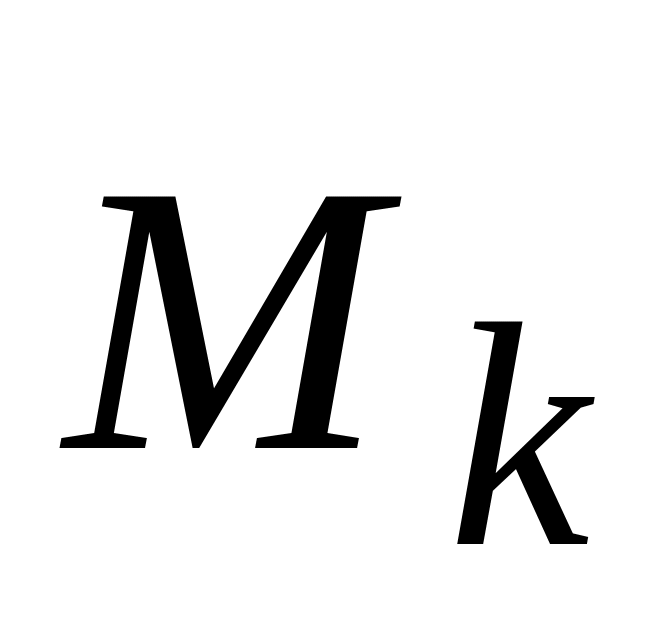• / / v / r< / – полнодоступный пучок из v линий, который обслуживает с ожиданием k потоков с показательными функциями распределения промежутков между вызовами; каждый поток имеет произвольную функцию распределения длительности обслуживания; число мест для ожидания r<; постановка вызовов в очередь осуществляется без приоритетов – , выборка из очереди – также без приоритетов – .