2.4.4. Расчет норм надежности

Под нормой надежности обычно понимается величина показателя надежности, подлежащая обеспечению (подтверждению расчетами и/или испытаниями). Норма надежности для изделия и его составных частей определяется при проработке требований по надежности, выдвинутых заказчиком в техническом задании, либо при эскизном проектировании. На норму надежности влияют как экономичность изделия, так и его безопасность (особенно в случае оборудования ЯЭУ).

Можно даже увидеть, что между этими двумя качествами есть диалектическое противоречие: из предыдущего материала этого раздела ясно, что увеличения надежности (а значит безопасности) можно достичь резервированием. Но оно требует определенных материальных затрат, т.е. снижает экономичность. Понятно также, например, что увеличение экономичности требует ужесточения режимов работы оборудования, а следовательно, уменьшения запасов до предельно-допустимых нагрузок, а это – снижение надежности, т.е., в конечном итоге, безопасности ЯЭУ. Есть оптимум между требованиями экономичности, надежности и безопасности. Хорошая ЯЭУ – это ЯЭУ, находящаяся в районе этого оптимума.

В нормативных документах регламентируются показатели НиБ ЯЭУ. В частности, в ОПБ-88/97 оговорены требования на вероятность предельного аварийного выброса р/а веществ (10^-7 в течение года) и вероятность тяжелого повреждения или плавления активной зоны (10^-5 в течение года). К надежности различного оборудования ЯЭУ (корпусам, ГЦН, СУЗ и др.) предъявляются требования в различных ГОСТах.

Допустим, установлена норма надежности на ЯЭУ в целом или на какую-либо ее систему. Встает вопрос: как эту норму разложить на надежность составляющих частей? Обычно норма надежности изделия устанавливается в виде вероятности безотказной работы Р(t) либо средней наработки на отказ  . Определение норм надежности для изделия и его элементов производится, как правило, с помощью упрощенных расчетов, основанных на следующих допущениях:

- закон изменения вероятности P(t) при внезапных отказах – экспоненциальный, т.е. опасность отказа (параметр потока отказов) изделий не зависит от времени;

- все элементы равнонадежны;

- все элементы включены последовательно.

Исходными данными при проведении расчетов являются:

а) количество N элементов расчета надежности (блоков, узлов, приборов, устройств и т.п.), входящих в изделие;

б) требуемое время исправной непрерывной работы t₀ с заданной вероятностью P_н(t₀)

Если задана вероятность безотказной работы изделия Р_н, то

Р_н ,

где Р_i – вероятность безотказной работы любого элемента расчета надежности. Считая все элементы одинаковыми по надежности, найдем

Р_i Р .

Или при экспоненциальном законе надежности

Р_i е ,

где  – допустимая опасность отказа для изделия.

Следовательно, максимально допустимая опасность отказа для элемента расчета надежности в среднем равна

_i = /N

Следует иметь в виду, что полученное значение _i, имеет лишь приближенное (оценочное) значение, позволяющее оценить возможности построения блоков без дополнительных средств увеличения надежности их компонентов. Для этого берут значение. _j, для каждого из n_i, компонентов, входящих в i-й блок, и определяют наличие неравенства

_i

В случае, если неравенство не выполняется, то следует рассмотреть различные способы увеличения надежности элементов (облегчение режимов работы, резервирование).

ГЛАВА 3.

МЕТОДЫ ВЫЧИСЛЕНИЯ ПОКАЗАТЕЛЕЙ

НАДЕЖНОСТИ И БЕЗОПАСНОСТИ ЯЭУ

3.1. Использование пуассоновского потока для анализа без(мало-)аварийного опыта испытаний и(или) эксплуатации оборудования ЯЭУ

Ввиду потенциальной опасности ядерных технологий все лица и организации, причастные к ним, принимают необходимые меры для того, чтобы обеспечить в максимальной степени уровни их надежности и безопасности. Поэтому крупные аварии и отказы оборудования с серьезными последствиями в ядерных технологиях крайне редки или не происходили вообще. С другой стороны, в отличие от массовых (например, компьютерных, авиационных и др.) технологий, в ядерных технологиях в значительной мере используются единичные экземпляры оборудования, специально предназначенные для безотказного выполнения специфических для этого рода деятельности работы и/или технологических операций в течение длительного времени. Например, корпусы реакторов с водой под давлением, некоторые приводы органов СУЗ и др. изготавливаются в единичных экземплярах и предназначены для безотказного выполнения своих функций в течение десятков лет. Другой пример. Операции по перегрузкам ТВС в ЯР проводятся со специальными мерами предосторожности, чтобы избежать различные потенциальные опасности, например, такие как падение ТВС в активную зону или хранилище, чрезмерные перекосы ТВС в направляющих в процессе движения и т.п. Хотя эти операции, в принципе, носят массовый характер, тем не менее реализации подобных опасностей, приведшие к повреждению ТВС, – крайне редкие события. Третий пример. В отличие от массовых перевозок обычных грузов (угля, нефти, строительных и других материалов) перевозки по железным дорогам контейнеров с ТВС между ЯЭУ и заводами по их изготовлению или переработке, а также единичных экземпляров корпусов ЯЭУ от места изготовления до полигона, являются уникальными операциями со специально принятыми мерами предосторожности, обеспечивающими в максимальной степени их безопасность и делающими транспортные аварии (ТА) с такими объектами крайне маловероятными. Поэтому при оценках количественных характеристик НиБ для ядерных технологий часто возникают трудности, связанные с тем, что такие оценки необходимо проводить для уникальных объектов и операций, отказы и/или аварии которых происходили редко или не происходили вообще.

Принципиальная позиция автора состоит в том, что безаварийный опыт эксплуатации уникальных объектов и/или проведения уникальных операций в ядерных технологиях – это тоже опыт, который необходимо и возможно использовать при оценках количественных характеристик их НиБ. Оказывается, что можно построить простые, основанные на здравом смысле и разумном консерватизме, вероятностные модели, учитывающие важнейшие особенности режимов эксплуатации, ремонтов и обслуживания уникальных объектов и(или) проведения уникальных операций, дающие возможность получать обоснованные и консервативные оценки параметров НиБ, а также оценивать вероятностные характеристики возможных, но нереализовавшихся причин отказов или аварий. Далее приведена простая вероятностная модель, позволяющая оценивать не только требуемые показатели НиБ, но также и достаточность имеющегося без(мало-)аварийного опыта для уверенного суждения о НиБ изучаемых объектов и операций.

Для построения модели необходимо выдвинуть ряд предположений о характере изучаемых явлений. Коль скоро здесь речь идет об уникальных, очень надежных объектах и без(мало-)аварийном опыте их эксплуатации, то первое предположение, которое разумно сделать, состоит в том, что отказы таких объектов – очень редкие события, поток которых должен хорошо описываться распределением Пуассона.

К результатам наблюдения потока редких событий, т.е. к 6ез(мало-)аварийному опыту, необходимо относиться с определенной долей скептицизма в связи с двумя вполне очевидными обстоятельствами.

1. Имеющийся без(мало-)аварийный опыт может оказаться результатом "везения", т.е. из-за случайной группировки очень редких событий их оказалось меньше, чем должно в среднем наблюдаться в интервале времени наблюдения.

2. Очень надежные объекты, как правило, одновременно являются и очень ответственными, например, системами или элементами, важными для безопасности, за отказы которых, происшедшие по его вине, эксплуатационный персонал несет ответственность. Следовательно, даже если в соответствующей документации зафиксировано мало отказов, по-видимому, следует учитывать возможность того, что отказов было на самом деле, по крайней мере, на один больше, но они не все зафиксированы.

Таким образом, вторым, предположением, которое разумно сделать, должно быть следующее: наблюденный без(мало-)аварийный опыт является результатом маловероятного "счастливого" события, на самом деле с большой вероятностью отказов должно быть, по крайней мере, на один больше, но нам повезло. Это предположение обеспечит консервативность оценок надежности, т.к. априори всегда завышает наблюденную (зафиксированную) статистику по отказам (авариям).

В соответствии с первым предположением распределение числа k отказов (аварий) на интервале времени наблюдения t принимает вид

P_k (t) = exp (– , (3.1)

где (t) – ведущая функция потока отказов, подлежащая оценке. Эту функцию в зависимости от существа задачи можно задать для последующих оценок двумя способами.

1. Если речь идет о непрерывной эксплуатации объекта в течение времени t, то

(t) = t,

где – средний на интервале [0, t] параметр потока отказов.

2. Если речь идет о проведенных п операциях с объектом на интервале времени t, то

(t) = nр,

где р – вероятность того, что одна операция окажется неудачной, например, закончится аварией.

Во втором случае формулу (3.1) удобно переписать в виде

P_k,n = exp(–np), (3.2)

Допустим, в результате наблюдения за объектом принято решение, что он отказывал на интервале времени t ровно j  0 раз. Тогда вероятность того, что на этом интервале отказов объекта было хотя бы на один больше, есть

P_ = exp(– , (3.3)

В случае п операций эта вероятность записывается в виде

P_ = exp(­–np). (3.4)

Если задать значение вероятности Р_ , то при заданном j можно решить уравнения (3.3) или (3.4) относительно неизвестных (t) или р. В соответствии со вторым предположением вероятность Р_ следует задавать достаточно большой, например, принять Р_ = 0.9. Тогда решения или записанных уравнений будут верхними пределами интервалов [0, ] и

[0, ] соответственно, в которых с большой доверительной вероятностью Р_ лежат истинные значения (t) и р.

Здесь уместно обсудить смысл вероятности Р_ более подробно. С одной стороны, как отмечено, это доверительная вероятность для числовых оценок, а с другой – она отражает степень недоверия к наблюденному без (мало-) аварийному опыту. Чем больше а = 1 – Р_ , тем большее предпочтение отдается гипотезе о том, что без (мало-)аварийный опыт эксплуатации объекта (проведения операций с объектом) не является результатом "везения", а предопределен адекватностью принимаемых мер по обеспечению надежной эксплуатации объекта или безопасному проведению операций с ним. Соответственно тем меньше отдается шансов противоположной гипотезе о том, что хотя бы на один отказ (на одну аварию) должно было произойти больше, но или нам "повезло", или остальные инциденты просто не зафиксированы (по халатности или умышленно). Выбрав Р_α = 0.5, мы не отдаем предпочтения ни одной из этих двух гипотез, т.е. равно доверяем и не доверяем без(мало-)аварийному опыту. Следовательно, такое значение Р_α дает возможность оценивать некие "средневероятные" величины (t) или т.е. получать точечные оценки (t), р внутри интервалов [0, ] и [0, _n].

Особый интерес представляют оценки при j = 0, т.е. когда имеется чисто безаварийный опыт эксплуатации объекта или проведения операций с ним. В этом случае с помощью формул

(t) = – , (3.5)

, (3.6)

где тильда над параметром означает предельную или средневероятную оценку, оцениваются вероятностные характеристики событий, которые ни разу не наблюдались на практике. Следовательно, как бы ни было сформулировано понятие отказа объекта, при заданных t, n, Р_ и j = 0 мы в любом случае, получим одни и те же оценки и . В связи с этим, можно заподозрить элементы схоластики в изложенном подходе.

Однако, если проведен серьезный инженерный анализ возможных, но не реализовавшихся, причин отказов объекта и понятие отказа сформулировано при четком учете функций, выполняемых объектом, и возможных механизмов его повреждения для реальных условий эксплуатации, обслуживания и ремонтов, то оценки будут проведены не для надуманных, абстрактных событий, а для реально представляющих потенциальную опасность, но не реализовавшихся в период наблюдения за объектом. Таким образом, инженерный анализ и формулировка на его основе возможного отказа объекта, который на практике ни разу не отказывал, является составной частью анализа безаварийного опыта эксплуатации. Чисто статистический подход при таком анализе может приводить к недоразумениям, т.к. вероятностные методы - всего лишь инструмент для вычислений в вероятностном пространстве, которое задается только на основе инженерного (физического) анализа изучаемых явлений.

Обычно при инженерном анализе без (мало-)аварийного опыта можно выдвинуть несколько гипотез относительно причин отказов и/или аварий (потенциальных опасностей), которые могли бы реализоваться, но не произошли. Например, при перевозках корпуса ЯЭУ по железным дорогам реальную потенциальную опасность для спецвагона представляют сход со стрелки, падение с моста, столкновение со встречным поездом на однопутном участке маршрута и т.п. Ясно, что оценки вероятностных характеристик таких реальных потенциальных опасностей по имеющемуся без (мало-)аварийному опыту их прохождения могут представлять практический интерес, т.к. дают возможность переносить полученный опыт на новые объекты (маршруты) и/или определять иерархию опасностей по их вероятностям для принятия решений о первоочередных мерах по поддержанию НиБ изучаемых объектов.

На примере анализа безаварийного опыта проведения n операций с объектом, для которого определены т опасностей, покажем как можно получить взаимосогласованные по степени доверия оценки вероятностных характеристик каждой из опасностей. В этом случае сделанные по формуле (3.6) оценки и вероятности р необходимо распределить на каждую выделенную опасность, т.е. провести верхнюю _n,j и средневероятную _n,j оценки вероятностей q_i (i = ) причин аварий с объектом. Это можно сделать следующим образом.

С одной стороны, очевидно, что

,

а с другой, следуя логике, изложенной выше,

где Р_,i – доверительная вероятность для оценки _n,i вероятности q_i реализации i-й опасности. Допустим, нет оснований оказывать предпочтительное доверие какой-либо из оценок _n,i . Тогда Р_,i = Р_ и после всех алгебраических преобразований можно получить для достаточно большого n (большого числа наблюдений безаварийного опыта)

P_ = 1– (1 – 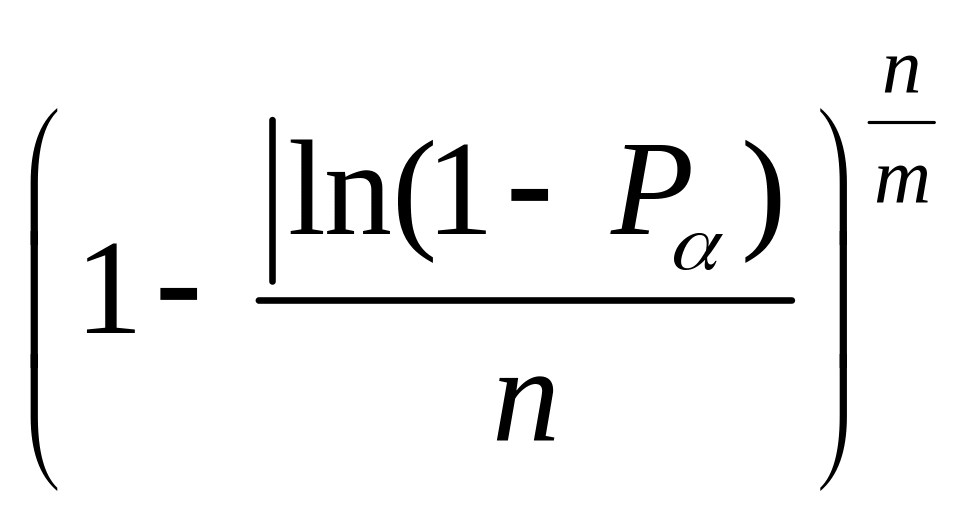. (3.7)

Таким образом, выбирая Р_ в соответствии с последним выражением, можно получить согласованные с наблюденным опытом и взаимосогласованные (по степени доверия) вероятностные характеристики различных опасностей для анализируемой операции. Из формулы (3.7) видно: при фиксированном числе наблюдений п, чем больше число m > 1 опасностей, по которым требуется распределить величину , тем меньше Р_ < Р_ , т.е. тем больше шансов, которые определяются вероятностью

 = 1-Р_ , отдается предположению, что наблюденный безаварийный опыт для каждый отдельной опасности не является "счастливой" случайностью. Из изложенного также следует, что оценки вероятностей q_i , различных опасностей одни и те же и равны

_n = 1 – G^1/m.

В случае, когда принимается Р_ = 0.5, проводятся средневероятные оценки и при m > 1 Р_ < 0.5. То есть парциальные (для отдельных опасностей), точечные, средневероятные для всего безаварийного опыта оценки вычисляются при меньшей, чем 0.5, вероятности недоверия к нему. С увеличением числа наблюдений (n), как видно из формулы (3.7),

P_  1 – (1 – P_)^1/m. (3.8)

Таким образом, с увеличением числа безаварийных наблюдений вероятность P_ как величина, характеризующая степень недоверия к ним для каждой отдельной опасности, уменьшается. Она стремится к пределу, определяемому вероятностью P_ , которая характеризует степень недоверия к опыту безаварийного прохождения всей совокупности опасностей для анализируемой операции.

При анализе безаварийного опыта проведения операций с объектами ядерных технологий всегда остается актуальным вопрос: является ли этот опыт достаточным для уверенного суждения о безопасности таких операций. Из анализа зависимости Р_ (n) можно получить на него ответ. Под достаточностью здесь понимается следующее. Получаемые по всем приведенным формулам оценки вероятностных характеристик опасностей обратно пропорциональны числу наблюдений n и с ростом числа безаварийных операций уменьшаются. Однако степень доверия к этим оценкам Р_ после определенного числа опытов приближается к некоторому значению, и сколь угодно большое увеличение числа опытов существенно изменить ее не может. Тогда можно говорить, что число опытов (при заданной доверительной вероятности P_) достаточно для суждения о вероятностных характеристиках отдельных опасностей и принятия решения о безопасности при проведении следующей операции.

На рис. 3.1. приведены результаты расчетов по формуле (3.7) зависимости Р_ от числа операций n для трех значений P_ и

т = 5. Из него видно, что, например, для P_= 0.9 в интервале значений n от 1 до 50 вероятность Р_ недоверия к безаварийному опыту проведения операций резко уменьшается, а затем достаточно полого стремится к предельному при n значению Р_ = 0.369, определяемому формулой (3.8).

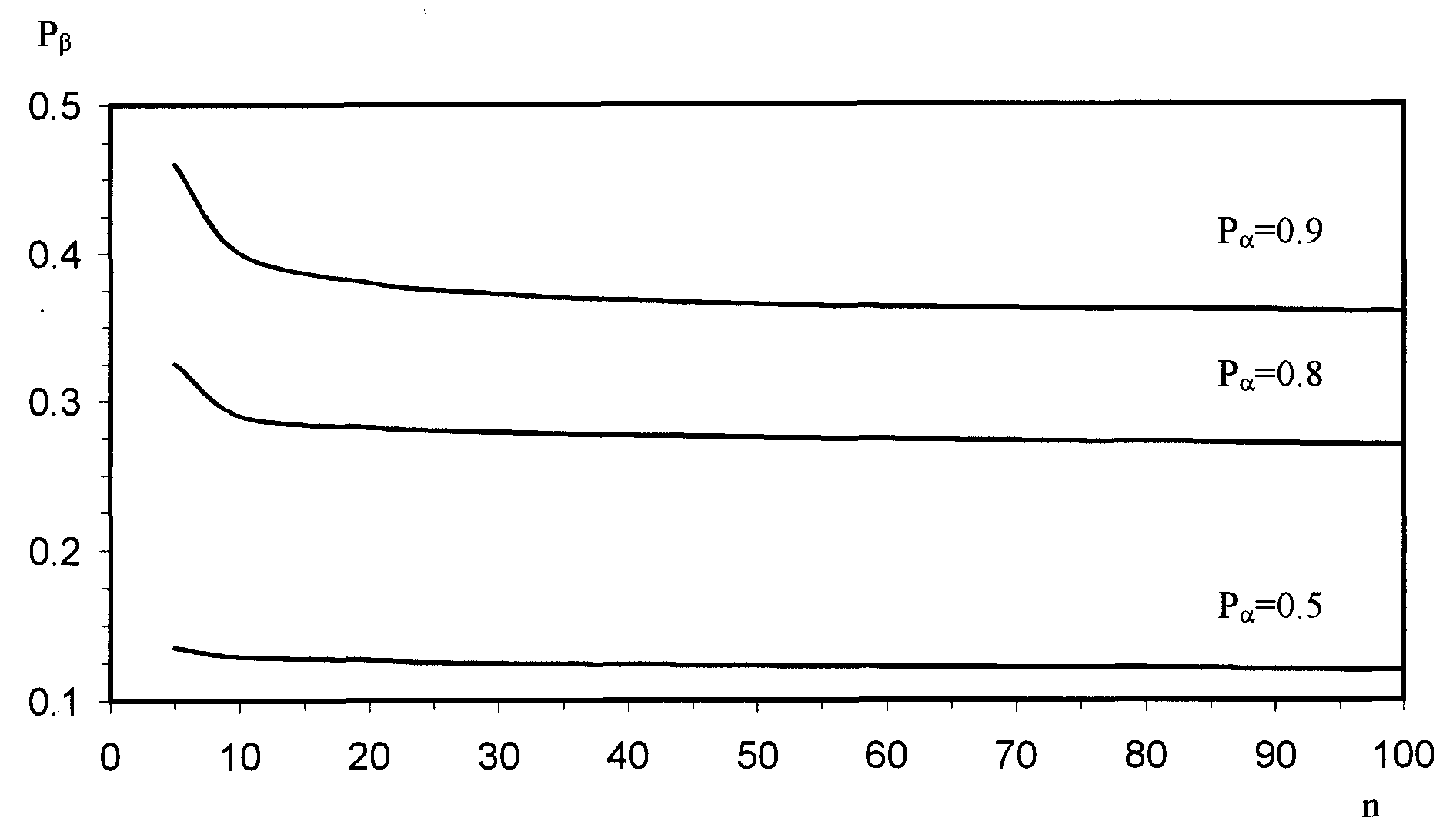
Рис. 3.1. Зависимость парциальной доверительной вероятности Р_ от объема n безаварийного опыта прохождения опасностей

В случае оценок показателей надежности оборудования ЯЭУ по безаварийному опыту эксплуатации, т.е. оценок параметра потока отказов по формуле (3.5), требуется выносить суждение о достаточности этого опыта в течение времени t_наб для уверенного суждения о надежности объекта в течение последующего периода t_прог. Понятно, что, когда период t_прог сравним с интервалом наблюдения t_наб или даже больше него, то о достаточности опыта не имеет смысла говорить. Только в случае, когда

t_прог << t_наб, т.е. когда период, на который требуется сделать прогноз, много меньше времени наблюдения безаварийного опыта, возможно вынести суждение о его достаточности. Приведенные формулы (3.7) и (3.8), на основе которых делаются соответствующие оценки, и в этом случае остаются в силе. Только в качестве п здесь следует принимать целое от отношения t_наб / t_прог , т.е. в этом случае n – кратность времени наблюдения безаварийного опыта к периоду прогноза на будущее.